13.1 INTRODUCTION
The first recording of the electric field of the human brain was made by the German psychiatrist Hans Berger in 1924 in Jena. He gave this recording the name electroencephalogram (EEG). (Berger, 1929).(From 1929 to 1938 he published 20 scientific papers on the EEG under the same title "Über das Elektroenkephalogram des Menschen".) The electric activity of the brain is usually divided into three categories:
The electric activity of the brain is usually divided into three categories:
1. spontaneous activity,
2. evoked potentials, and
3. bioelectric events produced by single neurons.
The number of nerve cells in the brain has been estimated to be on the order of 1011. Cortical neurons are strongly interconnected. Here the surface of a single neuron may be covered with 1,000-100,000 synapses (Nunez, 1981). The electric behavior of the neuron corresponds to the description of excitable cells introduced in the earlier chapters. The resting voltage is around -70 mV, and the peak of the action potential is positive. The amplitude of the nerve impulse is about 100 mV; it lasts about 1 ms.
 Spontaneous activity is measured on the scalp or on the brain and is called the electroencephalogram. The amplitude of the EEG is about 100 µV when measured on the scalp, and about 1-2 mV when measured on the surface of the brain. The bandwidth of this signal is from under 1 Hz to about 50 Hz, as demonstrated in Figure 13.1. As the phrase "spontaneous activity" implies, this activity goes on continuously in the living individual.
Spontaneous activity is measured on the scalp or on the brain and is called the electroencephalogram. The amplitude of the EEG is about 100 µV when measured on the scalp, and about 1-2 mV when measured on the surface of the brain. The bandwidth of this signal is from under 1 Hz to about 50 Hz, as demonstrated in Figure 13.1. As the phrase "spontaneous activity" implies, this activity goes on continuously in the living individual.
 Evoked potentials are those components of the EEG that arise in response to a stimulus (which may be electric, auditory, visual, etc.) Such signals are usually below the noise level and thus not readily distinguished, and one must use a train of stimuli and signal averaging to improve the signal-to-noise ratio.
Evoked potentials are those components of the EEG that arise in response to a stimulus (which may be electric, auditory, visual, etc.) Such signals are usually below the noise level and thus not readily distinguished, and one must use a train of stimuli and signal averaging to improve the signal-to-noise ratio.
 Single-neuron behavior can be examined through the use of microelectrodes which impale the cells of interest. Through studies of the single cell, one hopes to build models of cell networks that will reflect actual tissue properties.
Single-neuron behavior can be examined through the use of microelectrodes which impale the cells of interest. Through studies of the single cell, one hopes to build models of cell networks that will reflect actual tissue properties.
13.2 THE BRAIN AS A BIOELECTRIC GENERATOR
PRECONDITIONS:
SOURCE: Distribution of impressed current source elements  i (volume source)
i (volume source)
CONDUCTOR: Finite, inhomogeneous
 The bioelectric impressed current density
The bioelectric impressed current density  i associated with neuronal activation produces an electric field, which can be measured on the surface of the head or directly on the brain tissue. The electric field was described by Equation 7.10 for a finite inhomogeneous model. This equation is repeated here:
i associated with neuronal activation produces an electric field, which can be measured on the surface of the head or directly on the brain tissue. The electric field was described by Equation 7.10 for a finite inhomogeneous model. This equation is repeated here:
  | (13.01) |
 While for most excitable tissue the basis for the impressed current density
While for most excitable tissue the basis for the impressed current density  i is the propagating action potential, for the EEG it appears to arise from the action of a chemical transmitter on postsynaptic cortical neurons. The action causes localized depolarization - that is, an excitatory postsynaptic potential (EPSP) - or hyperpolarization - that is, an inhibitory postsynaptic potential (IPSP). The result in either case is a spatially distributed discontinuity in the function σΦ (i.e., σoΦo - σiΦi) which, as pointed out in Equation 8.28, evaluates a double layer source in the membranes of all cells. This will be zero for resting cells; however, when a cell is active by any of the aforementioned processes (in which case Φo - Φi = Vm varies over a cell surface), a nonzero primary source will result.
i is the propagating action potential, for the EEG it appears to arise from the action of a chemical transmitter on postsynaptic cortical neurons. The action causes localized depolarization - that is, an excitatory postsynaptic potential (EPSP) - or hyperpolarization - that is, an inhibitory postsynaptic potential (IPSP). The result in either case is a spatially distributed discontinuity in the function σΦ (i.e., σoΦo - σiΦi) which, as pointed out in Equation 8.28, evaluates a double layer source in the membranes of all cells. This will be zero for resting cells; however, when a cell is active by any of the aforementioned processes (in which case Φo - Φi = Vm varies over a cell surface), a nonzero primary source will result.
 For distant field points the double layer can be summed up vectorially, yielding a net dipole for each active cell. Since neural tissue is generally composed of a very large number of small, densely packed cells, the discussion in Section 8.5 applies, leading to the identification of a continuous volume source distribution
For distant field points the double layer can be summed up vectorially, yielding a net dipole for each active cell. Since neural tissue is generally composed of a very large number of small, densely packed cells, the discussion in Section 8.5 applies, leading to the identification of a continuous volume source distribution  i which appears in Equations 7.6 and 7.10.
i which appears in Equations 7.6 and 7.10.
 Although in principle the EEG can be found from the evaluation of Equation 7.10, the complexity of brain structure and its electrophysiological behavior have thus far precluded the evaluation of the source function
Although in principle the EEG can be found from the evaluation of Equation 7.10, the complexity of brain structure and its electrophysiological behavior have thus far precluded the evaluation of the source function  i. Consequently, the quantitative study of the EEG differs from that of the ECG or EMG, in which it is possible to evaluate the source function. Under these conditions the quantitative EEG is based on a statistical treatment, whereas the clinical EEG is largely empirical..
i. Consequently, the quantitative study of the EEG differs from that of the ECG or EMG, in which it is possible to evaluate the source function. Under these conditions the quantitative EEG is based on a statistical treatment, whereas the clinical EEG is largely empirical..

Fig. 13.1. Frequency spectrum of normal EEG.
13.3 EEG LEAD SYSTEMS
The internationally standardized 10-20 system is usually employed to record the spontaneous EEG. In this system 21 electrodes are located on the surface of the scalp, as shown in Figure 13.2A and B. The positions are determined as follows: Reference points are nasion, which is the delve at the top of the nose, level with the eyes; and inion, which is the bony lump at the base of the skull on the midline at the back of the head. From these points, the skull perimeters are measured in the transverse and median planes. Electrode locations are determined by dividing these perimeters into 10% and 20% intervals. Three other electrodes are placed on each side equidistant from the neighboring points, as shown in Figure 13.2B (Jasper, 1958; Cooper, Osselton, and Shaw, 1969). In addition to the 21 electrodes of the international 10-20 system, intermediate 10% electrode positions are also used. The locations and nomenclature of these electrodes are standardized by the American Electroencephalographic Society (Sharbrough et al., 1991; see Figure 13.2C). In this recommendation, four electrodes have different names compared to the 10-20 system; these are T7, T8, P7, and P8. These electrodes are drawn black with white text in the figure.
In addition to the 21 electrodes of the international 10-20 system, intermediate 10% electrode positions are also used. The locations and nomenclature of these electrodes are standardized by the American Electroencephalographic Society (Sharbrough et al., 1991; see Figure 13.2C). In this recommendation, four electrodes have different names compared to the 10-20 system; these are T7, T8, P7, and P8. These electrodes are drawn black with white text in the figure.
 Besides the international 10-20 system, many other electrode systems exist for recording electric potentials on the scalp. The Queen Square system of electrode placement has been proposed as a standard in recording the pattern of evoked potentials in clinical testings (Blumhardt et al., 1977).
Besides the international 10-20 system, many other electrode systems exist for recording electric potentials on the scalp. The Queen Square system of electrode placement has been proposed as a standard in recording the pattern of evoked potentials in clinical testings (Blumhardt et al., 1977).
 Bipolar or unipolar electrodes can be used in the EEG measurement. In the first method the potential difference between a pair of electrodes is measured. In the latter method the potential of each electrode is compared either to a neutral electrode or to the average of all electrodes (see Figure 13.3).
Bipolar or unipolar electrodes can be used in the EEG measurement. In the first method the potential difference between a pair of electrodes is measured. In the latter method the potential of each electrode is compared either to a neutral electrode or to the average of all electrodes (see Figure 13.3).
 The most recent guidelines for EEG-recording are published in (Gilmore, 1994).
The most recent guidelines for EEG-recording are published in (Gilmore, 1994).


Fig. 13.2. The international 10-20 system seen from (A) left and (B) above the head. A = Ear lobe, C = central, Pg = nasopharyngeal, P = parietal, F = frontal, Fp = frontal polar, O = occipital.
(C) Location and nomenclature of the intermediate 10% electrodes, as standardized by the American Electroencephalographic Society. (Redrawn from Sharbrough, 1991.).

Fig. 13.3. (A) Bipolar and (B) unipolar measurements. Note that the waveform of the EEG depends on the measurement location.
13.4 SENSITIVITY DISTRIBUTION OF EEG ELECTRODES
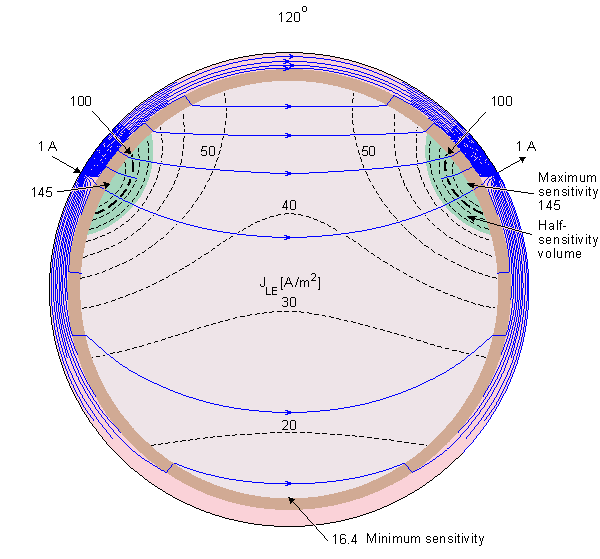
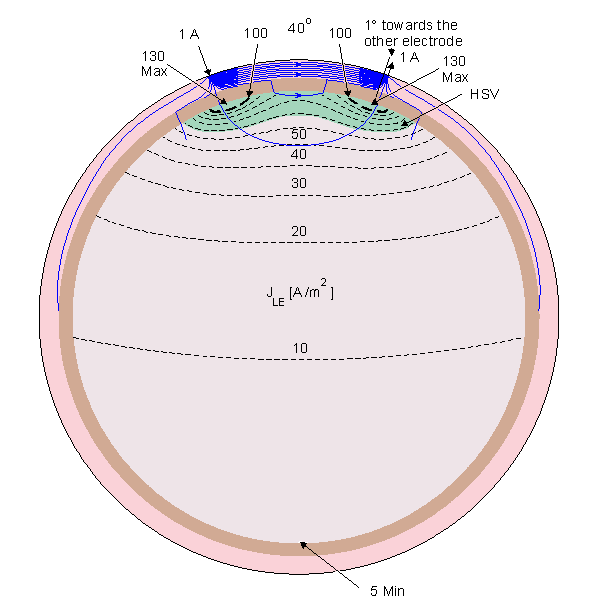
Rush and Driscoll (1969) calculated the sensitivity distribution of bipolar surface electrodes on the scalp based on a concentric spherical head model. They published the results in the form of lead field isopotential lines. The direction of the lead field current density - that is, the direction of the sensitivity - is a negative gradient of the potential field. This is not immediately evident from such a display. Puikkonen and Malmivuo (1987) recalculated the sensitivity distribution of EEG electrodes with the same model as Rush and Driscoll, but they presented the results with the lead field current flow lines instead of the isopotential lines of the lead field. This display is illustrative since it is easy to find the direction of the sensitivity from the lead field current flow lines. Also the magnitude of the sensitivity can be seen from the density of the flow lines. A minor problem in this display is that because the lead field current distributes both in the plane of the illustration as well as in the plane normal to it, part of the flow lines must break in order to illustrate correctly the current density with the flow line density in a three-dimensional problem. Suihko, Malmivuo and Eskola (1993) calculated further the isosensitivity lines and the half-sensitivity volume for the electric leads. As discussed in Section 11.6.1, the concept half-sensitivity volume denotes the area where the lead field current density is at least one half from its maximum value. Thus this concept is a figure of merit to describe how concentrated the sensitivity distribution of the lead is. As discussed in Section 11.6.6, when the conductivity is isotropic, as it is in this head model, the isosensitivity lines equal to the isofield lines of the (reciprocal) electric field. If the lead would exhibit such a symmetry that adjacent isopotential surfaces would be a constant distance apart, the isosensitivity lines would coincide with the isopotential lines. That is not the case in the leads of Figure 13.4.
Puikkonen and Malmivuo (1987) recalculated the sensitivity distribution of EEG electrodes with the same model as Rush and Driscoll, but they presented the results with the lead field current flow lines instead of the isopotential lines of the lead field. This display is illustrative since it is easy to find the direction of the sensitivity from the lead field current flow lines. Also the magnitude of the sensitivity can be seen from the density of the flow lines. A minor problem in this display is that because the lead field current distributes both in the plane of the illustration as well as in the plane normal to it, part of the flow lines must break in order to illustrate correctly the current density with the flow line density in a three-dimensional problem. Suihko, Malmivuo and Eskola (1993) calculated further the isosensitivity lines and the half-sensitivity volume for the electric leads. As discussed in Section 11.6.1, the concept half-sensitivity volume denotes the area where the lead field current density is at least one half from its maximum value. Thus this concept is a figure of merit to describe how concentrated the sensitivity distribution of the lead is. As discussed in Section 11.6.6, when the conductivity is isotropic, as it is in this head model, the isosensitivity lines equal to the isofield lines of the (reciprocal) electric field. If the lead would exhibit such a symmetry that adjacent isopotential surfaces would be a constant distance apart, the isosensitivity lines would coincide with the isopotential lines. That is not the case in the leads of Figure 13.4.
 Figure 13.4 displays the lead field current flow lines, isosensitivity lines and half-sensitivity volumes for the spherical head model with the electrodes located within 180°, 120°, 60°, 40°, and 20° angles. Note that in each case the two electrodes are connected with 10 continuous lead field flow lines. Between them are three flow lines which are broken from the center, indicating that the lead field current distributes also in the plane normal to the paper. The figure shows clearly the strong effect of the poorly conducting skull to the lead field. Though in a homogeneous model the sensitivity would be highly concentrated at the electrodes, in the 180° case the skull allows the sensitivity to be very homogeneously distributed throughout the brain region. The closer the electrodes are to each other, the smaller the part of the sensitivity that locates within the brain region. Locating the electrodes closer and closer to each other causes the lead field current to flow more and more within the skin region, decreasing the sensitivity to the brain region and increasing the noise.
Figure 13.4 displays the lead field current flow lines, isosensitivity lines and half-sensitivity volumes for the spherical head model with the electrodes located within 180°, 120°, 60°, 40°, and 20° angles. Note that in each case the two electrodes are connected with 10 continuous lead field flow lines. Between them are three flow lines which are broken from the center, indicating that the lead field current distributes also in the plane normal to the paper. The figure shows clearly the strong effect of the poorly conducting skull to the lead field. Though in a homogeneous model the sensitivity would be highly concentrated at the electrodes, in the 180° case the skull allows the sensitivity to be very homogeneously distributed throughout the brain region. The closer the electrodes are to each other, the smaller the part of the sensitivity that locates within the brain region. Locating the electrodes closer and closer to each other causes the lead field current to flow more and more within the skin region, decreasing the sensitivity to the brain region and increasing the noise.
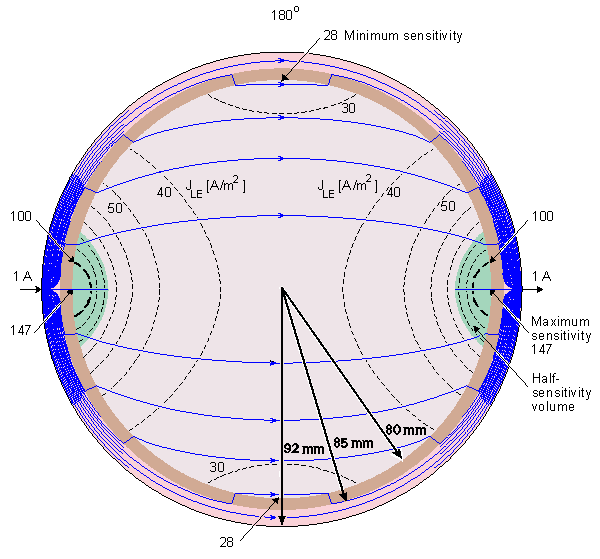
Fig. 13.4. Sensitivity distribution of EEG electrodes in the spherical head model. The figure illustrates the lead field current flow lines (thin solid lines), isosensitivity lines (dotted lines) and the half-sensitivity volumes (shaded region). The sensitivity distribution is in the direction of the flow lines, and its magnitude is proportional to the density of the flow lines. The lead pairs are designated by small arrows at the surface of the scalp and are separated by an angle of 180°, 120°, 60°, 40°, and 20° shown at the top of each figure.
13.5 THE BEHAVIOR OF THE EEG SIGNAL
From the EEG signal it is possible to differentiate alpha (α), beta (β), delta (δ), and theta (Θ) waves as well as spikes associated with epilepsy. An example of each waveform is given in Figure 13.5. The alpha waves have the frequency spectrum of 8-13 Hz and can be measured from the occipital region in an awake person when the eyes are closed. The frequency band of the beta waves is 13-30 Hz; these are detectable over the parietal and frontal lobes. The delta waves have the frequency range of 0.5-4 Hz and are detectable in infants and sleeping adults. The theta waves have the frequency range of 4-8 Hz and are obtained from children and sleeping adults..
The alpha waves have the frequency spectrum of 8-13 Hz and can be measured from the occipital region in an awake person when the eyes are closed. The frequency band of the beta waves is 13-30 Hz; these are detectable over the parietal and frontal lobes. The delta waves have the frequency range of 0.5-4 Hz and are detectable in infants and sleeping adults. The theta waves have the frequency range of 4-8 Hz and are obtained from children and sleeping adults..

- Fig. 13.5. Some examples of EEG waves.
13.6 THE BASIC PRINCIPLES OF EEG DIAGNOSIS
The EEG signal is closely related to the level of consciousness of the person. As the activity increases, the EEG shifts to higher dominating frequency and lower amplitude. When the eyes are closed, the alpha waves begin to dominate the EEG. When the person falls asleep, the dominant EEG frequency decreases. In a certain phase of sleep, rapid eye movement called (REM) sleep, the person dreams and has active movements of the eyes, which can be seen as a characteristic EEG signal. In deep sleep, the EEG has large and slow deflections called delta waves. No cerebral activity can be detected from a patient with complete cerebral death. Examples of the above-mentioned waveforms are given in Figure 13.6..
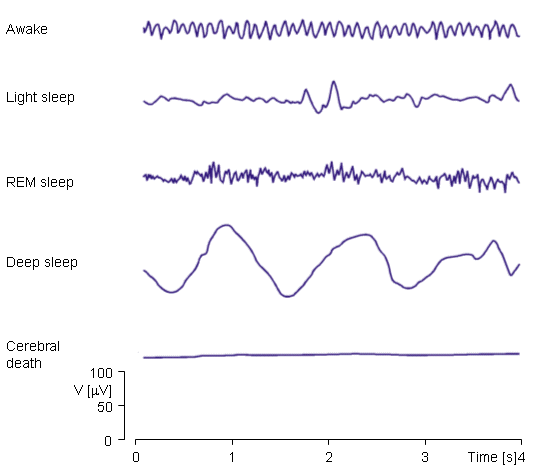
- Fig. 13.6. EEG activity is dependent on the level of consciousness.
REFERENCES
Berger H (1929): Über das Elektroenkephalogramm des Menschen. Arch. f. Psychiat. 87: 527-70.
Blumhardt LD, Barrett G, Halliday AM, Kriss A (1977): The asymmetrical visual evoked potential to pattern reversal in one half field and its significance for the analysis of visual field effects. Br. J. Ophthalmol. 61: 454-61.
Cooper R, Osselton JW, Shaw JC (1969): EEG Technology, 2nd ed., 275 pp. Butterworths, London.
Gilmore RL (1994): J. Clin. Neurophysiol RL Gilmore (ed.): American Electroencephalographic Society guidelines in electroencephalography, evoked potentials, and polysomnography, J. Clin. Neurophysiol. 11:(1, January) 147 pp.
Jasper HH (1958): Report of the Committee on Methods of Clinical Examination in Electroencephalography. Electroenceph. Clin. Neurophysiol. 10: 370-1.
Nunez PL (1981): Electric Fields of the Brain: The Neurophysics of EEG, 484 pp. Oxford University Press, New York.
Puikkonen J, Malmivuo JA (1987): Theoretical investigation of the sensitivity distribution of point EEG-electrodes on the three concentric spheres model of a human head - An application of the reciprocity theorem. Tampere Univ. Techn., Inst. Biomed. Eng., Reports 1:(5) 71.
Rush S, Driscoll DA (1969): EEG-electrode sensitivity - An application of reciprocity. IEEE Trans. Biomed. Eng. BME-16:(1) 15-22.
Sharbrough F, Chatrian G-E, Lesser RP, Lüders H, Nuwer M, Picton TW (1991): American Electroencephalographic Society Guidelines for Standard Electrode Position Nomenclature. J. Clin. Neurophysiol 8: 200-2.
Suihko V, Malmivuo JA, Eskola H (1993): Distribution of sensitivity of electric leads in an inhomogeneous spherical head model. Tampere Univ. Techn., Ragnar Granit Inst., Rep. 7:(2) .