16.1 INTRODUCTION
In the first article concerning the human electrocardiogram published in 1887, Augustus D. Waller pointed out the dipolar nature of the cardiac electric generator (Waller, 1887; see Figure 1.17). Because it is possible to describe the electric generator of the heart reasonably accurately with an equivalent dipole, called the electric heart vector (EHV), it is natural to display it in vector form. The measurement and display of the electric heart vector is called vectorcardiography (VCG), or vectorelectrocardiography (VECG) to separate it from vectormagnetocardiography (VMCG). Theoretically, an obvious way to display the behavior of the dipole is with an oscilloscope that follows the trajectory of the end point of the vector projected on to principal planes. This display is called spatial vectorcardiography. This is illustrated in Figure 16.1. The rectangular coordinate system is a natural selection. These coordinate axes may be either the body axes or the cardiac axes.
Theoretically, an obvious way to display the behavior of the dipole is with an oscilloscope that follows the trajectory of the end point of the vector projected on to principal planes. This display is called spatial vectorcardiography. This is illustrated in Figure 16.1. The rectangular coordinate system is a natural selection. These coordinate axes may be either the body axes or the cardiac axes.
 One can display the temporal information (the time scale) by modulating the intensity of the oscilloscope beam so that the trace is periodically interrupted (possibly at 2 ms intervals). By modulation the oscilloscope intensity with a triangular waveform, each 2 ms segment has a teardrop shape which indicates the direction of the trajectory.
One can display the temporal information (the time scale) by modulating the intensity of the oscilloscope beam so that the trace is periodically interrupted (possibly at 2 ms intervals). By modulation the oscilloscope intensity with a triangular waveform, each 2 ms segment has a teardrop shape which indicates the direction of the trajectory.
 The signal may also be displayed by showing the three vector components as functions of time. This display is called scalar vectorcardiography. This display is not used very often in vectorcardiography, because it provides no information that is not in the scalar display of the 12-lead ECG
The signal may also be displayed by showing the three vector components as functions of time. This display is called scalar vectorcardiography. This display is not used very often in vectorcardiography, because it provides no information that is not in the scalar display of the 12-lead ECG

Fig. 16.1. The basic principle of vectorcardiography is illustrated based on ideal uniform lead fields which are mutually orthogonal being set up by parallel electrodes on opposite sides of the torso (bipolar configuration).
 There are both uncorrected and corrected VCG lead systems. The uncorrected VCG systems do not consider the distortions caused by the boundary and internal inhomogeneities of the body. The uncorrected lead systems assume that the direction of the spatial line connecting an electrode pair yields the orientation of the corresponding lead vector. Currently it is known that this assumption is inaccurate, as is discussed later. In any event, these uncorrected lead systems are no longer in clinical use.
There are both uncorrected and corrected VCG lead systems. The uncorrected VCG systems do not consider the distortions caused by the boundary and internal inhomogeneities of the body. The uncorrected lead systems assume that the direction of the spatial line connecting an electrode pair yields the orientation of the corresponding lead vector. Currently it is known that this assumption is inaccurate, as is discussed later. In any event, these uncorrected lead systems are no longer in clinical use.
 The goal of the corrected lead system is to perform an orthonormal measurement of the electric heart vector. In an orthonormal measurement both of the following requirements are fulfilled:
The goal of the corrected lead system is to perform an orthonormal measurement of the electric heart vector. In an orthonormal measurement both of the following requirements are fulfilled:
- The three measured components of the electric heart vector are orthogonal and in the direction of the coordinate axes (i.e., the lead vectors are parallel to the coordinate axes, which are usually the body axes). Furthermore, each lead field is uniform throughout the heart.
- Each of the three components of the electric heart vector are detected with the same sensitivity; that is, the measurements are normalized.
 In the corrected vectorcardiographic lead systems the accuracy of the orthonormal measurement is limited by the applied theoretical method. The theoretical methods for analyzing volume sources and volume conductors were discussed earlier in Chapter 9. Each of them has allowed for a VCG system to be orthonormal within the limits of the performed correction. These lead systems are discussed in detail later in this chapter.
In the corrected vectorcardiographic lead systems the accuracy of the orthonormal measurement is limited by the applied theoretical method. The theoretical methods for analyzing volume sources and volume conductors were discussed earlier in Chapter 9. Each of them has allowed for a VCG system to be orthonormal within the limits of the performed correction. These lead systems are discussed in detail later in this chapter.
 What is the clinical importance of vectorcardiography? The answer is that the information content of the VCG is the same, roughly, as that of the leads V2, V6 and aVF in the 12-lead system, though it is obtained in corrected (orthonormal) form. It is true that the information content in the VCG signal is not greater than in the scalar ECG. However, the display system provides an opportunity to analyze the progress of the activation front in a different way, especially its initial and terminal parts. It is also much easier to observe the direction of the heart vector from the VCG loops. Additionally, the area of the loops, which is not easy to observe from a scalar display, may have clinical importance.
What is the clinical importance of vectorcardiography? The answer is that the information content of the VCG is the same, roughly, as that of the leads V2, V6 and aVF in the 12-lead system, though it is obtained in corrected (orthonormal) form. It is true that the information content in the VCG signal is not greater than in the scalar ECG. However, the display system provides an opportunity to analyze the progress of the activation front in a different way, especially its initial and terminal parts. It is also much easier to observe the direction of the heart vector from the VCG loops. Additionally, the area of the loops, which is not easy to observe from a scalar display, may have clinical importance.
 In this chapter we introduce representative examples of the large number of uncorrected and corrected vectorcardiographic lead systems.
In this chapter we introduce representative examples of the large number of uncorrected and corrected vectorcardiographic lead systems.
16.2 UNCORRECTED VECTORCARDIOGRAPHIC LEAD SYSTEMS
PRECONDITIONS:SOURCE: Dipole in a fixed location
CONDUCTOR: Infinite, homogeneous volume conductor or homogeneous sphere with the dipole in its center (the trivial solution)
16.2.1 Monocardiogram by Mann
Though Waller was the first to record a set of three nearly orthogonal leads, namely mouth-to-left arm, mouth-to-left leg and back-to-front, he did not display them in vector form. It was Hubert Mann who in 1920 first suggested the concept of vectorcardiography by publishing a monocardiogram, which he constructed manually from the limb leads of Einthoven, as shown in Figure 1.18 (Mann, 1920). The monocardiogram of Mann is the projection of the vector loop in the frontal plane, assuming the validity of the Einthoven triangle lead vectors which it uses to interpret the limb lead voltages. Therefore, it is only two-dimensional, and it excludes the back-to-front information from the sagittal and transverse planes. (Note that Mann placed the signals of the leads I, II, and III to the lead vectors in opposite polarity. Therefore, the vector loop is oriented upward and right, though it actually should be oriented downward and left.) Mann also constructed a special mirror galvanometer that allowed the display of the monocardiogram directly from ECG signals; see Figure 16.2 (Mann, 1938a). This mirror galvanometer included three coils arranged in one plane and located symmetrically in 120° intervals around a mirror. They were situated in a constant magnetic field produced by a large coil. When the three coils were driven by amplified ECG signals from leads I, II, and III, the net torque of this coil assembly produced a deflection of the mirror, and a ray of light it reflected, proportional to the electric heart vector. Thus Mann's mirror galvanometer was actually an analog computer calculating the monocardiogram from the three limb leads. The work of Mann was largely ignored for more than 15 years. It had to await the invention of the cathode ray tube in the 1930s when it was possible to apply electronic devices to display the projections of the vector loop (Mann, 1931, 1938b).
Mann also constructed a special mirror galvanometer that allowed the display of the monocardiogram directly from ECG signals; see Figure 16.2 (Mann, 1938a). This mirror galvanometer included three coils arranged in one plane and located symmetrically in 120° intervals around a mirror. They were situated in a constant magnetic field produced by a large coil. When the three coils were driven by amplified ECG signals from leads I, II, and III, the net torque of this coil assembly produced a deflection of the mirror, and a ray of light it reflected, proportional to the electric heart vector. Thus Mann's mirror galvanometer was actually an analog computer calculating the monocardiogram from the three limb leads. The work of Mann was largely ignored for more than 15 years. It had to await the invention of the cathode ray tube in the 1930s when it was possible to apply electronic devices to display the projections of the vector loop (Mann, 1931, 1938b).
 An interesting invention in the vectorcardiography instrumentation was the cathode ray tube of W. Hollman and H. F. Hollman (1939). They used three pairs of deflection plates arranged at 120° angles with respect to one another corresponding to the directions of the three edges of the Einthoven triangle (see Figure 16.3). When these deflection plates were driven with amplified leads I, II, and III, the tube produced on the screen a monocardiogram similar to Mann's mirror galvanometer on a film.
An interesting invention in the vectorcardiography instrumentation was the cathode ray tube of W. Hollman and H. F. Hollman (1939). They used three pairs of deflection plates arranged at 120° angles with respect to one another corresponding to the directions of the three edges of the Einthoven triangle (see Figure 16.3). When these deflection plates were driven with amplified leads I, II, and III, the tube produced on the screen a monocardiogram similar to Mann's mirror galvanometer on a film.
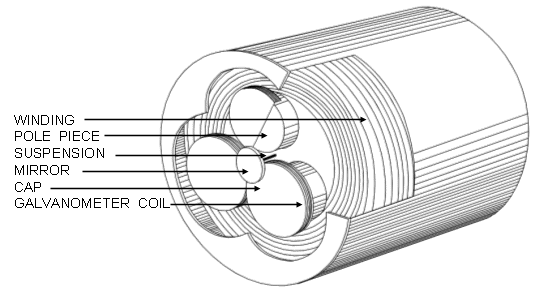
Fig. 16.2 The mirror vectorcardiograph constructed by Hubert Mann was the first instrument to produce a vectorcardiogram. It has three coils symmetrically placed at 120° intervals around a mirror. Thus it produces a vectorcardiogram in the frontal plane from the three limb leads of Einthoven. (Mann, 1938a).

- Fig. 16.3 The cathode ray tube of W. Hollman and H. F. Hollman has three pairs of deflection plates oriented in the directions of the edges of the Einthoven triangle. Thus it produces the vectorcardiogram in the frontal plane from the Einthoven limb leads. (Hollman and Hollman, 1937)
16.2.2 Lead Systems Based on Rectangular Body Axes
Most of the uncorrected and corrected vectorcardiographic lead systems are based on the rectangular body axes. From the large number of such uncorrected VCG lead systems, we briefly mention the following ones in this section. After inventing the central terminal in 1932, Frank Norman Wilson logically progressed to the development of a lead system for vectorcardiography. Wilson and his co-workers published a lead system that added to the Einthoven limb leads an electrode located on the back (about 2.5 cm to the left from the seventh dorsal vertebra) (Wilson and Johnston, 1938, Wilson, Johnston, and Kossmann 1947). The four electrodes formed the corners of a tetrahedron, as shown in Figure 16.4, and consequently permitted the back-to-front component of the heart vector to be recognized. The three components of the electric heart vector were measured as follows (expressed in the consistent coordinate system described in the Appendix): The x-component was measured between the electrode on the back and the Wilson central terminal. The y-component was lead I, and the z-component was lead -VF. This lead system, called the Wilson tetrahedron, was the first to display the three components of the electric heart vector.
After inventing the central terminal in 1932, Frank Norman Wilson logically progressed to the development of a lead system for vectorcardiography. Wilson and his co-workers published a lead system that added to the Einthoven limb leads an electrode located on the back (about 2.5 cm to the left from the seventh dorsal vertebra) (Wilson and Johnston, 1938, Wilson, Johnston, and Kossmann 1947). The four electrodes formed the corners of a tetrahedron, as shown in Figure 16.4, and consequently permitted the back-to-front component of the heart vector to be recognized. The three components of the electric heart vector were measured as follows (expressed in the consistent coordinate system described in the Appendix): The x-component was measured between the electrode on the back and the Wilson central terminal. The y-component was lead I, and the z-component was lead -VF. This lead system, called the Wilson tetrahedron, was the first to display the three components of the electric heart vector.
 The lead system of F. Schellong, S. Heller, and G. Schwingel (1937) is two-dimensional, presenting the vector loop only in the frontal plane. The other lead systems - those of Noboru Kimura (1939), Pierre Duchosal and R. Sulzer (1949), A. Grishman and L. Scherlis (1952), and William Milnor, S. Talbot, and E. Newman (1953) - also include the third dimension. These lead systems are illustrated in Figure 16.5. Because of their geometry, the lead system of Grishman and Scherlis was called the "Grishman cube" and the lead system of Duchosal and Schultzer the "double cube.".
The lead system of F. Schellong, S. Heller, and G. Schwingel (1937) is two-dimensional, presenting the vector loop only in the frontal plane. The other lead systems - those of Noboru Kimura (1939), Pierre Duchosal and R. Sulzer (1949), A. Grishman and L. Scherlis (1952), and William Milnor, S. Talbot, and E. Newman (1953) - also include the third dimension. These lead systems are illustrated in Figure 16.5. Because of their geometry, the lead system of Grishman and Scherlis was called the "Grishman cube" and the lead system of Duchosal and Schultzer the "double cube.".

- Fig. 16.4 The electrodes of the Wilson tetrahedron lead system.

- Fig. 16.5 Uncorrected VCG lead systems based on rectangular body axes.
16.2.3 Akulinichev VCG Lead Systems
Ivan T. Akulinichev developed two uncorrected VCG-lead systems, one applying five display planes (Akulinichev, 1956) and another one applying three planes (Akulinichev, 1960). In the five-plane system, which he proposed in 1951, the electrodes are located in the corners of a pyramid so that four electrodes are on the anterior side of the thorax and the fifth is on the back, left from the spine on the level of the inferior angle of the scapula. In the five-plane Akulinichev system projection I is the frontal plane. The other four projections have different posterior views (Figure 16.6A). Projection II examines the left ventricle in a left-superior-posterior view. Projections III and IV are right-inferior-posterior and left-inferior-posterior views, respectively. Projection V examines the atria in a right-superior-posterior view. Note that in the frontal plane the measurement between the electrodes 1 and 3 is oriented approximately along the main axis of the heart. The five projections of the electric heart vector recorded with the Akulinichev system are shown in Figure 16.6B. Because two projections are necessary and sufficient for displaying a spatial vector loop, the five-plane Akulinichev system includes more redundant information than systems with three projections.
In the five-plane Akulinichev system projection I is the frontal plane. The other four projections have different posterior views (Figure 16.6A). Projection II examines the left ventricle in a left-superior-posterior view. Projections III and IV are right-inferior-posterior and left-inferior-posterior views, respectively. Projection V examines the atria in a right-superior-posterior view. Note that in the frontal plane the measurement between the electrodes 1 and 3 is oriented approximately along the main axis of the heart. The five projections of the electric heart vector recorded with the Akulinichev system are shown in Figure 16.6B. Because two projections are necessary and sufficient for displaying a spatial vector loop, the five-plane Akulinichev system includes more redundant information than systems with three projections.
 From the five-plane VCG system, Akulinichev developed later the three-plane VCG system (Akulinichev, 1960; Pawlov, 1966; Wenger, 1969). A characteristic of this lead system is that the main coordinate axes of the system are oriented along the main axes of the heart. The exact locations of the electrodes are (see Figure 16.7) as follows: 1 = right arm, 2 = left arm, 4 = V2, 5 = V5, 6 = on the right side of xiphoid, 7 = V9 (on the posterior surface of the thorax, at the left side of the spine on the level of V4 and V5). The three projections are formed as follows: projection I = electrodes 1, 2, 5, and 6 (i.e., the frontal plane); projection II = electrodes 1, 7, 5, and 4 (i.e., parallel to the longitudinal axis of the heart); projection III = electrodes 6, 7, 2, and 4 (i.e., the cross-sectional plane of the heart).
From the five-plane VCG system, Akulinichev developed later the three-plane VCG system (Akulinichev, 1960; Pawlov, 1966; Wenger, 1969). A characteristic of this lead system is that the main coordinate axes of the system are oriented along the main axes of the heart. The exact locations of the electrodes are (see Figure 16.7) as follows: 1 = right arm, 2 = left arm, 4 = V2, 5 = V5, 6 = on the right side of xiphoid, 7 = V9 (on the posterior surface of the thorax, at the left side of the spine on the level of V4 and V5). The three projections are formed as follows: projection I = electrodes 1, 2, 5, and 6 (i.e., the frontal plane); projection II = electrodes 1, 7, 5, and 4 (i.e., parallel to the longitudinal axis of the heart); projection III = electrodes 6, 7, 2, and 4 (i.e., the cross-sectional plane of the heart).
 The Akulinichev lead systems have been applied in the (former) Soviet Union and Bulgaria since the 1960s and they are virtually the only clinical vectorcardiographic systems used there to date.
The Akulinichev lead systems have been applied in the (former) Soviet Union and Bulgaria since the 1960s and they are virtually the only clinical vectorcardiographic systems used there to date.
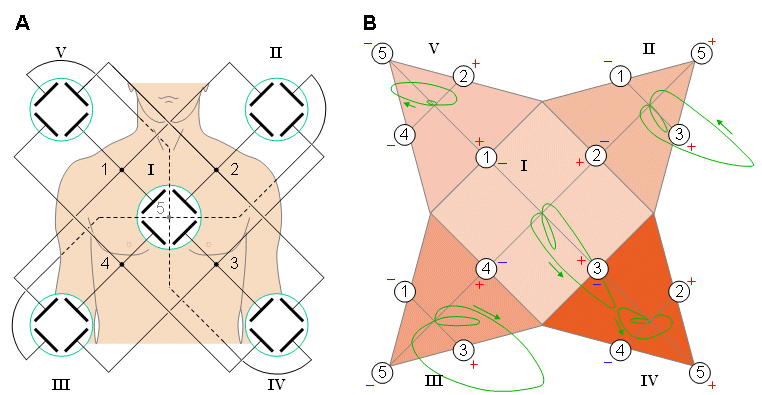
- Fig. 16.6 Five-plane Akulinichev VCG system.
 (A) Location of the electrodes on the thorax and their five connections to the oscilloscope.
(A) Location of the electrodes on the thorax and their five connections to the oscilloscope.
 (B) The five projections of the electric heart vector.
(B) The five projections of the electric heart vector.
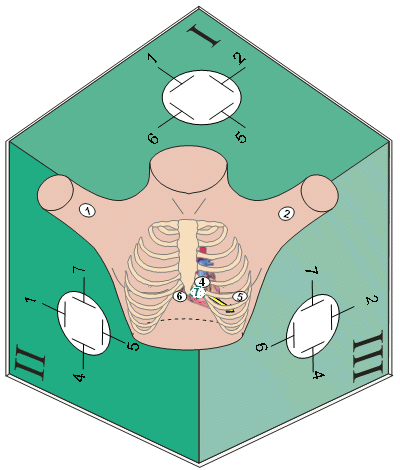
- Fig. 16.7 Three-plane Akulinichev VCG system.
16.3 CORRECTED VECTORCARDIOGRAPHIC LEAD SYSTEMS
16.3.1 Frank Lead System
PRECONDITIONS:SOURCE: Dipole in a fixed location
CONDUCTOR: Finite, homogeneous
In 1956 Ernest Frank (Frank, 1956) published a vectorcardiographic lead system that was based on his previously published data of image surface (Frank, 1954). Because the image surface was measured for a finite, homogeneous thorax model, the volume conductor model for the Frank VCG-lead system was also the same. In the following, we first discuss the design principles of the Frank lead system. Then we discuss the construction of each orthogonal component of the measurement system. Though we refer here to the original publication of Frank, we use the consistent coordinate system described in the Appendix.
Electrode Location Requirements
To measure the three dipole components, at least four electrodes (one being a reference) are needed. Frank decided to increase the number of electrodes to seven, in order to decrease the error due to interindividual variation in the heart location and body shape. It is important that the electrode location can be easily found to increase the reproducibility of the measurement. The reproducibility of the limb electrodes is very good. However, the arm electrodes have the problem that the lead fields change remarkably if the patient touches the sides with the arms, because the electric current flows through the wet skin directly to the thorax. This problem has a special importance to the left arm, since the heart is closer. Figure 16.8A.
It is important that the electrode location can be easily found to increase the reproducibility of the measurement. The reproducibility of the limb electrodes is very good. However, the arm electrodes have the problem that the lead fields change remarkably if the patient touches the sides with the arms, because the electric current flows through the wet skin directly to the thorax. This problem has a special importance to the left arm, since the heart is closer. Figure 16.8A.
Determination of the Electrode Location
Based on the above requirements Frank devised a lead system, now bearing his name, which yields corrected orthogonal leads. Electrode numbers and positions were chosen very deliberately, and were based upon his image surface model (Figure 11.14). He selected level 6 for electrode placement, because the lead vectors are largest on this level. Specifically, he chose the points designated A, E, I, and M on the left, front, right, and back, respectively. He also chose point C between points A and E because it is close to the heart. In addition, a point on the neck and one on the left foot were included.Right-to-Left Component (y-Component)
We begin with the right-to-left component (y-component) because its construction is the simplest and easy to understand. The lead vector in this direction is determined by applying previously mentioned methods to Figure 16.8. This figure shows the anatomic view of level 6 as well as its image surface as measured by Frank. The image space locations of electrodes A, C, and I are also shown since these were chosen to sense the y-component of the heart vector. The basic principle in the design of the y-component of the lead system is to synthesize in image space, with the available electrode points, a lead vector that is oriented in the y-direction. This is the only requirement that must be fulfilled for the lead to record the y-component.
The basic principle in the design of the y-component of the lead system is to synthesize in image space, with the available electrode points, a lead vector that is oriented in the y-direction. This is the only requirement that must be fulfilled for the lead to record the y-component.
 Additionally, it is advantageous to select from among all those lead vectors that are in the y-direction the one that is the largest. This ensures a signal-to-noise ratio that is as high as possible.
Additionally, it is advantageous to select from among all those lead vectors that are in the y-direction the one that is the largest. This ensures a signal-to-noise ratio that is as high as possible.
 If we designate image space point I' as one end point of the selected lead vector parallel to the y-axis, its other end point is found on line A'-C', and is labeled point a'. Point a' divides A'-C' in the proportion 1:3.59. By connecting two resistors having values in this ratio between the points A and C in real space, the point a is realized at their intersection.
If we designate image space point I' as one end point of the selected lead vector parallel to the y-axis, its other end point is found on line A'-C', and is labeled point a'. Point a' divides A'-C' in the proportion 1:3.59. By connecting two resistors having values in this ratio between the points A and C in real space, the point a is realized at their intersection.
 From a practical point of view it is important that the impedance the amplifier sees in each lead be equal. A good balance ensures cancellation of common mode noise signals. If we designate this impedance as R, we have to add such a resistor to the lead in electrode I and to multiply the parallel resistors of electrodes A and C by the factor 1.28. This yields resistor values 1.28R and 4.59R, respectively. (Note that now the parallel resistance of these two resistors is R.) From a measurement in image space we determine the length of the lead vector y to be 174 relative units..
From a practical point of view it is important that the impedance the amplifier sees in each lead be equal. A good balance ensures cancellation of common mode noise signals. If we designate this impedance as R, we have to add such a resistor to the lead in electrode I and to multiply the parallel resistors of electrodes A and C by the factor 1.28. This yields resistor values 1.28R and 4.59R, respectively. (Note that now the parallel resistance of these two resistors is R.) From a measurement in image space we determine the length of the lead vector y to be 174 relative units..
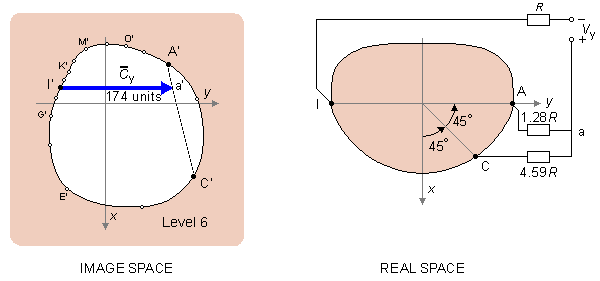
- Fig. 16.8 Determination of the right-to-left component (y-component) in the Frank lead system. The image space shown on the left corresponds to the actual transverse plane on the right.
Foot-to-Head Component (z-Component)
From the image space in Figure 16.9, we can verify that if we select for one end of the image vector the point H' on level 1 (i.e., on the neck), there exists a point k' on line F'-M' such that K'-H' forms a lead vector parallel to the z-axis. The point k' divides the axis in proportion 1:1.9. Again the lead is balanced by placing a resistor R in series with electrode H and by multiplying the resistors in electrodes F and M by a factor 1.53 which leads to values of 1.53R and 2.90R, respectively. The length of the lead vector z is 136 units.Back-to-Front Component (x-Component)
In the design of the x-component Frank wanted, in addition to the previous requirements, to select such a weighing for the electrodes that the lead vector variation throughout the heart would be as uniform as possible. Consequently, Frank used all the five electrodes on level 6. The transverse plane projection of the image surface is shown again in Figure 16.10, and electrodes A, C, E, I, and M are described in both real and image space. Frank drew the lines A'-M', E'-C' and g'-I' in the image space, from which the point g' was located on the line E'-C'. Between the lines A'-M' and g'-I' he drew a line segment f'-h' parallel to the x-axis. This is the lead vector corresponding to the x-lead and fully meets the requirements discussed above.
Frank drew the lines A'-M', E'-C' and g'-I' in the image space, from which the point g' was located on the line E'-C'. Between the lines A'-M' and g'-I' he drew a line segment f'-h' parallel to the x-axis. This is the lead vector corresponding to the x-lead and fully meets the requirements discussed above.
 The physical realization of the lead that corresponds to the chosen lead vector is found as follows: From the image space, it is possible to ascertain that the point f' divides the segment of line A'-M' in the proportion 5.56:1. Multiplying these with 1.18, we obtain values 6.56:1.18 having a parallel resistance value of 1. By connecting two resistors of similar proportions in series, between the electrodes A and M, we find that their point of connection in real space is f.
The physical realization of the lead that corresponds to the chosen lead vector is found as follows: From the image space, it is possible to ascertain that the point f' divides the segment of line A'-M' in the proportion 5.56:1. Multiplying these with 1.18, we obtain values 6.56:1.18 having a parallel resistance value of 1. By connecting two resistors of similar proportions in series, between the electrodes A and M, we find that their point of connection in real space is f.
 Similarly the point g' divides the image space segment of line C'-E' in the proportion 1.61:1. The parallel value of these is 0.62. The point h' divides the segment of line g'-I' in the proportion 1:2.29. If we multiply this by 0.62, we get 0.62:1.41. Now we have the relative resistor values 1.61, 1, and 1.41 to electrodes C, E, and I, respectively. To adjust their parallel resistances to be equal to 1, we multiply each by 2.32 and we obtain 3.74R, 2.32R, and 3.72R. Now we have synthesized the lead vector
Similarly the point g' divides the image space segment of line C'-E' in the proportion 1.61:1. The parallel value of these is 0.62. The point h' divides the segment of line g'-I' in the proportion 1:2.29. If we multiply this by 0.62, we get 0.62:1.41. Now we have the relative resistor values 1.61, 1, and 1.41 to electrodes C, E, and I, respectively. To adjust their parallel resistances to be equal to 1, we multiply each by 2.32 and we obtain 3.74R, 2.32R, and 3.72R. Now we have synthesized the lead vector 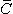 x ; relative to the assumed image space scale, it has a magnitude of 156 units..
x ; relative to the assumed image space scale, it has a magnitude of 156 units..
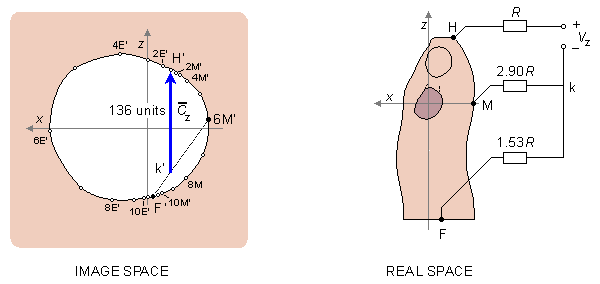
Fig. 16.9 Determination of the foot-to-head component (z-component) in the Frank lead system. The image space shown on the left corresponds to the actual sagittal plane on the right.
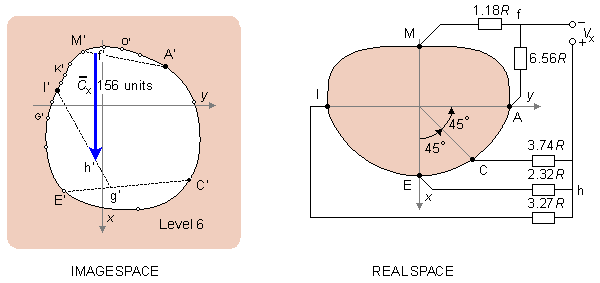
Fig. 16.10 Determination of the back-to-front component (x-component) in the Frank lead system. The image space shown on the left corresponds to the actual transverse plane on the right.
Frank Lead Matrix
We have now determined all three lead vectors that form an orthogonal lead system. This system must still be normalized. Therefore, resistors 13.3R and 7.15R are connected between the leads of the x- and y-components to attenuate these signals to the same level as the z-lead signal. Now the Frank lead system is orthonormal. It should be noted once again that the resistance of the resistor network connected to each lead pair is unity. This choice results in a balanced load and increases the common mode rejection ratio of the system. The absolute value of the lead matrix resistances may be determined once the value of R is specified. For this factor Frank recommended that it should be at least 25kΩ, and preferably 100 kΩ. Nowadays the lead signals are usually detected with a high-impedance preamplifier, and the lead matrix function is performed by operational amplifiers or digitally thereafter. Figure 16.11 illustrates the complete Frank lead matrix.
It should be noted once again that the resistance of the resistor network connected to each lead pair is unity. This choice results in a balanced load and increases the common mode rejection ratio of the system. The absolute value of the lead matrix resistances may be determined once the value of R is specified. For this factor Frank recommended that it should be at least 25kΩ, and preferably 100 kΩ. Nowadays the lead signals are usually detected with a high-impedance preamplifier, and the lead matrix function is performed by operational amplifiers or digitally thereafter. Figure 16.11 illustrates the complete Frank lead matrix.
 It is worth mentioning that the Frank system is presently the most common of all clinical VCG systems throughout the world. (However, VCG's represent less than 5% of the electrocardiograms.).
It is worth mentioning that the Frank system is presently the most common of all clinical VCG systems throughout the world. (However, VCG's represent less than 5% of the electrocardiograms.).
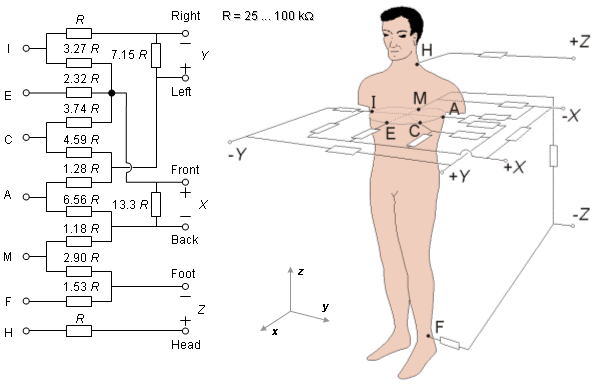
Fig. 16.11 The lead matrix of the Frank VCG-system. The electrodes are marked I, E, C, A, M, F, and H, and their anatomical positions are shown. The resistor matrix results in the establishment of normalized x-, y-, and z-component lead vectors, as described in the text.
16.3.2 McFee-Parungao Lead System
PRECONDITIONS:SOURCE: Dipole moment of a volume source
CONDUCTOR: Finite, homogeneous
McFee and Parungao (1961) published a simple VCG lead system called the axial system, based on a lead field theoretic approach. In addition, the heart was modeled with a volume source and the thorax was assumed to be homogeneous.
 The three uniform lead fields were designed according to the principle discussed in Section 11.6.10. To detect the three orthogonal components of the electric heart vector, three pairs of (single or multiple) electrodes must be used on each coordinate axis, one on either side of the heart. McFee and Parungao recognized that the closer to the heart the electrodes are placed the more electrodes must be used to achieve a homogeneous lead field within the heart's area.
The three uniform lead fields were designed according to the principle discussed in Section 11.6.10. To detect the three orthogonal components of the electric heart vector, three pairs of (single or multiple) electrodes must be used on each coordinate axis, one on either side of the heart. McFee and Parungao recognized that the closer to the heart the electrodes are placed the more electrodes must be used to achieve a homogeneous lead field within the heart's area.
Back-to-Front Component (x-Component)
McFee and Parungao felt that three anterior electrodes should be assigned to the measurement of the back-to-front component of the VCG. This would generate a lead field with sufficient homogeneity even though the heart is close to the anterior wall of the thorax. They followed the method of synthesizing ideal lead fields as discussed in Section 11.5.8. By connecting 100 kΩ resistances to each electrode, the net lead impedance is 33 kΩ. The accurate location of the chest electrodes is found as follows: The electrodes form an equilateral triangle so oriented that its base is nearest to the subject's feet. The electrodes are at a distance of 6 cm from the center of the triangle. The center of the triangle is in the fifth intercostal space, 2 cm to the left of the sternal margin. This position should ensure that the chest electrodes are located directly above the center of gravity of the ventricles. (This is illustrated in Figure 16.12.)
The accurate location of the chest electrodes is found as follows: The electrodes form an equilateral triangle so oriented that its base is nearest to the subject's feet. The electrodes are at a distance of 6 cm from the center of the triangle. The center of the triangle is in the fifth intercostal space, 2 cm to the left of the sternal margin. This position should ensure that the chest electrodes are located directly above the center of gravity of the ventricles. (This is illustrated in Figure 16.12.)
 Because the posterior wall of the thorax is more distant from the heart, only one electrode is needed there. The back electrode lies directly behind the center of the chest triangle. McFee and Parungao did not balance the lead system against common mode noise. The authors suggest that if a 33 kΩ resistor were connected to the back electrode, the balancing requirement, discussed earlier, would be fulfilled.
Because the posterior wall of the thorax is more distant from the heart, only one electrode is needed there. The back electrode lies directly behind the center of the chest triangle. McFee and Parungao did not balance the lead system against common mode noise. The authors suggest that if a 33 kΩ resistor were connected to the back electrode, the balancing requirement, discussed earlier, would be fulfilled.
Right-to-Left Component (y-component)
For the y-component the same procedure as described above was followed. McFee and Parungao placed two electrodes with 66 kΩ resistances on the left side and one electrode on the right side of the thorax. The right electrode is located on the same level as the center of the electrode triangle on the chest. It is placed on the right side, one third of the way from the chest to the back. The electrodes on the left side are also located one third of the way toward the back at longitudinal levels 5.5 cm over and below the level of the center of the chest triangle. The electrode spacing is therefore 11 cm. These produce reasonably uniform right-to-left lead fields in the region of the heart. McFee and Parungao did not balance the y-lead either. The authors suggest that adding a 33 kΩ resistor to the electrode on the right balances the lead against common mode noise.
McFee and Parungao did not balance the y-lead either. The authors suggest that adding a 33 kΩ resistor to the electrode on the right balances the lead against common mode noise.
Foot-to-Head Component (z-Component)
The electrodes designed to measure the z-component of the VCG are so distant from the heart that McFee and Parungao used only one electrode on the neck and one on the left foot. These electrodes may be equipped with a 33 kΩ resistor for the whole lead system to be balanced. The complete McFee-Parungao VCG lead system is shown in Figure 16.12.
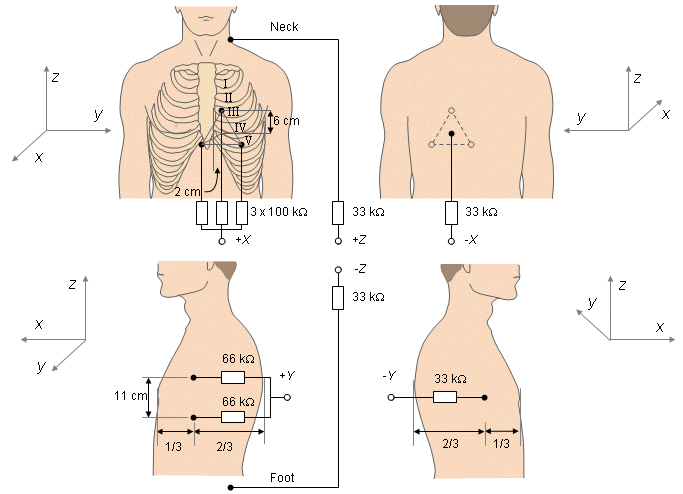
- Fig. 16.12 McFee-Parungao VCG lead system.
16.3.3 SVEC III Lead System
PRECONDITIONS:SOURCE: Dipole moment of a volume source
CONDUCTOR: Finite, homogeneous
Otto H. Schmitt and Ernst Simonson developed many versions of vectorcardiographic lead systems, calling them stereovectorelectrocardiography (SVEC). The third version, SVEC III, was published in 1955 (Schmitt and Simonson, 1955). It requires a total of 14 electrodes and creates a lead field in the thorax which is very symmetric in relation to the sagittal plane. The lead system is described in Figure 16.13.
 In the SVEC III lead system, the electrodes are located on the thorax in the following way: The torso is divided angularly into 30° symmetric sectors about a central vertical axis so that, starting with 1 at the front, Arabic numerals up to 12 divide the torso vertically. Roman numerals refer to interspaces at the sternum and are carried around horizontally on a flat panel so that a grid is established on which a location such as V 7 would mean a location at the vertical level of the fifth interspace and at the middle of the back.
In the SVEC III lead system, the electrodes are located on the thorax in the following way: The torso is divided angularly into 30° symmetric sectors about a central vertical axis so that, starting with 1 at the front, Arabic numerals up to 12 divide the torso vertically. Roman numerals refer to interspaces at the sternum and are carried around horizontally on a flat panel so that a grid is established on which a location such as V 7 would mean a location at the vertical level of the fifth interspace and at the middle of the back.
Back-to-Front Component (x-Component)
The back-to-front component, the x-component, is formed from four electrodes on the back and four electrodes on the chest. The back electrodes are located at the grid points III 6, III 8, VI 6, and VI 8. Each of these electrodes is connected with a 100 kΩ resistor to the common back terminal (-X). The chest electrodes are located at grid points III 12, III 2, VI 2, and VI 12. A 70 kΩ resistor is connected from the first one (III 12), and 100 kΩ resistors are connected from the others to the common chest terminal (+X).Right-to-Left Component (y-Component)
The right terminal (-Y) is obtained by connecting 100 kΩ resistors to the right arm and to the grid point V 11. The left terminal (+Y) is formed similarly by connecting 100 k resistors to the left arm and to the grid point V 3. To normalize the lead, the gain is adjusted to the 75% level.Foot-to-Head Component (z-Component)
The z-component is obtained simply by placing electrodes to the left foot and to the head. Again, to normalize the lead, the gain is adjusted to the 71% level.
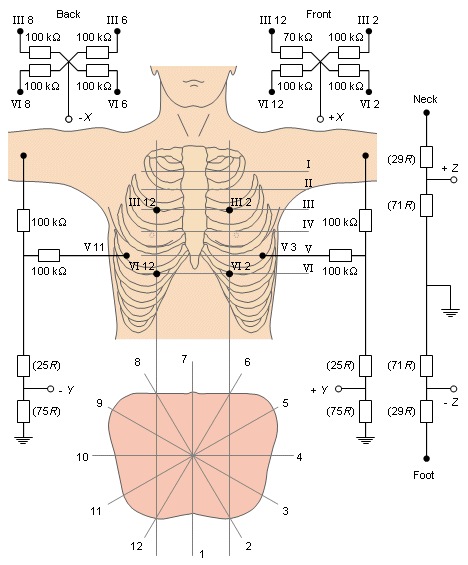
- Fig. 16.13 SVEC III VCG lead system.
16.3.4 Fischmann-Barber-Weiss Lead System
PRECONDITIONS:SOURCE: Dipole moment of a volume source with moving (optimal) location
CONDUCTOR: Finite, homogeneous
E. J. Fischmann, M. R. Barber, and G. H. Weiss (1971) constructed a VCG lead system that measures the equivalent electric dipole according to the Gabor-Nelson theorem.
 Their equipment consisted of a matrix of 7 × 8 electrodes on the back of the patient and 11 × 12 on the chest. The latter were fixed on rods that could move along their axes. Similar electrode matrices with 7 × 7 electrodes were also placed on the sides of the patient. When the moving-rod electrodes are pressed against the surface of the thorax, their movement gives information about the thorax shape. This information is needed in the solution of the Gabor-Nelson equation.
Their equipment consisted of a matrix of 7 × 8 electrodes on the back of the patient and 11 × 12 on the chest. The latter were fixed on rods that could move along their axes. Similar electrode matrices with 7 × 7 electrodes were also placed on the sides of the patient. When the moving-rod electrodes are pressed against the surface of the thorax, their movement gives information about the thorax shape. This information is needed in the solution of the Gabor-Nelson equation.
 This lead system was not intended for clinical use but rather for the demonstration of the Gabor-Nelson theory in the measurement of the vectorcardiogram.
This lead system was not intended for clinical use but rather for the demonstration of the Gabor-Nelson theory in the measurement of the vectorcardiogram.
16.3.5 Nelson Lead System
PRECONDITIONS:SOURCE: Dipole moment of a volume source with moving (optimal) location
CONDUCTOR: Finite, homogeneous
In 1971 Clifford V. Nelson and his collaborators published a lead system suitable for clinical use based on the Gabor-Nelson theorem (Nelson et al., 1971). The lead system includes electrodes placed on three levels of the thorax with eight on each level, one electrode on the head, and one on the left leg. The electrode rows are designated A, B, and C, as shown in Figure 16.14. The levels are determined by measuring the distance H' between the suprasternal notch and umbilicus. This distance is divided by 8, and the rows are placed at 1/8 H', 4/8 H', and 7/8 H' from either notch or umbilicus.
 As shown in Figure 16.14, electrodes 1 and 5 are placed at center-back and midsternal line, respectively. Electrodes 2, 3, and 4 are equally spaced on the right side, and electrodes 6, 7, and 8 are equally spaced on the left side. If the arms intervene on level C, electrodes 3 and 7 are placed on the right arm and left arm, respectively. The angle θ is the angle between the surface of the thorax and the frontal plane.
As shown in Figure 16.14, electrodes 1 and 5 are placed at center-back and midsternal line, respectively. Electrodes 2, 3, and 4 are equally spaced on the right side, and electrodes 6, 7, and 8 are equally spaced on the left side. If the arms intervene on level C, electrodes 3 and 7 are placed on the right arm and left arm, respectively. The angle θ is the angle between the surface of the thorax and the frontal plane.
 Resistors of 500 kΩ (R) are connected to the electrodes on rows A, B, and C (see Figure 16.15). From these resistors, on each three levels four (Rx and Ry) are variable and are adjusted according to the shape of the thorax of the patient to obey the Gabor-Nelson theory. The adjustment is made so that
Resistors of 500 kΩ (R) are connected to the electrodes on rows A, B, and C (see Figure 16.15). From these resistors, on each three levels four (Rx and Ry) are variable and are adjusted according to the shape of the thorax of the patient to obey the Gabor-Nelson theory. The adjustment is made so that
 Rx /R = sin θ Rx /R = sin θ | (16.1) |
 Ry /R = cos θ Ry /R = cos θ |
where θ = the angle between the surface normal and the sagittal plane
 Nelson and co-workers claim that on the basis of their measurements this VCG lead system is much more accurate than the McFee or Frank lead systems. Furthermore, this system should be very insensitive to electrode misplacement.
Nelson and co-workers claim that on the basis of their measurements this VCG lead system is much more accurate than the McFee or Frank lead systems. Furthermore, this system should be very insensitive to electrode misplacement.
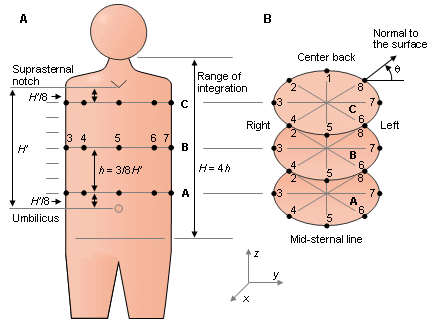
- Fig. 16.14 The electrode locations in the Nelson lead system.
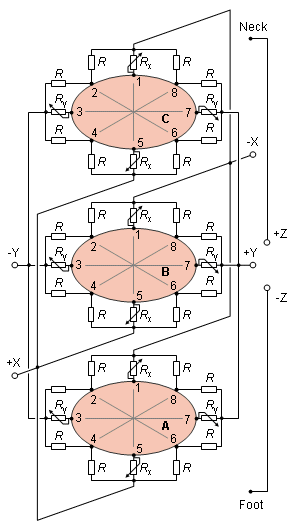
- Fig. 16.15 Electrode matrix in the Nelson VCG lead system.
16.4 DISCUSSION ON VECTORCARDIOGRAPHIC LEADS
16.4.1 The Interchangeability of Vectorcardiographic Systems
The purpose of the vectorcardiographic systems is to detect the equivalent dipole of the heart. If various systems make this measurement accurately, the measurement results should be identical. This is, however, not the case. In practice, each vectorcardiographic system gives a little different measurement result. There have been attempts to develop transformation coefficients from one system to another in order to make the various systems commensurable. If the various systems are orthogonal, these transformations should, in principle, also be orthogonal.
There have been attempts to develop transformation coefficients from one system to another in order to make the various systems commensurable. If the various systems are orthogonal, these transformations should, in principle, also be orthogonal.
 Horan, Flowers, and Brody (1965) made a careful study on the transformation coefficients between Frank, McFee-Parungao (axial-), and SVEC III lead systems for 35 normal young men. In this study it was found that the transformations between these lead systems were not orthogonal, indicating that at least two of the vectorcardiographic systems are not truly orthogonal. They also came to the conclusion that the practical interchangeability of quantitative information obtained from one lead system into that obtained by another is seriously limited because of the wide range of biologic variation in transformation characteristics.
Horan, Flowers, and Brody (1965) made a careful study on the transformation coefficients between Frank, McFee-Parungao (axial-), and SVEC III lead systems for 35 normal young men. In this study it was found that the transformations between these lead systems were not orthogonal, indicating that at least two of the vectorcardiographic systems are not truly orthogonal. They also came to the conclusion that the practical interchangeability of quantitative information obtained from one lead system into that obtained by another is seriously limited because of the wide range of biologic variation in transformation characteristics.
16.4.2 Properties of Various Vectorcardiographic Lead Systems
The previously discussed lead systems have been examined using computer models of the thorax to determine the extent to which they satisfy the fundamental conditions for corrected orthogonal leads. Under uniform, homogeneous, and bounded conditions, Brody and Arzbaecher (1964) evaluated the lead fields for several VCG systems and compared the degree of uniformity. They found that the Frank, SVEC III, and McFee-Parungao lead systems introduced a degree of distortion. However, the Grishman cube and Wilson tetrahedron lead systems were considerably worse. The McFee-
Parungao system was found to have the best orthogonality of all systems, but the strength of the leads was found to be unequal. Macfarlane (1969) introduced a modification that equalized the lead strengths.
Under uniform, homogeneous, and bounded conditions, Brody and Arzbaecher (1964) evaluated the lead fields for several VCG systems and compared the degree of uniformity. They found that the Frank, SVEC III, and McFee-Parungao lead systems introduced a degree of distortion. However, the Grishman cube and Wilson tetrahedron lead systems were considerably worse. The McFee-
Parungao system was found to have the best orthogonality of all systems, but the strength of the leads was found to be unequal. Macfarlane (1969) introduced a modification that equalized the lead strengths.
 The effect of inhomogeneities on the lead vector field has been considered by Milan Horá ek (1989). This examination was conducted by a computer simulation in which the influence of inhomogeneities on the image surface was evaluated.
The effect of inhomogeneities on the lead vector field has been considered by Milan Horá ek (1989). This examination was conducted by a computer simulation in which the influence of inhomogeneities on the image surface was evaluated.
 The effect of the intracavitary blood mass tends to counteract that of the lungs. The blood mass decreases tangential dipoles and enhances normal dipoles. The effect of lung conductivity on lead vectors was studied by Stanley, Pilkington, and Morrow (1986). Using a realistic canine torso model, they showed that the z (foot-to-head) dipole moment decreased monotonically as the lung conductivity increased. On the other hand, the y (right-to-left) and x (back-to-front) dipole moment have a bellshaped behavior, with low values for both high and low lung conductivities. They found that the lung conductivity, nevertheless, has relatively little effect on the overall torso volume conductor properties. The inhomogeneity that, in their study, has a significant effect is the skeletal muscle layer. These results are reasonably consistent with those of Gulrajani and Mailloux (1983) and Rudy and Plonsey (1980).
The effect of the intracavitary blood mass tends to counteract that of the lungs. The blood mass decreases tangential dipoles and enhances normal dipoles. The effect of lung conductivity on lead vectors was studied by Stanley, Pilkington, and Morrow (1986). Using a realistic canine torso model, they showed that the z (foot-to-head) dipole moment decreased monotonically as the lung conductivity increased. On the other hand, the y (right-to-left) and x (back-to-front) dipole moment have a bellshaped behavior, with low values for both high and low lung conductivities. They found that the lung conductivity, nevertheless, has relatively little effect on the overall torso volume conductor properties. The inhomogeneity that, in their study, has a significant effect is the skeletal muscle layer. These results are reasonably consistent with those of Gulrajani and Mailloux (1983) and Rudy and Plonsey (1980).
 Jari Hyttinen analyzed the properties of Frank, axial, and SVEC III lead systems with his computer model called the hybrid model (Hyttinen, 1989). He analyzed the magnitude and the direction of the lead vectors in various regions of the heart in an inhomogeneous thorax model. He also conducted studies on the sensitivities of the leads to sources in radial and tangential directions (in relation to the heart), which has certain clinical implications.
Jari Hyttinen analyzed the properties of Frank, axial, and SVEC III lead systems with his computer model called the hybrid model (Hyttinen, 1989). He analyzed the magnitude and the direction of the lead vectors in various regions of the heart in an inhomogeneous thorax model. He also conducted studies on the sensitivities of the leads to sources in radial and tangential directions (in relation to the heart), which has certain clinical implications.
 In his study of the ideal VCG lead, Hyttinen found that in all of the studied lead systems, the lead vectors of the x-leads are directed downward in the upper posterior part of the heart. The blood masses in and above the heart in the great vessels are mainly responsible for this behavior of the lead vectors. The x-lead, which is closest to ideal, is in the axial system. The total sensitivity in the x-direction is a little lower than that of the SVEC III x-lead, but the homogeneity of the lead is much better. The locations of the chest electrodes are good and the proximity effect is weaker in the axial x-lead compared to the other lead systems.
In his study of the ideal VCG lead, Hyttinen found that in all of the studied lead systems, the lead vectors of the x-leads are directed downward in the upper posterior part of the heart. The blood masses in and above the heart in the great vessels are mainly responsible for this behavior of the lead vectors. The x-lead, which is closest to ideal, is in the axial system. The total sensitivity in the x-direction is a little lower than that of the SVEC III x-lead, but the homogeneity of the lead is much better. The locations of the chest electrodes are good and the proximity effect is weaker in the axial x-lead compared to the other lead systems.
 For the y-leads, the SVEC III y-lead has the best properties. The SVEC III and the axial y-leads have equal sensitivity in the y-direction, but the differences in the spatial sensitivity distribution - that is, the homogeneity of the sensitivity - is better in the SVEC III system. The proximity effect is not so pronounced because of the use of lead I as a part of the SVEC III y-lead.
For the y-leads, the SVEC III y-lead has the best properties. The SVEC III and the axial y-leads have equal sensitivity in the y-direction, but the differences in the spatial sensitivity distribution - that is, the homogeneity of the sensitivity - is better in the SVEC III system. The proximity effect is not so pronounced because of the use of lead I as a part of the SVEC III y-lead.
 In the z-leads, the inhomogeneities are the main reasons for distortion of the spatial sensitivity. This can be seen especially in the septal area. The leads are, however, very similar with the Frank z-lead, having slightly better spatial sensitivity properties than the other lead systems..
In the z-leads, the inhomogeneities are the main reasons for distortion of the spatial sensitivity. This can be seen especially in the septal area. The leads are, however, very similar with the Frank z-lead, having slightly better spatial sensitivity properties than the other lead systems..
REFERENCES
Akulinichev IT (1956): Vectorelectrocardioscope. Voenno-Med. Zh. 1: 79. (In Russian).
Akulinichev IT (1960): Practical Questions in Vectorcardioscopy, Medgiz, Moscow. 214 p. (In Russian)
Brody DA, Arzbaecher RC (1964): A comparative analysis of several corrected vector-cardiographic leads. Circulation 29:(4, Suppl.) 533-45.
Duchosal PW, Sulzer R (1949): La Vectorcardiographie, S. Karger, New York, N.Y.
Fischmann EJ, Barber MR, Weiss GH (1971): Multielectrode grids which measure torso area and resistivity and yield dipole moments calibrated for these variables. In Proc. XIth Internat. Symp. On Vectorcardiography, New York, 1970, ed. I Hoffman, pp. 30-41, North-Holland Publishing Co., Amsterdam.
Frank E (1954): The image surface of a homogeneous torso. Am. Heart J. 47: 757-68.
Frank E (1956): An accurate, clinically practical system for spatial vectorcardiography. Circulation 13:(5) 737-49.
Grishman A, Scherlis L (1952): Spatial Vectorcardiography, 217 pp. Saunders, Philadelphia.
Gulrajani RM, Mailloux GE (1983): A simulation study of the effects of torso inhomogeneities on electrocardiographic potentials using realistic heart and torso models. Circ. Res. 52: 45-56.
Hollman W, Hollman HE (1939): Neue electrocardiographische Untersuchungsmethode. Z. Kreislaufforsch. 29: 546-558.
Horácek BM (1989): Lead theory. In Comprehensive Electrocardiology. Theory and Practice in Health and Disease, 1st ed. Vol. 1, ed. PW Macfarlane, TDV Lawrie, pp. 291-314, Pergamon Press, New York.
Horan LG, Flowers NC, Brody DA (1965): The interchangeability of vectorcardiographic systems. Am. Heart J. 70:(3) 365-76.
Hyttinen J (1989): Development of aimed ECG-leads. Tampere Univ. Tech., Tampere, Finland, Thesis, pp. 138. (Lic. Tech. thesis)
Kimura N (1939): Study on heart function by vectorcardiography of three-dimensional projection. Jpn. Circ. J. 5: 93.
Macfarlane PW (1969): A modified axial lead system for orthogonal lead electrocardiography. Cardiovasc. Res. 3:(10) 510-5.
Mann H (1920): A method for analyzing the electrocardiogram. Arch. Int. Med. 25: 283-94.
Mann H (1931): Interpretation of bundle-branch block by means of the monocardiogram. Am. Heart J. 6: 447-57.
Mann H (1938a): The monocardiogram. Stud. Rockefeller Inst. Med. Res. 109: 409-32.
Mann H (1938b): The monocardiograph. Am. Heart J. 15: 681-99.
McFee R, Parungao A (1961): An orthogonal lead system for clinical electrocardiography. Am. Heart J. 62: 93-100.
Milnor MR, Talbot SA, Newman EV (1953): A study of the relationship between unipolar leads and spatial vectorcardiograms, using the panoramic vectorcardiograph. Circulation 7: 545.
Nelson CV, Gastongay PR, Wilkinson AF, Voukydis PC (1971): A lead system for direction and magnitude of the heart vector. In Vectorcardiography 2. Proc. XIth Internat. Symp. On Vectorcardiography, New York, 1970, ed. I Hoffman, IR Hamby, E Glassman, pp. 85-97, North-Holland Publishing Co., Amsterdam.
Pawlov Z (1966): Über einige Fragen des Vektorkardiographischen Dreiflächensystems von Akulinitschev. In Neue Ergebnisse Der Elektrokardiologie, ed. E Schubert, (Proceedings of the 6th International Colloquium of Vectorcardiography, Leipzig 1965.), VEB Gustav Fischer Verlag, Jena.
Rudy Y, Plonsey R (1980): A comparison of volume conductor and source geometry effects on body surface and epicardial potentials. Circ. Res. 46:(2) 283-91.
Schellong F, Heller S, Schwingel G (1937): Das Vectorcardiogram; Eine Untersuchungsmethode des Herzens. Z. Kreislaufforsch. 29: 497-509.
Schmitt OH, Simonson E (1955): The present status of vectorcardiography. A.M.A. Arch. Internal Med. 96: 574-90.
Stanley PC, Pilkington TC, Morrow MN (1986): The effects of thoracic inhomogeneities on the relationship between epicardial and torso potentials. IEEE Trans. Biomed. Eng. BME-33:(3) 273-84.
Waller AD (1887): A demonstration on man of electromotive changes accompanying the heart's beat. J. Physiol. (Lond.) 8: 229-34.
Wenger R (1969): Klinische Vektorkardiographie, 2nd ed., Dr. Dietrich Steinkopff Verlag, Darmstadt.
Wilson FN, Johnston FD (1938): The vectorcardiogram. Am. Heart J. 16: 14-28.
Wilson FN, Johnston FD, Kossmann CE (1947): The substitution of a tetrahedron for the Einthoven triangle. Am. Heart J. 33: 594-603.
REFERENCES, BOOKS
Macfarlane PW, Lawrie TDV (eds.) (1989): Comprehensive Electrocardiology: Theory and Practice in Health and Disease. 1st ed. Vols. 1, 2, and 3. Pergamon Press, New York. 1785 p.



