20.1 INTRODUCTION
The first biomagnetic signal to be detected was the magnetocardiogram (MCG) by Baule and McFee (1963). The discovery raised a lot of optimism, as it was believed that MCG would provide as much new information about the heart's electric activity as had the ECG. Though this has been shown theoretically (Rush, 1975) and in practical clinical studies not to be true, there are still many potential clinical applications of the MCG. For instance, as will be discussed in Section 20.7, according to the present understanding, with the combined use of the ECG and the MCG, called electromagnetocardiogram, (EMCG), in some cardiac diseases the number of incorrectly diagnosed patients can be decreased by one half of that when using only the ECG is used. Since the concept of the magnetic heart vector was introduced by Baule and McFee in 1970, studies have been conducted to detect the vectormagnetocardiogram (i.e., in which the heart is considered as a magnetic dipole). Though the detection of the magnetic heart vector is an obvious selection as the first clinical tool, many of the MCG studies of today have been made by mapping the normal component of the magnetic field of the heart around the thorax.
Since the concept of the magnetic heart vector was introduced by Baule and McFee in 1970, studies have been conducted to detect the vectormagnetocardiogram (i.e., in which the heart is considered as a magnetic dipole). Though the detection of the magnetic heart vector is an obvious selection as the first clinical tool, many of the MCG studies of today have been made by mapping the normal component of the magnetic field of the heart around the thorax.
 There exist also many other kinds of trials for finding out clinical applications for the MCG - for example, testing the risk for sudden cardiac death and for rejection of an implanted heart. The localization of arrhythmogenic centers has also been a subject of intensive research. An overview of the methods for solving the biomagnetic inverse problem can be found in Swithenby (1987).
There exist also many other kinds of trials for finding out clinical applications for the MCG - for example, testing the risk for sudden cardiac death and for rejection of an implanted heart. The localization of arrhythmogenic centers has also been a subject of intensive research. An overview of the methods for solving the biomagnetic inverse problem can be found in Swithenby (1987).
 The main purpose of this chapter is to discuss the lead systems currently being applied in detecting the equivalent magnetic dipole of the heart, and to discuss briefly the ECG-MCG relationship.
The main purpose of this chapter is to discuss the lead systems currently being applied in detecting the equivalent magnetic dipole of the heart, and to discuss briefly the ECG-MCG relationship.
Table 17.1 (Section 17.4) lists several source and conductor models, tacitly assumed in various electrocardiographic lead systems. From that table, one can see that in present clinical electrocardiography (standard 12-lead system and Frank vectorelectrocardiography (VECG)), a dipole with a fixed location is used as the model of the cardiac electric source. The volume conductor is modeled either with the trivial solution (i.e., a homogeneous unbounded or spherical boundary) in the 12-lead ECG or with a finite (realistic), homogeneous conductor in the Frank VECG.
In electrocardiography, the mapping of the distribution of the electric potential on the surface of the thorax has been applied since the first detection of the human electrocardiogram by Augustus Waller in 1887 (see Figure 1.4). It has, however, not come into clinical use but has remained primarily as a research tool.
In the following discussion we assume that the heart is a spherical conducting region between the insulating lungs. For the XYZ and ABC lead systems it would be enough to assume cylindrical symmetry for each three component, which leads to a spherically symmetric volume conductor for the three orthogonal measurements. The y and z components of the unipositional lead system require, however, an assumption of a conducting spherical heart region inside the insulating lungs. This assumption forces the lead fields to flow tangentially within the heart region. This is called a self-centering effect (Baule and McFee, 1970). This is also an anatomically realistic assumption.
20.2 BASIC METHODS IN MAGNETOCARDIOGRAPHY
20.2.1 Measurement of the equivalent magnetic dipole
PRECONDITIONS:
SOURCE: Magnetic dipole in a fixed location
CONDUCTOR: Finite, homogeneous (or possibly inhomogeneous)
 Magnetocardiography was intended, at least initially, to complement the electric measurements of the heart's electric activity, or possibly replace it (e.g., in screening tests). It is therefore natural to select source and conductor models for magnetocardiography that are on the same level of complexity as for electrocardiography. This means that in clinical applications the obvious selection for the source model is the magnetic dipole. The accuracy of the conductor model may vary, but because of the self-centering effect of the well-conducting heart muscle and intracardiac blood mass (Baule and McFee, 1970) none of the extra arrangements required in the finite, inhomogeneous model are needed.
Magnetocardiography was intended, at least initially, to complement the electric measurements of the heart's electric activity, or possibly replace it (e.g., in screening tests). It is therefore natural to select source and conductor models for magnetocardiography that are on the same level of complexity as for electrocardiography. This means that in clinical applications the obvious selection for the source model is the magnetic dipole. The accuracy of the conductor model may vary, but because of the self-centering effect of the well-conducting heart muscle and intracardiac blood mass (Baule and McFee, 1970) none of the extra arrangements required in the finite, inhomogeneous model are needed.
 As a consequence, a magnetocardiographic signal includes three components which may be displayed either in scalar form as a function of time, or in the form of vector loops (one lead as a function of another). The selection of the display is of secondary importance (Baule and McFee, 1970: Malmivuo, 1976, 1980, 1981). The selection of the magnetic heart vector as the basis of the clinical MCG system is further explained in Figure 20.1.
As a consequence, a magnetocardiographic signal includes three components which may be displayed either in scalar form as a function of time, or in the form of vector loops (one lead as a function of another). The selection of the display is of secondary importance (Baule and McFee, 1970: Malmivuo, 1976, 1980, 1981). The selection of the magnetic heart vector as the basis of the clinical MCG system is further explained in Figure 20.1.

Fig. 20.1 Selection of the magnetic dipole as the basis of the clinical magnetocardiographic measurement system.
20.2.2 The magnetic field mapping method
PRECONDITIONS:
SOURCE: Distribution of  i
i
CONDUCTOR: Infinite, homogeneous
 Similarly, in magnetocardiography, the mapping of the magnetic field around the thorax has been a research tool. Though the magnetic field is a vector quantity and has therefore three components at each location in space, the mapping method has usually been applied for registering only one component (the x-component) of the magnetic field around the thorax. The mapping has usually been done on a certain grid. Such grids were first introduced by Cohen and McCaughan (1972). The most popular grid, introduced by Malmivuo, Saarinen, and Siltanen (1973), includes 6×6 measurement locations on the anterior thoracic wall. Later, the anatomic measures of this grid were defined in more detail; this grid became known as the "standard grid" (Karp, 1981).
Similarly, in magnetocardiography, the mapping of the magnetic field around the thorax has been a research tool. Though the magnetic field is a vector quantity and has therefore three components at each location in space, the mapping method has usually been applied for registering only one component (the x-component) of the magnetic field around the thorax. The mapping has usually been done on a certain grid. Such grids were first introduced by Cohen and McCaughan (1972). The most popular grid, introduced by Malmivuo, Saarinen, and Siltanen (1973), includes 6×6 measurement locations on the anterior thoracic wall. Later, the anatomic measures of this grid were defined in more detail; this grid became known as the "standard grid" (Karp, 1981).
 In lead field theory, it may be shown that lead systems used in mapping often introduce a distortion of the signal that necessarily originates from the inhomogeneities of the volume conductor. (The situation is the same as in mapping the electric potential field.) Some of these magnetic measurements may also be realized with a similar sensitivity distribution by use of electric measurements with a higher signal-to-noise ratio and with easier application (Figure 20.2).
In lead field theory, it may be shown that lead systems used in mapping often introduce a distortion of the signal that necessarily originates from the inhomogeneities of the volume conductor. (The situation is the same as in mapping the electric potential field.) Some of these magnetic measurements may also be realized with a similar sensitivity distribution by use of electric measurements with a higher signal-to-noise ratio and with easier application (Figure 20.2).
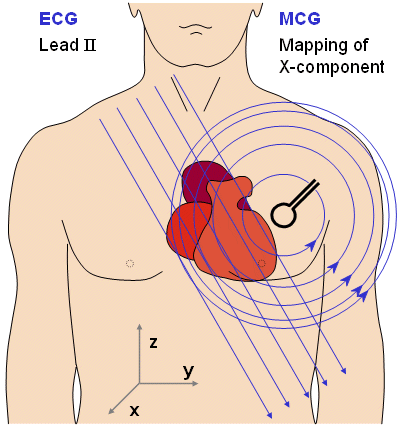
Fig. 20.2 The similarity between the lead fields of certain electric and magnetic leads are illustrated. If the magnetic field is measured in such an orientation (in the x direction in this example) and location, that the symmetry axis is located far from the region of the heart, the magnetic lead field in the heart's region is similar to the electric lead field of a lead (lead II in this example), which is oriented normal to the symmetry axis of the magnetic lead. This similarity may also be verified from the similarity of the corresponding detected signals.
20.2.3 Other methods of magnetocardiography
In addition to the analysis of the parameters of the MCG signals, recorded either by determining the equivalent magnetic dipole or by the mapping method, several other techniques have also been applied. Of these the localization of cardiac sources is briefly discussed here.
 The localization of cardiac electric sources is a highly desired objective since it may enable the localization of cardiac abnormalities including those of abnormal conduction pathways. These may cause dangerous arrhythmias or contribute to a reduction in cardiac performance. Abnormal conduction pathways, for example, conduct electric activity from the atrial muscle directly to the ventricular muscle, bypassing the AV junction. This is called the Wolff-Parkinson-White or (WPW) syndrome. If a retrograde conduction pathway also exists from the ventricular mass back to the atrial mass, this re-entry path may result in tachycardia. If the symptoms due to this abnormal conduction do not respond to drugs, then the tissue forming the abnormal pathway must be removed surgically, hence requiring prior localization.
The localization of cardiac electric sources is a highly desired objective since it may enable the localization of cardiac abnormalities including those of abnormal conduction pathways. These may cause dangerous arrhythmias or contribute to a reduction in cardiac performance. Abnormal conduction pathways, for example, conduct electric activity from the atrial muscle directly to the ventricular muscle, bypassing the AV junction. This is called the Wolff-Parkinson-White or (WPW) syndrome. If a retrograde conduction pathway also exists from the ventricular mass back to the atrial mass, this re-entry path may result in tachycardia. If the symptoms due to this abnormal conduction do not respond to drugs, then the tissue forming the abnormal pathway must be removed surgically, hence requiring prior localization.
 In clinical practice the conduction pathways are at present localized invasively with a catheter in an electrophysiological study, which may last several hours. This time may be shortened by first making an initial noninvasive localization of the equivalent source of the conduction pathway from the electric potentials on the surface of the thorax. A review of these methods is published by Gulrajani, Savard, and Roberge (1988).
In clinical practice the conduction pathways are at present localized invasively with a catheter in an electrophysiological study, which may last several hours. This time may be shortened by first making an initial noninvasive localization of the equivalent source of the conduction pathway from the electric potentials on the surface of the thorax. A review of these methods is published by Gulrajani, Savard, and Roberge (1988).
 In magnetocardiographic localization the goal is to introduce an alternative to the electric localization using the magnetic methods. Utilization of this complementary technique may improve the overall localization accuracy. The magnetocardiographic localization is usually made by mapping the x component of the cardiac magnetic field at 30-40 locations on the anterior surface of the thorax with consecutive measurements using a single-channel magnetometer or simultaneously using a multichannel magnetometer. The dipole model is the most obvious to use as a source model for the localization methods. It has been shown that with the addition of the quadrupolar model, the accuracy of localization may be increased (Nenonen et al., 1991a). The accuracy of the magnetocardiographic localization depends to a great extent on the accuracy of the volume conductor model applied (Nenonen et al., 1991b). The accuracy of the magnetocardiographic localization of the origin of an abnormal conduction pathway is of the order of 2-3 cm. Because magnetocardiographic localization has been shown to have greater complexity and costs as compared to the electric method, the magnetic method does not, at present, compete with the electric method in clinical practice.
In magnetocardiographic localization the goal is to introduce an alternative to the electric localization using the magnetic methods. Utilization of this complementary technique may improve the overall localization accuracy. The magnetocardiographic localization is usually made by mapping the x component of the cardiac magnetic field at 30-40 locations on the anterior surface of the thorax with consecutive measurements using a single-channel magnetometer or simultaneously using a multichannel magnetometer. The dipole model is the most obvious to use as a source model for the localization methods. It has been shown that with the addition of the quadrupolar model, the accuracy of localization may be increased (Nenonen et al., 1991a). The accuracy of the magnetocardiographic localization depends to a great extent on the accuracy of the volume conductor model applied (Nenonen et al., 1991b). The accuracy of the magnetocardiographic localization of the origin of an abnormal conduction pathway is of the order of 2-3 cm. Because magnetocardiographic localization has been shown to have greater complexity and costs as compared to the electric method, the magnetic method does not, at present, compete with the electric method in clinical practice.
20.3 METHODS FOR DETECTING THE MAGNETIC HEART VECTOR
20.3.1 The source and conductor models and the basic form of the lead system for measuring the magnetic dipole
PRECONDITIONS:
SOURCE: Distribution of  i forming a volume source (at the origin)
i forming a volume source (at the origin)
CONDUCTOR: Finite, spherical, homogeneous: spherical conducting heart region inside insulating lung region
 Earlier, in Section 12.5 it was stated that, by definition, the magnetic dipole moment of a volume current distribution
Earlier, in Section 12.5 it was stated that, by definition, the magnetic dipole moment of a volume current distribution  i in an infinite, homogeneous volume conductor with respect to an arbitrary origin is defined as (Stratton, 1941):
i in an infinite, homogeneous volume conductor with respect to an arbitrary origin is defined as (Stratton, 1941):
 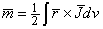 | (20.1) |
 Similarly, as stated further in Section 12.5, in an infinite, homogeneous volume conductor, the magnetic dipole moment of an impressed current density distribution
Similarly, as stated further in Section 12.5, in an infinite, homogeneous volume conductor, the magnetic dipole moment of an impressed current density distribution  i is represented by the first term on the right side of Equation 12.25:
i is represented by the first term on the right side of Equation 12.25:
 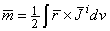 | (20.2) |
 Section 12.6 showed that the lead system that detects this magnetic dipole moment has three orthogonal components. Each component produces, when energized with the reciprocal current, a linear, homogeneous, reciprocal magnetic field
Section 12.6 showed that the lead system that detects this magnetic dipole moment has three orthogonal components. Each component produces, when energized with the reciprocal current, a linear, homogeneous, reciprocal magnetic field  LM over the source region. These reciprocal magnetic fields induce lead fields
LM over the source region. These reciprocal magnetic fields induce lead fields  LM in which the lead current is directed tangentially, and its density is proportional to the distance from the symmetry axis, as illustrated in Figure 20.3.
LM in which the lead current is directed tangentially, and its density is proportional to the distance from the symmetry axis, as illustrated in Figure 20.3.
 Furthermore, Section 12.7 showed that a natural method to realize such a lead system is to make either unipolar or bipolar measurements on the coordinate axes (Malmivuo, 1976), as described in Figure 20.4..
Furthermore, Section 12.7 showed that a natural method to realize such a lead system is to make either unipolar or bipolar measurements on the coordinate axes (Malmivuo, 1976), as described in Figure 20.4..

- Fig. 20.3 (A) One component of the reciprocal magnetic field LM and
 (B) one component of the lead field LM of an ideal lead system detecting the magnetic dipole moment of a volume source. Three such orthogonal components form the complete lead system.
(B) one component of the lead field LM of an ideal lead system detecting the magnetic dipole moment of a volume source. Three such orthogonal components form the complete lead system.
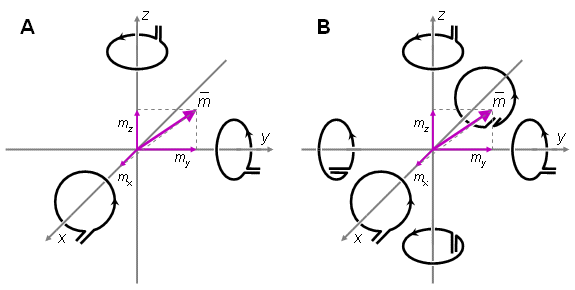
- Fig. 20.4 A natural method to measure the magnetic dipole moment of a source locating in the origin is to measure the x-, y-, and z-components of the magnetic field on corresponding coordinate axes. These may be either (A) unipolar or (B) bipolar measurements.
20.3.2 Baule-McFee lead system
The first description of the concept of the magnetic heart vector and of the principle for its measurement was given by Gerhard M. Baule and Richard McFee in 1970. In the same article (Baule and McFee, 1970) the authors introduced a device for measuring the magnetic field of the heart. Their system is described in Figure 20.5. The lead system was designed for induction-coil magnetometers using ferromagnetic cores rather than for magnetometers using the SQUID (which did not exist at that time). The lead system was designed to utilize a combination of ten coils to make bipolar measurements of the three orthogonal components of the magnetic heart vector simultaneously.
The lead system was designed for induction-coil magnetometers using ferromagnetic cores rather than for magnetometers using the SQUID (which did not exist at that time). The lead system was designed to utilize a combination of ten coils to make bipolar measurements of the three orthogonal components of the magnetic heart vector simultaneously.
 Figure 20.5A describes the general construction of the ferromagnetic core system of magnodes. The principle for the measurement of the x component is illustrated in Figure 20.5B. In this measurement the magnodes in the center of the ferromagnetic cores are utilized. This figure shows the generation of the reciprocal magnetic field in the direction of the x axis within the region of the heart. When one replaces the reciprocal current generator with an amplifier, it is, according to the lead field theory, possible to detect the x component of the magnetic heart vector. The principle for the measurement of the y component is illustrated in Figure 20.5C. This figure shows the generation of the reciprocal magnetic field in the direction of the y axis within the region of the heart. The detection of the z component is realized with a similar circuit of coils located with the other two pairs of magnodes in the z direction, as illustrated in Figure 20.5D.
Figure 20.5A describes the general construction of the ferromagnetic core system of magnodes. The principle for the measurement of the x component is illustrated in Figure 20.5B. In this measurement the magnodes in the center of the ferromagnetic cores are utilized. This figure shows the generation of the reciprocal magnetic field in the direction of the x axis within the region of the heart. When one replaces the reciprocal current generator with an amplifier, it is, according to the lead field theory, possible to detect the x component of the magnetic heart vector. The principle for the measurement of the y component is illustrated in Figure 20.5C. This figure shows the generation of the reciprocal magnetic field in the direction of the y axis within the region of the heart. The detection of the z component is realized with a similar circuit of coils located with the other two pairs of magnodes in the z direction, as illustrated in Figure 20.5D.
 The lead system of Baule and McFee was never realized because it would have been disturbed by ambient magnetic noise to such an extent that it would have been unable to detect the MCG. Its main purpose was to demonstrate one possible option for detecting the magnetic heart vector.
The lead system of Baule and McFee was never realized because it would have been disturbed by ambient magnetic noise to such an extent that it would have been unable to detect the MCG. Its main purpose was to demonstrate one possible option for detecting the magnetic heart vector.

Fig. 20.5 Baule-McFee lead system.
 (A) The general construction of the measurement system.
(A) The general construction of the measurement system.
 (B) Measurement of the x-component of the magnetic heart vector.
(B) Measurement of the x-component of the magnetic heart vector.
 (C) Measurement of the y-component of the magnetic heart vector.
(C) Measurement of the y-component of the magnetic heart vector.
 (D) Measurement of the z-component of the magnetic heart vector.
(D) Measurement of the z-component of the magnetic heart vector.
 Baule-McFee lead system makes a bipolar measurement of the equivalent magnetic dipole of the heart.
Baule-McFee lead system makes a bipolar measurement of the equivalent magnetic dipole of the heart.20.3.3 XYZ lead system
The magnetic lead system illustrated in Figure 20.4 was first applied to magnetocardiography by Malmivuo (1976). This method, which is called the XYZ lead system, is further described in Figure 20.6. The symmetric bipolar form of the XYZ lead system is shown in this figure. Each of the three components are measured symmetrically (i.e., on both sides of the source). This method has the drawback that measurement of the component along the z axis (foot-to-head axis) of the body is very difficult. Also, in the measurement along the y axis (right-to-left axis) the detectors must be placed quite far from the source.
 The symmetric (bipolar) XYZ lead system requires six magnetometers or six consecutive measurements with one magnetometer. If the measurements are made nonsymmetrically (unipolarly) on only one side of the body (on positive coordinate axes), three magnetometers or consecutive measurements are needed. The latter arrangement increases the signal amplitude owing to the shorter measurement distance, but decreases the quality of the lead field due to the unipolar measurement.
The symmetric (bipolar) XYZ lead system requires six magnetometers or six consecutive measurements with one magnetometer. If the measurements are made nonsymmetrically (unipolarly) on only one side of the body (on positive coordinate axes), three magnetometers or consecutive measurements are needed. The latter arrangement increases the signal amplitude owing to the shorter measurement distance, but decreases the quality of the lead field due to the unipolar measurement.
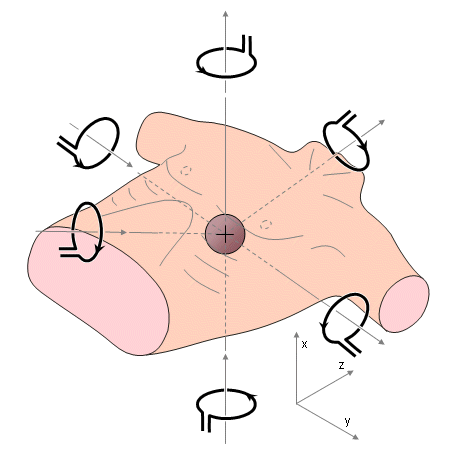
Fig. 20.6 Symmetric XYZ lead system. The bipolar arrangement provides good lead field uniformity. The difficulty arises in locating all magnetometers in their correct position surrounding the body.
20.3.4 ABC lead system
Malmivuo (1976) proposed a method to avoid the difficulties encountered in the application of the XYZ lead system. If the three orthogonal coordinate axes are chosen to coincide with the edges of a cube, in which the diagonal is the x axis (back-to-front axis) and the corner is located in the center of the heart, we obtain a coordinate system that is oriented more symmetrically in relation to the body. This coordinate system is called the ABC coordinate system and is shown in Appendix A.
 The ABC lead system is obtained from the XYZ lead system by aligning the magnetometers along the ABC coordinates. Figure 20.7 illustrates the ABC lead system in its symmetric (bipolar) form. The ABC lead system may also be applied nonsymmetrically (unipolarly) by conducting measurements only on the anterior side of the thorax. In this case the measurements can be made much closer to the heart, thus increasing the signal-to-noise ratio. However, in this case the quality of the lead fields decreases, as they are less uniform throughout the heart.
The ABC lead system is obtained from the XYZ lead system by aligning the magnetometers along the ABC coordinates. Figure 20.7 illustrates the ABC lead system in its symmetric (bipolar) form. The ABC lead system may also be applied nonsymmetrically (unipolarly) by conducting measurements only on the anterior side of the thorax. In this case the measurements can be made much closer to the heart, thus increasing the signal-to-noise ratio. However, in this case the quality of the lead fields decreases, as they are less uniform throughout the heart.
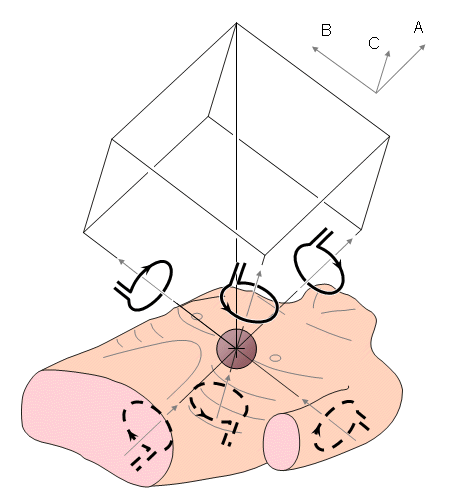
Fig. 20.7 The symmetric bipolar ABC lead system.
20.3.5 Unipositional lead system
In the application of SQUID magnetometry, the separate location of each magnetometer is considered a major deficiency owing to high cost of multiple magnetometers or increased measurement time when applying a single magnetometer consecutively in separate locations. In 1976 Malmivuo introduced a third lead system, called the unipositional lead system, which avoids the difficulty of multiple measurement locations. In its nonsymmetric (unipolar) form it is possible to realize this system with a single liquid helium dewar because the three coils (or gradiometer systems) are located at the same position. This is a significant improvement over the XYZ and ABC lead systems (Malmivuo, 1976). The fact that in addition to the x component, the y and z components of the magnetic heart vector may also be measured from the same location as the one where the x component is measured with the XYZ lead system, is based on the following theory (see Figure 20.8A):
 We divide the magnetic dipole
We divide the magnetic dipole 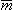 into three components, mx, my, and mz. We consider the three components Hx, Hy, and Hz of the magnetic field
into three components, mx, my, and mz. We consider the three components Hx, Hy, and Hz of the magnetic field  on the x axis due to this magnetic dipole
on the x axis due to this magnetic dipole 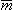 . From the magnetic field lines we recognize that the x component of the magnetic field (Hx) is in the same direction as the x component of the magnetic dipole (mx). The y and z components of the magnetic field are, however, parallel but opposite to the directions of the y and z components of the magnetic dipole, respectively. Furthermore, for mx, my, and mz of equal magnitude, the amplitudes of the components Hy and Hz of the magnetic field are one half that of the component Hx. This is a consequence of the equations of the magnetic field of a magnetic dipole (oriented in the z-direction) (see Figure 20.8B):
. From the magnetic field lines we recognize that the x component of the magnetic field (Hx) is in the same direction as the x component of the magnetic dipole (mx). The y and z components of the magnetic field are, however, parallel but opposite to the directions of the y and z components of the magnetic dipole, respectively. Furthermore, for mx, my, and mz of equal magnitude, the amplitudes of the components Hy and Hz of the magnetic field are one half that of the component Hx. This is a consequence of the equations of the magnetic field of a magnetic dipole (oriented in the z-direction) (see Figure 20.8B):
 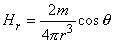 | |
 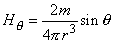 | (20.3) |
  |
| where | m | = the moment of the magnetic dipole |
| r | = radius vector (distance) | |
| θ | = the angle between the moment (z-axis) and the radius vector (polar or colatitude angle) | |
| φ | = the angle about the moment (z-axis) (azimuth angle). |
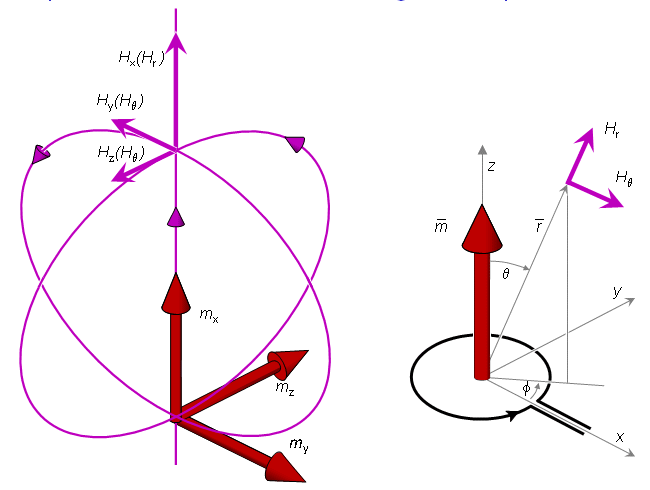
- Fig. 20.8 (A) The three components Hx, Hy, and Hz of the magnetic field
 due to the three components mx, my, and mz of a magnetic dipole
due to the three components mx, my, and mz of a magnetic dipole 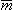 .
.
 (B) Components of the magnetic field of a dipole.
(B) Components of the magnetic field of a dipole.
 In the arrangement of Figure 20.8 the magnetic field component Hx corresponds to Hr, and components Hy and Hz correspond to Hθ of Equation 20.3.
In the arrangement of Figure 20.8 the magnetic field component Hx corresponds to Hr, and components Hy and Hz correspond to Hθ of Equation 20.3.
 The principle of the unipositional lead system may be similarly considered in terms of the lead field. We consider the reciprocal magnetic field due to feeding a reciprocal current Ir to the magnetometer coil (see Figure 20.9). The strength of the dipole moment for a single-turn coil can be found from Equation 20.4 (higher moments can apparently be ignored, if the field is at a large distance compared to the coil radius a):
The principle of the unipositional lead system may be similarly considered in terms of the lead field. We consider the reciprocal magnetic field due to feeding a reciprocal current Ir to the magnetometer coil (see Figure 20.9). The strength of the dipole moment for a single-turn coil can be found from Equation 20.4 (higher moments can apparently be ignored, if the field is at a large distance compared to the coil radius a):
 m = Iπa2 m = Iπa2 | (20.4) |
| where | I | = coil current |
| a | = coil radius |
(For N turns, m = Iπa2N.) The direction of
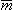 is normal to the plane of the coil.
is normal to the plane of the coil.
 In Figure 20.9A the magnetometer coil is oriented ( θ = 0° , 180° ) so, that its axis passes through the heart, whose center is locatied at the coordinate origin. This corresponds to the arrangement for measuring the x-component of the magnetic heart vector with the XYZ lead system. Now application of Equation 20.3 shows that the (reciprocal) magnetic field in the region of the heart is
In Figure 20.9A the magnetometer coil is oriented ( θ = 0° , 180° ) so, that its axis passes through the heart, whose center is locatied at the coordinate origin. This corresponds to the arrangement for measuring the x-component of the magnetic heart vector with the XYZ lead system. Now application of Equation 20.3 shows that the (reciprocal) magnetic field in the region of the heart is
 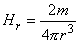 | (20.5) |
 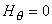 |
 Equation 20.3 again demonstrates that a magnetometer on the x-axis is sensitive to the same component of the magnetic heart dipole as corresponds to its own orientation. The aforementioned result is obtained only when the coil is at a sufficiently large distance from the heart compared to the extent of the heart so that, to a satisfactory approximation, all points in the heart (relative to an origin at the coil) are described by r = r, θ = 0° .
Equation 20.3 again demonstrates that a magnetometer on the x-axis is sensitive to the same component of the magnetic heart dipole as corresponds to its own orientation. The aforementioned result is obtained only when the coil is at a sufficiently large distance from the heart compared to the extent of the heart so that, to a satisfactory approximation, all points in the heart (relative to an origin at the coil) are described by r = r, θ = 0° .
 To measure the y component of the magnetic heart vector, the magnetometer coil is tilted 90°, whereupon points in the heart may be approximated by θ = 90°, 270°, as in Figure 20.9B (assuming, as before, that the distance to the heart is large compared to the extent of the heart). Consequently, the magnetic field in the heart's region is
To measure the y component of the magnetic heart vector, the magnetometer coil is tilted 90°, whereupon points in the heart may be approximated by θ = 90°, 270°, as in Figure 20.9B (assuming, as before, that the distance to the heart is large compared to the extent of the heart). Consequently, the magnetic field in the heart's region is
 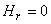 | (20.6) |
 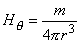 | (20.6) |
This equation is also obtained from Equation 20.3 based on the assumption that any point in the heart has the coordinate (r = r, θ = 90° ). It again demonstrates that the magnetometer is sensitive to the magnetic dipole component of the heart in the same direction as the magnetometer axis (although, in this case, opposite to it). The situation for measuring the z component follows a similar argument.
 We note that the intensity of the reciprocal magnetic field in the former case (x component) is exactly twice that in the latter case (y and z component). Furthermore, in the former case, the reciprocal magnetic field orientation is the same as the direction of the dipole moment of the reciprocally energized coil. In the second case, the reciprocal magnetic field direction is opposite to the direction of the dipole moment of the coil. Therefore, when one is using the unipositional lead system, the two nonaxial components (y and z) of the magnetic heart vector (MHV) are obtained from the magnetic field vector (MFV; the uncorrected lead signal from the mutually perpendicular magnetometer coils) by multiplying by a factor of -2, as shown in Equation 20.7. Figure 20.10 illustrates the realization of the unipositional lead system.
We note that the intensity of the reciprocal magnetic field in the former case (x component) is exactly twice that in the latter case (y and z component). Furthermore, in the former case, the reciprocal magnetic field orientation is the same as the direction of the dipole moment of the reciprocally energized coil. In the second case, the reciprocal magnetic field direction is opposite to the direction of the dipole moment of the coil. Therefore, when one is using the unipositional lead system, the two nonaxial components (y and z) of the magnetic heart vector (MHV) are obtained from the magnetic field vector (MFV; the uncorrected lead signal from the mutually perpendicular magnetometer coils) by multiplying by a factor of -2, as shown in Equation 20.7. Figure 20.10 illustrates the realization of the unipositional lead system.
 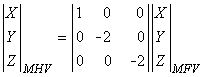 | (20.7) |
| where | MHV | = magnetic heart vector |
| MFV | = magnetic field vector |
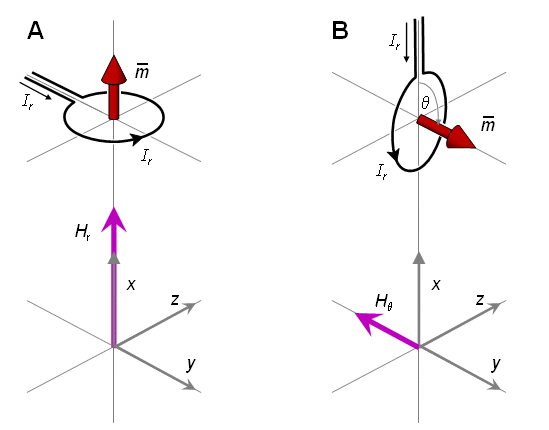
- Fig. 20.9 Generation of the reciprocal magnetic field in the heart's region when measuring
 (A) the x component and
(A) the x component and
 (B) the y component of the magnetic heart vector with the unipositional lead system.
(B) the y component of the magnetic heart vector with the unipositional lead system.
 The situation in the measurement of the z component is similar to that in the measurement of the y component.
The situation in the measurement of the z component is similar to that in the measurement of the y component.
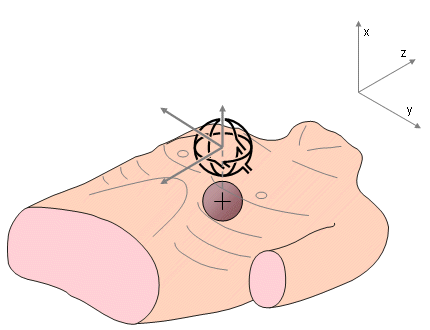
- Fig. 20.10 Realization of the unipositional lead system. The arrows indicate the measurement direction. The shaded sphere represents the heart.
Corrected unipositional lead system
Eskola and Malmivuo proposed an improved version of the nonsymmetric unipositional lead system in 1983 (Eskola, 1983; Eskola and Malmivuo, 1983). Model experiments showed that in the unipolar measurement situation, a more accurate result is obtained when the factor of -2 in the nonaxial components is replaced by a factor -1 (as illustrated in Equation 20.8). This modification is explained by the proximity effect (see the next section), the boundary at the thorax, and the way in which internal inhomogeneities affect the lead fields in the nonsymmetric measurement situation:
 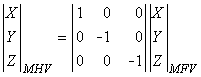 | (20.8) |
| where | MHV | = magnetic heart vector |
| MFV | = magnetic field vector |
 These model experiments also evaluated the optimum location for the measurement. It was found that the distortion of the lead field was smallest when the magnetometer is placed at the fourth left intercostal space at the sternal edge, corresponding to the location of V2 in the standard 12-lead ECG. This measurement position, shown in Figure 20.11, is also easy to locate.
These model experiments also evaluated the optimum location for the measurement. It was found that the distortion of the lead field was smallest when the magnetometer is placed at the fourth left intercostal space at the sternal edge, corresponding to the location of V2 in the standard 12-lead ECG. This measurement position, shown in Figure 20.11, is also easy to locate.
Symmetric unipositional lead system
As in the XYZ and ABC lead systems, the quality of the lead fields of the unipositional lead system can be considerably improved with a symmetric (bipolar) measurement arrangement. In the symmetric unipositional lead system, measurements are made on both sides of the heart, at the same distance from the center of the heart on the line parallel to the x axis, at the same location as shown in Figure 20.11 for the nonsymmetric unipositional system. Then the signals for the x, y, and z components are averaged with correct sign convention as is done in the symmetric XYZ and ABC lead systems as well. In the symmetric unipositional lead system, Equation 20.7 is valid because the magnetometer on the anterior side is located further from the heart and because the distortion in the lead field is to a high degree compensated by the symmetry (see Figure 20.16). The realization of the symmetric unipositional system is shown in Figure 20.12.
In the symmetric unipositional lead system, Equation 20.7 is valid because the magnetometer on the anterior side is located further from the heart and because the distortion in the lead field is to a high degree compensated by the symmetry (see Figure 20.16). The realization of the symmetric unipositional system is shown in Figure 20.12.
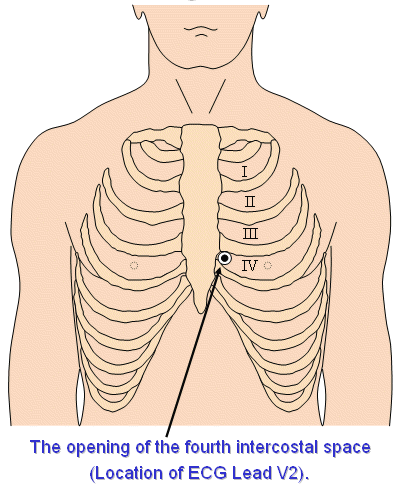
- Fig. 20.11 Measurement location of the unipositional lead system is at the fourth left intercostal space at the sternal edge (the same location as for electrocardiographic precordial lead V2 ).
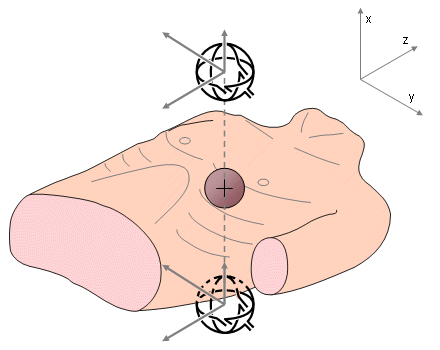
- Fig. 20.12 Realization of the symmetric unipositional lead system.
20.4 SENSITIVITY DISTRIBUTION OF BASIC MCG LEADS
20.4.1 Heart and thorax models and the magnetometer
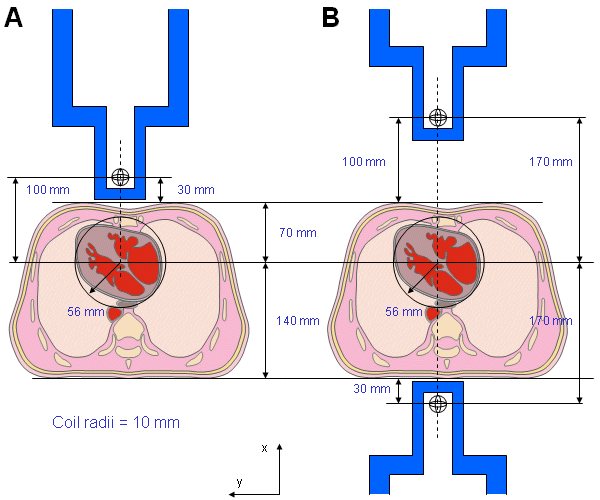
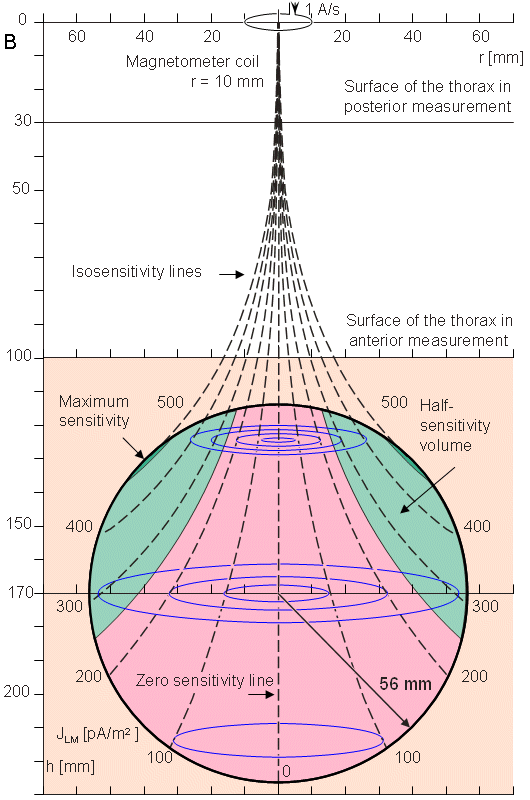
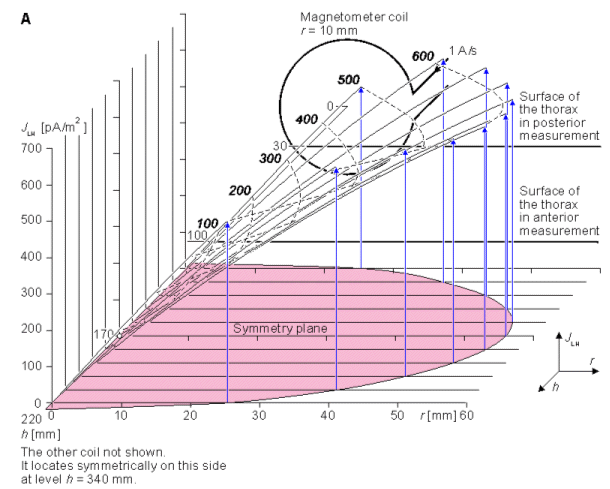
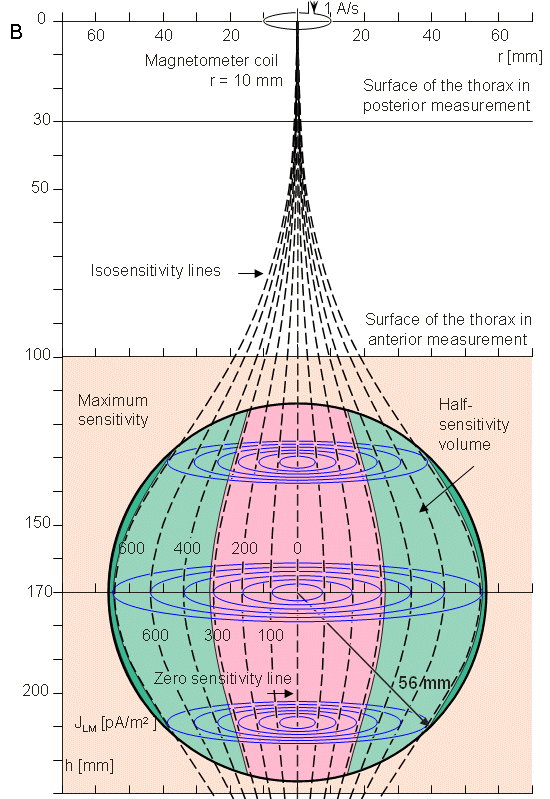
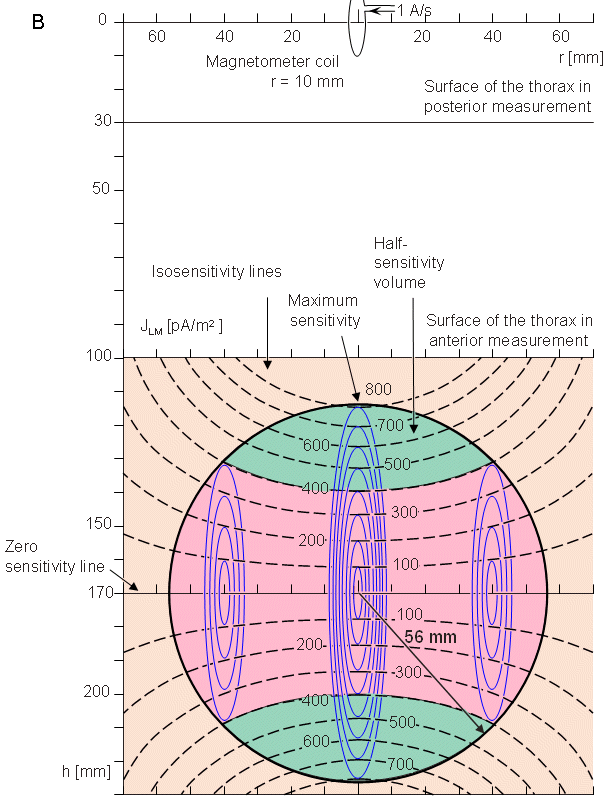
In this section, the sensitivity distribution of a single-coil magnetometer is calculated according to Section 12.11. The sensitivity distribution is calculated for the cylindrically symmetric situation. We assume that the antero-posterior dimension of the thorax is 210 mm and that the radius of the spherical heart model is 56 mm, as shown in Figure 20.13. The center of the heart is located 70 mm behind the anterior chest wall and 140 mm in front of the posterior chest wall. We further assume that the magnetometer coil radius is 10 mm and the distance from its center to the chest wall is 30 mm. Thus, when the magnetometer is located at the anterior or posterior side of the thorax, the minimum distance from the center of the magnetometer coil to the center of the heart is 100 mm or 170 mm, respectively (Malmivuo, 1976). These measures correspond to the unipolar and bipolar unipositional measurements. In this section it is assumed that the magnetometer does not have the compensation coils, i.e., the magnetometer is not a gradiometer.
Fig. 20.13 Dimensions for the thorax and heart models and the measurement distances in unipolar and bipolar unipositional measurements.
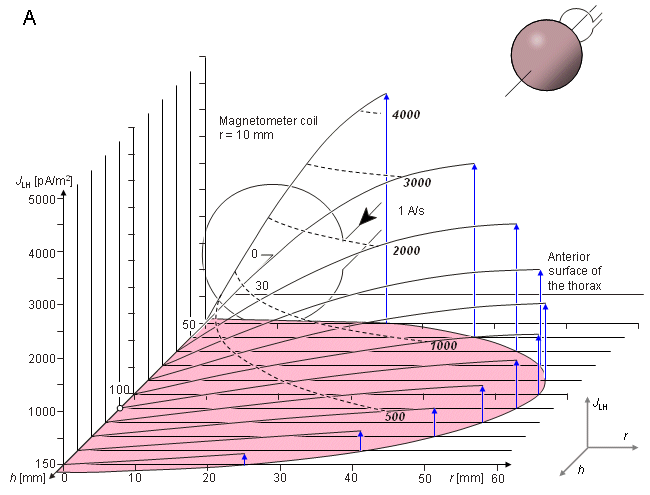
Fig. 20.14 Sensitivity distribution of a unipolar (nonsymmetric) measurement within the region of the spherical heart model for a 100 mm magnetometer - heart center separation. The figure also illustrates the location and size of the magnetometer. This measurement situation corresponds to the measurement of the x component of the MHV with the nonsymmetric unipositional lead system in the anterior side of the thorax.
Fig. 20.15 The sensitivity distribution of a unipolar (nonsymmetric) measurement within the region of the spherical heart model for a 170 mm magnetometer - heart center separation. This measurement situation corresponds to the measurement of the x component of the MHV at the posterior side of the thorax.
Fig. 20.16 Sensitivity distribution of a bipolar (symmetric) measurement within the region of the spherical heart model. The figure also illustrates the anterior magnetometer. This measurement situation corresponds to the measurement of the x component of the MHV with the symmetric XYZ lead system or with the symmetric unipositional lead system with measurements on both sides of the thorax.
Fig. 20.17 Sensitivity distribution in the measurement of the y component with the symmetric unipositional lead system illustrated
(A) in the zx plane and (B) in the yz plane. Isosensitivity lines are illustrated with black dashed lines. Lead field current flow lines are sketched with blue solid lines.
Though the unipositional MCG measurement is made at only one location compared to the 30-40 measurement locations of the mapping method, the diagnostic performance of the unipositional VMCG method is at least as good as that of the mapping system.
There is no significant difference between the diagnostic performance of the MCG compared to Frank's ECG.
The diagnostic classifications of ECG and MCG are dissimilar. (This means that the individual subjects classified in each group are not the same with both methods even though the number of the correctly diagnosed patients are the same.)
The diagnostic performance of the EMCG is better than that of the ECG or MCG alone, even though the EMCG uses the same total number of parameters as in either the ECG or the MCG. At its best, the EMCG, by combining electric and magnetic data, could reduce the number of patients classified incorrectly to about one half.
Fig. 20.23 Illustration of the principle by which the diagnostic performance may be increased by use of biomagnetic measurements.
The MCG measures the electric activity of the heart muscle. Therefore, on grounds of cost-effectiveness, if only one of these methods is used when such recordings can be done electrically, the ECG should be used unless there are technical reasons for selecting the MCG (e.g., in screening tests, in patients with skin burns, in recording DC fields, etc.).
The ECG measures the electric potential field, which is a scalar field. Therefore, one measurement at each measurement location is enough. The MCG measures the magnetic field, which is a vector field. Therefore, MCG measurements should provide a vector description - that is, three orthogonal measurements at each measurement location - to get all available information (Malmivuo, 1976; Oostendorp, van Oosterom, and Huiskamp, 1992).
In MCG we are interested in the electric activation of the whole cardiac muscle, not only on its anterior surface. Therefore, to compensate the proximity effect, MCG measurements should be done symmetrically both on the anterior and on the posterior side of the thorax. Actually, the posterior measurement of the MCG increases the information especially on the posterior side of the heart, where the sensitivity of all ECG leads is low due to the insulating effect of the lungs. (As noted earlier, in the measurement of the MEG, we are mainly interested in the electric activation of the surface of the brain, the cortex. Therefore a unipolar measurement is more relevant in measuring the MEG.)
On the basis of the existing literature on the MCG, nonsymmetric unipositional measurement seems to give the same diagnostic performance as the mapping of the x component of the magnetic field on the anterior side of the thorax.
A combination of electric and magnetic measurements (i.e., ECG and MCG) gives a better diagnostic performance than either method alone with the same number of diagnostic parameters, because the number of independent measurements doubles.
Baule GM, McFee R (1963): Detection of the magnetic field of the heart. Am. Heart J. 66:(7) 95-6.
Baule GM, McFee R (1970): The magnetic heart vector. Am. Heart J. 79:(2) 223-36.
Cohen D, Chandler L (1969): Measurements and simplified interpretation of magnetocardiograms from humans. Circulation 39: 395-402.
Cohen D, Kaufman LA (1975): Magnetic determination of the relationship between the S-T segment shift and the injury current produced by coronary artery occlusion. Circ. Res. 36: 414.
Cohen D, McCaughan D (1972): Magnetocardiograms and their variation over the chest in normal subjects. Am. J. Cardiol. 29:(5) 678-85.
Cohen D, Norman JC, Molokhia F, Hood W (1971): Magnetocardiography of direct currents: S-T segment and baseline shifts during experimental myocardial infarction. Science 172:(6) 1329-33.
Eskola H (1983): On the properties of vector magnetocardiographic leads. Tampere Univ. Tech., Tampere, Finland, Thesis, pp. 154. (Dr. tech. thesis)
Eskola HJ, Malmivuo JA (1983): Optimizing vector magnetocardiographic lead fields by using physical torso model. Il Nuvo Cim. 2:(2) 356-67.
Gulrajani RM, Savard P, Roberge FA (1988): The inverse problem in electrocardiography: Solution in terms of equivalent sources. CRC Crit. Rev. Biomed. Eng. 16: 171-214.
Karp P (1981): Cardiomagnetism. In Biomagnetism, Proc. Third Internat. Workshop On Biomagnetism, Berlin (West), May 1980, ed. SN Erné, H-D Hahlbohm, H Lübbig, pp. 219-58, Walter de Gruyter, Berlin.
Malmivuo JA (1976): On the detection of the magnetic heart vector - An application of the reciprocity theorem. Helsinki Univ. Tech., Acta Polytechn. Scand., El. Eng. Series. Vol. 39., pp. 112. (Dr. tech. thesis)
Malmivuo JA (1980): Distribution of MEG detector sensitivity: An application of reciprocity. Med. & Biol. Eng. & Comput. 18:(3) 365-70.
Malmivuo JA (1981): Properties of an ideal MCG-recording system. In Biomagnetism. Proc. Third Internat. Workshop On Biomagnetism, Berlin (West), May 1980, ed. SN Erné, H-D Hahlbohm, H Lübbig, pp. 343-9, Walter de Gruyter, Berlin.
Malmivuo JA, Saarinen M, Siltanen P (1973): A clinical method in magnetocardiography. In Digest X Internat. Conf. Med. Biol. Eng, Vol. I, ed. A Albert, W Vogt, W Helbig, p. 251,, Dresden.
Nenonen J, Katila T, Leiniö M, Montonen J, Mäkijärvi M, Siltanen P (1991): Magnetocardiographic functional localization using current multipole models. IEEE Trans. Biomed. Eng. 38:(7) 648-57.
Nenonen J, Purcell CJ, Horácek BM, Stroink G, Katila T (1991): Magnetocardiographic functional localization using a current dipole in a realistic torso. IEEE Trans. Biomed. Eng. 38:(7) 658-64.
Nousiainen JJ (1991): Behavior of the vector magnetocardiogram in normal subjects and in some abnormal cases. Tampere Univ. Tech., Tampere, Finland, Thesis, pp. 177. (Dr. tech. thesis)
Nousiainen JJ, Lekkala JO, Malmivuo JA (1986): Comparative study of the normal vector magnetocardiogram and vector electrocardiogram. J. Electrocardiol. 19:(3) 275-90.
Nousiainen J, Oja S, Malmivuo J (1994a): Normal vector magnetocardiogram. I. Correlation with the normal vector ECG. J. Electrocardiol. 27:(3) 221-231.
Nousiainen J, Oja S, Malmivuo J (1994b): Normal vector magnetocardiogram. II. Effect of constitutional variables. J. Electrocardiol. 27:(3) 233-241.
Oja OS (1993): Vector magnetocardiogram in myocardial disorders. University of Tampere, Medical Faculty, pp. 168. (MD thesis)
Oostendorp TF, van Oosterom A, Huiskamp GJ (1992): The activation sequence of the heart as computed from all three magnetic field components. In Proc. Of the XIX International Congress On Electrocardiology, ., p. 132,, Lisbon.
Rosen A, Inouye GT (1975): A study of the vector magnetocardiographic waveforms. IEEE Trans. Biomed. Eng. BME-22: 167-74.
Rush S (1975): On the interdependence of magnetic and electric body surface recordings. IEEE Trans. Biomed. Eng. BME-22: 157-67.
Saarinen M, Karp P, Katila T, Siltanen P (1978): The normal magnetocardiogram: I. Morphology. Ann. Clin. Res. 10:(S21) 1-43.
Sakauchi Y, Kado H, Awano N, Kasai N, Higuchi M, Chinone K, Nakanishi M, Ohwada K, Kariyone M (1989): Measurement of cardiac magnetic field vector. In Advances in Biomagnetism, ed. SJ Williamson, M Hoke, G Stroink, M Kotani, pp. 425-8, Plenum Press, New York.
Seppänen M, Katila T, Tuomisto T, Varpula T, Duret D, Karp P (1983): Measurement of the biomagnetic fields using multichannel superconducting magnetometer techniques. Il Nuvo Cim. 2 D: 166-74.
Shirae K, Furukawa H, Katayama M (1988): Measurements and characteristics of vector magnetocardiography. In Biomagnetism '87, ed. K Atsumi, M Kotani, S Ueno, T Katila, SJ Williamson, pp. 294-7, Tokyo Denki University Press, Tokyo.
Siltanen P (1989): Magnetocardiography. In Comprehensive Electrocardiology. Theory and Practice in Health and Disease, Vol. 2, ed. PW Macfarlane, TDV Lawrie, pp. 1405-38, Pergamon Press, New York.
Stratton JA (1941): Electromagnetic Theory, McGraw-Hill, New York.
Swithenby SJ (1987): Biomagnetism and the biomagnetic inverse problem. Phys. Med. Biol. MJ Day (ed.): The Biomagnetic Inverse Problem, 32:(1) 146. (Papers from a conference at the Open University, April 1986).
Waller AD (1887): A demonstration on man of electromotive changes accompanying the heart's beat. J. Physiol. (Lond.) 8: 229-34.
Wikswo JP, Malmivuo JA, Barry WM, Leifer M, Fairbank WM (1979): The theory and application of magnetocardiography. In Advances in Cardiovascular Physics, Vol. 2, ed. DN Ghista, pp. 1-67, S. Karger, Basel.
Willems JL, Lesaffre E (1987): Comparison of multigroup logistic and linear discriminant ECG and VCG classification. J. Electrocardiol. 20: 83-92.
 (A) Unipolar (nonsymmetric) measurement location on the anterior side.
(A) Unipolar (nonsymmetric) measurement location on the anterior side.
 (B) Bipolar (symmetric) measurement locations on the anterior and posterior sides.
(B) Bipolar (symmetric) measurement locations on the anterior and posterior sides.20.4.2 Unipolar measurement
As noted before in Section 12.11, in the cylindrically symmetric situation the lead field current is tangentially oriented, and its amplitude is independent of the angle . Therefore, the lead field current distribution may be illustrated as a function of the radial distance r from the symmetry axis, with the distance h from the magnetometer as a parameter. Figure 20.14 illustrates the sensitivity distribution within the region of the spherical heart model for the measurement distance of 100 mm. This is shown both with a series of curves illustrating the lead field current density as a function of radial distance (Figure 20.14A) and with isosensitivity curves (Figure 20.14B). The figure illustrates also the location and size of the magnetometer. This measurement situation corresponds to the measurement of the x component of the MHV with the non-symmetric (unipolar) unipositional lead system on the anterior side of the thorax as illustrated in Figure 20.10. Figure 20.15 illustrates the same information for the measurement distance of 170 mm. This measurement situation corresponds to the unipolar measurement on the posterior side of the thorax.
 As can be seen from Figure 20.14, the sensitivity of the unipolar measurement is concentrated on the anterior region of the heart. This is called the proximity effect.
As can be seen from Figure 20.14, the sensitivity of the unipolar measurement is concentrated on the anterior region of the heart. This is called the proximity effect.
 (A) Sensitivity distribution at the region of the heart. The magnetometer distance h and radial distance r are not shown to the same scale.
(A) Sensitivity distribution at the region of the heart. The magnetometer distance h and radial distance r are not shown to the same scale.
 (B) Isosensitivity curves are illustrated with black dashed lines. Lead field current flow lines are sketched with blue solid lines. The dimensions of h and r are to the same scale.
(B) Isosensitivity curves are illustrated with black dashed lines. Lead field current flow lines are sketched with blue solid lines. The dimensions of h and r are to the same scale.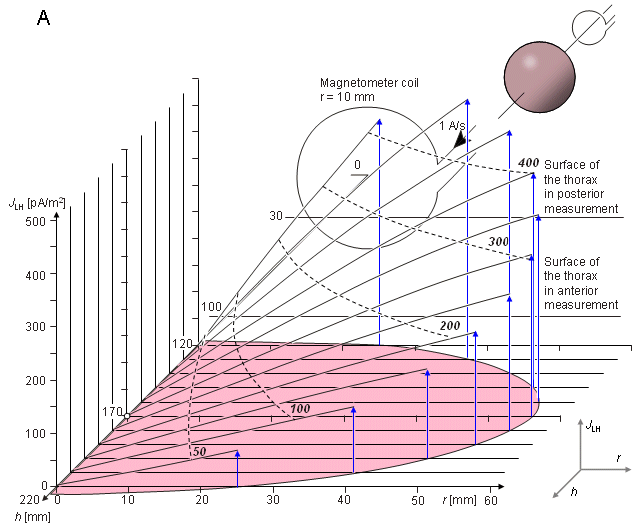
 (A) Sensitivity distribution within the heart region. The magnetometer distance h and radial distance r are not shown in the same scale.
(A) Sensitivity distribution within the heart region. The magnetometer distance h and radial distance r are not shown in the same scale.
 (B) Isosensitivity curves are illustrated with black dashed lines. Lead field current flow lines are sketched with blue solid lines. The dimensions of h and r are in the same scale.
(B) Isosensitivity curves are illustrated with black dashed lines. Lead field current flow lines are sketched with blue solid lines. The dimensions of h and r are in the same scale.20.4.3 Bipolar measurement
The proximity effect can be compensated by using bipolar measurements where the two measurements are made symmetrically on opposite sides of the heart. This is the case in Figures 20.6 and 20.7 in the symmetric (bipolar) XYZ and ABC lead systems, respectively. This is also the case in measuring the x component with the symmetric unipositional lead system as shown in Figure 20.12.
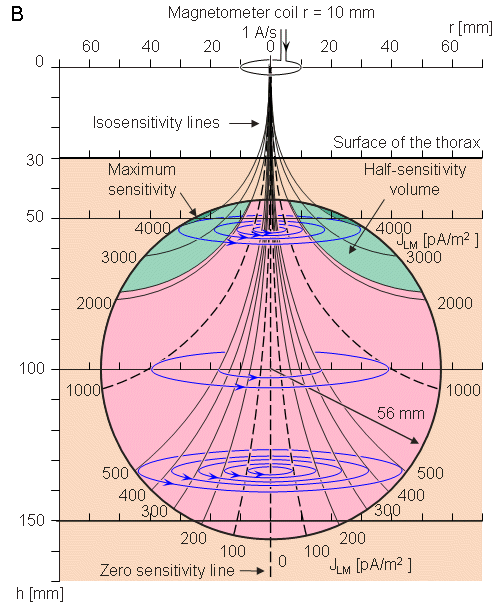
 Figure 20.16 illustrates the sensitivity distribution in the bipolar measurement of the axial component of the magnetic field. The magnetometer coil radius is again 10 mm. The magnetometer distance is on both sides 170 mm from the center of the heart, because this is the minimum distance on the posterior side of the thorax. This measurement situation corresponds to the measurement of the x component of the MHV on both sides of the thorax with the symmetric XYZ lead system or with the symmetric unipositional lead system. (For the symmetric measurement of the y and z components in the XYZ lead system and for all components of the ABC lead system the measurement distances would be larger.) In this figure the lead field current densities of the anterior and posterior measurements are summed. This corresponds to the summing of the corresponding MCG signals. Please note that the noise of these measurements is also summed. Therefore, the sensitivity scales of Figures 20.15 and 20.16 are relevant when comparing signal amplitudes but not when comparing signal-to-noise ratios.
Figure 20.16 illustrates the sensitivity distribution in the bipolar measurement of the axial component of the magnetic field. The magnetometer coil radius is again 10 mm. The magnetometer distance is on both sides 170 mm from the center of the heart, because this is the minimum distance on the posterior side of the thorax. This measurement situation corresponds to the measurement of the x component of the MHV on both sides of the thorax with the symmetric XYZ lead system or with the symmetric unipositional lead system. (For the symmetric measurement of the y and z components in the XYZ lead system and for all components of the ABC lead system the measurement distances would be larger.) In this figure the lead field current densities of the anterior and posterior measurements are summed. This corresponds to the summing of the corresponding MCG signals. Please note that the noise of these measurements is also summed. Therefore, the sensitivity scales of Figures 20.15 and 20.16 are relevant when comparing signal amplitudes but not when comparing signal-to-noise ratios.
 In the measurement of the y and z components of the unipositional lead system the measurement situation is not cylindrically symmetric because the measured fields are not the axial components. Therefore we must assume that the heart model is a conducting sphere surrounded by insulating lung tissue. Figure 20.17 shows the sensitivity distribution in the measurement of the y component. It is shown both in the zx and yz planes. In the measurement of the z component the reciprocal magnetic field is, of course, similar. Note that as discussed in Section 20.3.5, the reciprocal magnetic field strength is one half of that in the measurement of the x component. Therefore the coefficient -2 is needed in Equation 20.7.
In the measurement of the y and z components of the unipositional lead system the measurement situation is not cylindrically symmetric because the measured fields are not the axial components. Therefore we must assume that the heart model is a conducting sphere surrounded by insulating lung tissue. Figure 20.17 shows the sensitivity distribution in the measurement of the y component. It is shown both in the zx and yz planes. In the measurement of the z component the reciprocal magnetic field is, of course, similar. Note that as discussed in Section 20.3.5, the reciprocal magnetic field strength is one half of that in the measurement of the x component. Therefore the coefficient -2 is needed in Equation 20.7.
 Figures 20.16 and 20.17 illustrate that the proximity effect can be very accurately compensated by the bipolar (symmetric) measurement. Because the anterior location of the magnetometer coil is further from the torso surface in the bipolar measurement than in the unipolar, its sensitivity is reduced to that of the posterior magnetometer. Nevertheless the symmetric (bipolar) arrangement is recommended because it yields a sensitivity distribution much closer to the ideal.
Figures 20.16 and 20.17 illustrate that the proximity effect can be very accurately compensated by the bipolar (symmetric) measurement. Because the anterior location of the magnetometer coil is further from the torso surface in the bipolar measurement than in the unipolar, its sensitivity is reduced to that of the posterior magnetometer. Nevertheless the symmetric (bipolar) arrangement is recommended because it yields a sensitivity distribution much closer to the ideal.
 (A) Sensitivity distribution. The region of the heart is shaded. The magnetometer distance h and radial distance r are not shown to the same scale.
(A) Sensitivity distribution. The region of the heart is shaded. The magnetometer distance h and radial distance r are not shown to the same scale.
 (B) Isosensitivity lines are illustrated with black dashed lines. Lead field current flow lines are sketched with blue solid lines. The dimensions of h and r are in scale.
(B) Isosensitivity lines are illustrated with black dashed lines. Lead field current flow lines are sketched with blue solid lines. The dimensions of h and r are in scale.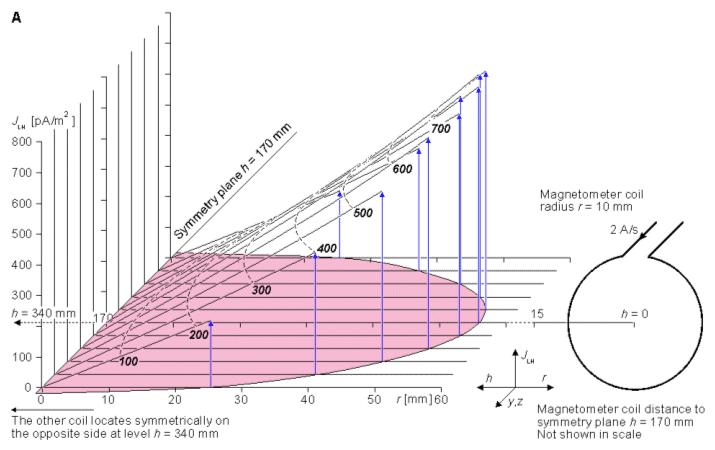
20.5 GENERATION OF THE MCG SIGNAL FROM THE ELECTRIC ACTIVATION OF THE HEART
As pointed out earlier, the source of the MCG signal is the electric activity of the heart muscle. The generation of the MCG signal from the progress of the activation front in the heart can be sketched similarly with the aid of the MCG lead fields, as was done in Section 15.2 for the ECG with the electric lead fields.
 In Figure 20.18 the generation of the MCG signal in the x and z leads is sketched. This illustration is only a rough approximation, and its purpose is to give an impression of the principle of how the signal is produced. As regards the x component, it is assumed that because of the strong proximity effect, the signal is generated mainly from the activation in the anterior part of the heart. As regards the z component, it is pointed out that in nonsymmetric unipositional MCG measurements the zero sensitivity line is located in the posterior side of the heart. Because the sensitivity is proportional to the distance from the zero sensitivity line, the contribution of the anterior part of the heart is again dominating.
In Figure 20.18 the generation of the MCG signal in the x and z leads is sketched. This illustration is only a rough approximation, and its purpose is to give an impression of the principle of how the signal is produced. As regards the x component, it is assumed that because of the strong proximity effect, the signal is generated mainly from the activation in the anterior part of the heart. As regards the z component, it is pointed out that in nonsymmetric unipositional MCG measurements the zero sensitivity line is located in the posterior side of the heart. Because the sensitivity is proportional to the distance from the zero sensitivity line, the contribution of the anterior part of the heart is again dominating.
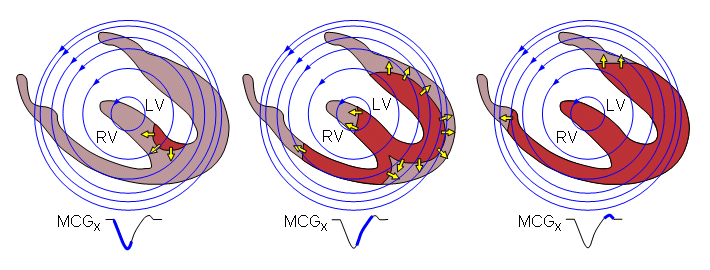
Fig. 20.18 Schematic illustration of the generation of the x component of the MCG signal.
20.6 ECG-MCG RELATIONSHIP
The relationship between the normal ECG and the normal MCG was discussed theoretically in Sections 12.9 and 12.10. In the following, this relationship is examined using actual signal measurements. Figure 20.19 illustrates the averaged electric heart vector of a healthy 30 year old man recorded with the Frank lead system. The averaged magnetic heart vector of the same subject, recorded with the corrected unipositional lead system, is illustrated in Figure 20.20 (Nousiainen, Lekkala, and Malmivuo, 1986; Nousiainen, 1991).
 It may be seen from Figures 20.19 and 20.20 that at the peak of the QRS complex the electric and magnetic heart vectors are very close to being 90° apart. This could also be predicted theoretically (Wikswo et al., 1979). If the angle were always exactly 90°, there would be no new information in the MCG. However, it has been found that this angle varies considerably during the QRS complex, both from patient to patient and in various cardiac disorders. Figure 20.21 shows the variation of this angle as a function of time, and averaged over 17 normal subjects. The arrow indicates the instant of the maximum QRS complex (Nousiainen, Lekkala, and Malmivuo, 1986; Nousiainen, 1991).
It may be seen from Figures 20.19 and 20.20 that at the peak of the QRS complex the electric and magnetic heart vectors are very close to being 90° apart. This could also be predicted theoretically (Wikswo et al., 1979). If the angle were always exactly 90°, there would be no new information in the MCG. However, it has been found that this angle varies considerably during the QRS complex, both from patient to patient and in various cardiac disorders. Figure 20.21 shows the variation of this angle as a function of time, and averaged over 17 normal subjects. The arrow indicates the instant of the maximum QRS complex (Nousiainen, Lekkala, and Malmivuo, 1986; Nousiainen, 1991).
 Not only does the angle between the EHV and the MHV vary during the QRS but their magnitude ratio also varies. Figure 20.22 illustrates this phenomenon. It is possible to identify three peaks - namely M1, M2, and M3 - in the MHV magnitude curve. It was noted in Section 18.3 that M1 appears to be generated by radial, M2 by radial and tangential, and M3 mainly by tangential forces. As pointed out previously, in the ideal case the electric lead is as sensitive to radial as to tangential forces, but the magnetic lead is sensitive only to tangential forces.
Not only does the angle between the EHV and the MHV vary during the QRS but their magnitude ratio also varies. Figure 20.22 illustrates this phenomenon. It is possible to identify three peaks - namely M1, M2, and M3 - in the MHV magnitude curve. It was noted in Section 18.3 that M1 appears to be generated by radial, M2 by radial and tangential, and M3 mainly by tangential forces. As pointed out previously, in the ideal case the electric lead is as sensitive to radial as to tangential forces, but the magnetic lead is sensitive only to tangential forces.
 Figure 20.22 illustrates clearly how the electric measurement, which is more sensitive to the radial electric forces, detects the peak M1 with a relatively higher sensitivity. Peak M3, which is formed mainly by tangential electric forces, is seen in the magnetic measurement as a clearly separate peak. However, at the beginning of this peak the electric signal is larger. The reason for this is not yet clear.
Figure 20.22 illustrates clearly how the electric measurement, which is more sensitive to the radial electric forces, detects the peak M1 with a relatively higher sensitivity. Peak M3, which is formed mainly by tangential electric forces, is seen in the magnetic measurement as a clearly separate peak. However, at the beginning of this peak the electric signal is larger. The reason for this is not yet clear.
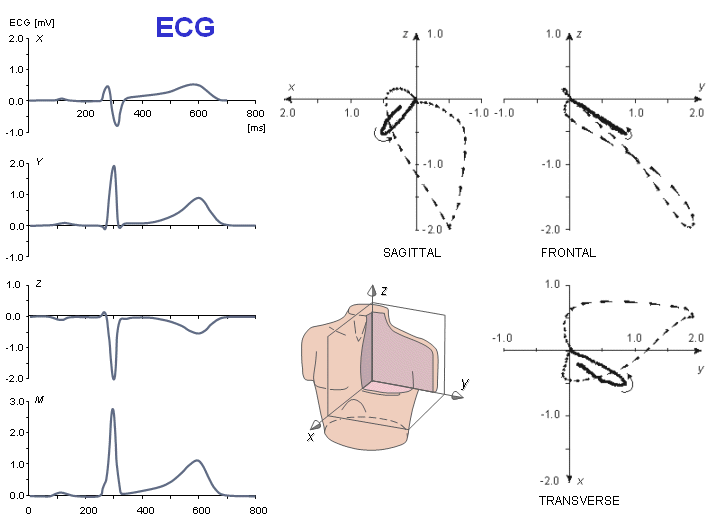
Fig. 20.19 Averaged EHV of a healthy 30 year old man recorded with the Frank lead system.
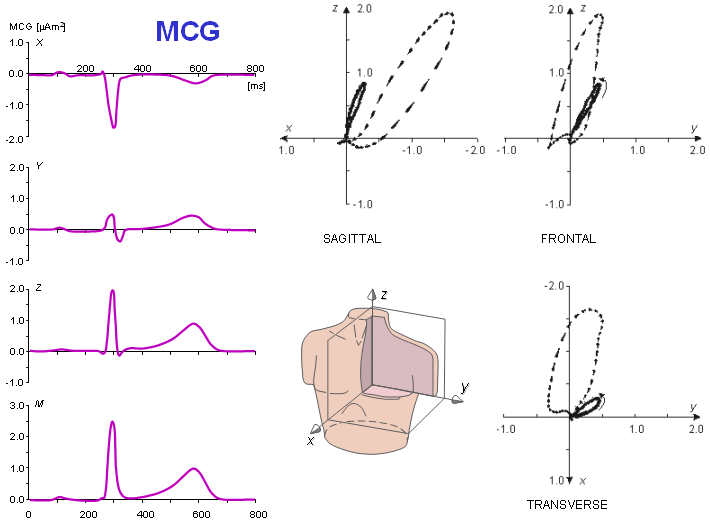
Fig. 20.20 Averaged MHV of the same subject as in the previous figure recorded with the corrected unipositional lead system.
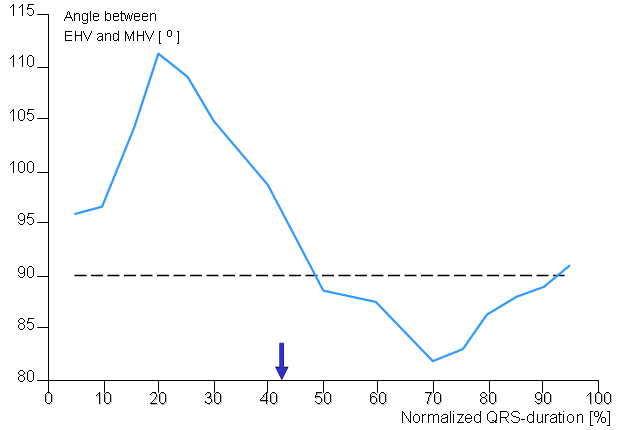
Fig. 20.21 Instantaneous angle between the EHV and the MHV during the normalized duration of the QRS complex. The arrow indicates the maximum value of the MHV. The curve is an average over the QRS complexes of 17 normal subjects.
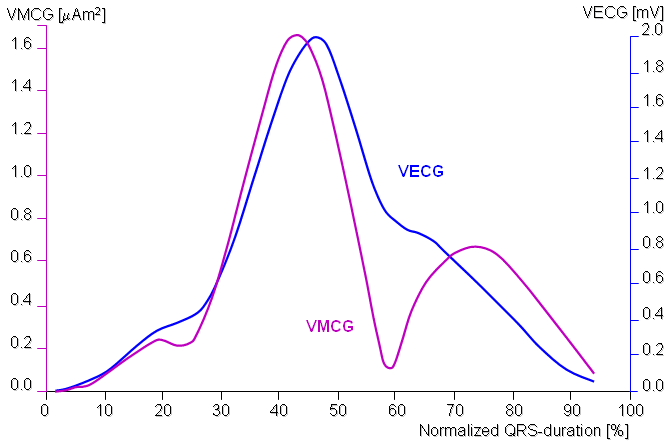
Fig. 20.22 Simultaneous plots of the magnitude curves of the EHV (dashed curve) and the MHV (solid curve) during the QRS complex.
20.7 CLINICAL APPLICATION OF MAGNETOCARDIOGRAPHY
20.7.1 Advantages of magnetocardiography
We have noted that the bioelectric activity in the heart is responsible for the generation of a source current density, namely  i(x,y,z,t). As stated before, both the electric and magnetic fields are generated by this same source which, in turn, responds to the electrophysiological phenomenon of depolarization and repolarization of cardiac muscle cells.
i(x,y,z,t). As stated before, both the electric and magnetic fields are generated by this same source which, in turn, responds to the electrophysiological phenomenon of depolarization and repolarization of cardiac muscle cells.
 A logical question arises as to whether any new information might be provided by the magnetic field measurement that is not available from the electric potential field measurement. While it appears, on certain theoretical grounds, that the electric and magnetic fields are not fully independent, other reasons exist for the use of magnetocardiography. These may be divided into theoretical and technical features. The former ones are based on the universal properties of biomagnetic fields and the latter ones to the technical features of the instrumentation. These are discussed in the following paragraphs.
A logical question arises as to whether any new information might be provided by the magnetic field measurement that is not available from the electric potential field measurement. While it appears, on certain theoretical grounds, that the electric and magnetic fields are not fully independent, other reasons exist for the use of magnetocardiography. These may be divided into theoretical and technical features. The former ones are based on the universal properties of biomagnetic fields and the latter ones to the technical features of the instrumentation. These are discussed in the following paragraphs.
Theoretical advantages
First, the nature of lead fields of electric and magnetic leads is quite different, as described in Section 12.9. Specifically, the ideal magnetic lead is sensitive only to tangential components of activation sources and therefore should be particularly responsive to abnormalities in activation (since normal activation sources are primarily radial). Furthermore, the tangential components are attenuated in the ECG because of the Brody effect. Another factor is that the signal-to-noise ratio for the electrical and magnetic recordings are affected by different factors, so there could be a practical advantage in using one over the other despite their similarities in content.
 Second, the magnetic permeability of the tissue is that of free space. Therefore the sensitivity of the MCG is not affected by the high electric resistivity of lung tissue. This makes it possible to record with MCG from the posterior side of the thorax the electric activity of the posterior side of the heart. That is difficult to do with surface ECG electrodes, but is possible to do with an esophageal electrode which is, however, inconvenient for the patient. Another important application of this feature is the recording of the fetal MCG. During certain phase of pregnancy the fetal ECG is very difficult to record because of the insulating fat layer in the fetus.
Second, the magnetic permeability of the tissue is that of free space. Therefore the sensitivity of the MCG is not affected by the high electric resistivity of lung tissue. This makes it possible to record with MCG from the posterior side of the thorax the electric activity of the posterior side of the heart. That is difficult to do with surface ECG electrodes, but is possible to do with an esophageal electrode which is, however, inconvenient for the patient. Another important application of this feature is the recording of the fetal MCG. During certain phase of pregnancy the fetal ECG is very difficult to record because of the insulating fat layer in the fetus.
Technical advantages
First, a possibly important distinction is that the magnetic detector is not in contact with the subject. For mass screening, there is an advantage in not requiring skin preparation and attachment of electrodes. (In the case of patients with skin burns this is a crucial advantage.)
 Second, the SQUID (Superconducting QUantum Interference Device) magnetometer is readily capable of measuring DC signals. These are associated with the S-T segment shift in myocardial infarction (Cohen et al., 1971; Cohen and Kaufman, 1975). Such signals can be obtained electrically only with great difficulty. Although the clinical value has yet to be demonstrated, it should be noted that because of the difficulty in performing electrical measurements, there have been few investigations of DC potentials.
Second, the SQUID (Superconducting QUantum Interference Device) magnetometer is readily capable of measuring DC signals. These are associated with the S-T segment shift in myocardial infarction (Cohen et al., 1971; Cohen and Kaufman, 1975). Such signals can be obtained electrically only with great difficulty. Although the clinical value has yet to be demonstrated, it should be noted that because of the difficulty in performing electrical measurements, there have been few investigations of DC potentials.
20.7.2 Disadvantages of magnetocardiography
There are many reasons for preferring the use of the ECG rather than the MCG. An important consideration is the ease of application. For example, if only the heart rate is desired, then the ECG may prove much simpler. The reason is that the measurement of the MCG, at present, is technologically more complicated and requires complex and expensive equipment. Specifically, this includes a SQUID magnetometer, liquid helium, and a low-noise environment. Because of the development of the SQUID technology, a shielded room is no longer needed in magnetocardiography. (In the near future, it seems possible to operate the SQUIDs at the liquid nitrogen temperature which decreases the operational costs considerably.)
20.7.3 Clinical application
The clinical application of magnetocardiography may be based on either theoretical (bioelectromagnetic) or technical features of the method. The main technical benefits of MCG are given in Section 20.2.1. The theoretical features include the different sensitivity distribution of the MCG to the bioelectric sources of the heart.
 Several studies on the diagnostic performance of the MCG have been published in the literature. An overview of these can be found in the review article of Siltanen (1989). The patient materials have included most of the main categories of cardiac diseases that are investigated with ECG, including infarction, hypertrophy, and conduction defects. In most studies the MCG has been done with the mapping method by recording only the x component of the heart's magnetic field at several recording points on the anterior side of the thorax without utilizing the vectorial nature of the magnetic field (Cohen and McCaughan, 1972; Saarinen et al., 1978). There are also many reports in which the three components of the magnetic vector field of the heart have been recorded with the mapping method (Cohen and Chandler, 1969; Rosen and Inouye, 1975; Seppänen et al., 1983; Shirae, Furukawa, and Katayama, 1988; Sakauchi et al., 1989). In the mapping method, the number of the measurement points is usually 30-40. If the signal is recorded with a single-channel magnetometer (as is usually done because of the large dimensions of the measurement grid) and if we assume 1 minute for positioning the magnetometer and another minute for data collection, this leads to a total recording time of more than 1 hour per patient. Using the mapping method for various cardiac abnormalities, the diagnostic performance of the MCG has been, on average, about the same as that of the ECG.
Several studies on the diagnostic performance of the MCG have been published in the literature. An overview of these can be found in the review article of Siltanen (1989). The patient materials have included most of the main categories of cardiac diseases that are investigated with ECG, including infarction, hypertrophy, and conduction defects. In most studies the MCG has been done with the mapping method by recording only the x component of the heart's magnetic field at several recording points on the anterior side of the thorax without utilizing the vectorial nature of the magnetic field (Cohen and McCaughan, 1972; Saarinen et al., 1978). There are also many reports in which the three components of the magnetic vector field of the heart have been recorded with the mapping method (Cohen and Chandler, 1969; Rosen and Inouye, 1975; Seppänen et al., 1983; Shirae, Furukawa, and Katayama, 1988; Sakauchi et al., 1989). In the mapping method, the number of the measurement points is usually 30-40. If the signal is recorded with a single-channel magnetometer (as is usually done because of the large dimensions of the measurement grid) and if we assume 1 minute for positioning the magnetometer and another minute for data collection, this leads to a total recording time of more than 1 hour per patient. Using the mapping method for various cardiac abnormalities, the diagnostic performance of the MCG has been, on average, about the same as that of the ECG.
 We briefly summarize here the results of one study, made at the Ragnar Granit Institute in cooperation with the Tampere University Hospital, where the diagnostic performance of magnetocardiography was studied utilizing the unipositional lead system (Oja, 1993). A total of 526 subjects were chosen, of whom 290 were healthy subjects and 236 patients had various cardiac disorders including myocardial infarction, left ventricular hypertrophy, ventricular conduction defects, and Wolf-Parkinson-White syndrome. The statistical analysis to evaluate the diagnostic performance of VECG (Frank lead system) and VMCG was made with a stepwise linear discriminant analysis.
We briefly summarize here the results of one study, made at the Ragnar Granit Institute in cooperation with the Tampere University Hospital, where the diagnostic performance of magnetocardiography was studied utilizing the unipositional lead system (Oja, 1993). A total of 526 subjects were chosen, of whom 290 were healthy subjects and 236 patients had various cardiac disorders including myocardial infarction, left ventricular hypertrophy, ventricular conduction defects, and Wolf-Parkinson-White syndrome. The statistical analysis to evaluate the diagnostic performance of VECG (Frank lead system) and VMCG was made with a stepwise linear discriminant analysis.
 The variation of the VMCG in normal subjects and the effect of constitutional variables were first investigated by Nousiainen and colleagues (Nousiainen, 1991; Nousiainen, Oja, and Malmivuo, 1994ab). This forms the basis for determining the diagnostic performance of the VMCG.
The variation of the VMCG in normal subjects and the effect of constitutional variables were first investigated by Nousiainen and colleagues (Nousiainen, 1991; Nousiainen, Oja, and Malmivuo, 1994ab). This forms the basis for determining the diagnostic performance of the VMCG.
 The diagnostic performance of the VECG and the VMCG were first compared in their capacity to distinguish among five groups consisting of (1) normal subjects; and patients with (2) anteroseptal myocardial infarction, (3) inferior myocardial infarction, (4) lateral myocardial infarction, and (5) left ventricular hypertrophy. When the VECG was used, the best results were obtained when a total of 30 parameters from the QRS vector and ST-T segment were used. In the VMCG, the best results were obtained by using 11 parameters from the QRS vector and two from the ST-T segment. Under these conditions the sensitivity (i.e., percentage classified correctly) of the VECG and VMCG were the same, namely 73.7%.
The diagnostic performance of the VECG and the VMCG were first compared in their capacity to distinguish among five groups consisting of (1) normal subjects; and patients with (2) anteroseptal myocardial infarction, (3) inferior myocardial infarction, (4) lateral myocardial infarction, and (5) left ventricular hypertrophy. When the VECG was used, the best results were obtained when a total of 30 parameters from the QRS vector and ST-T segment were used. In the VMCG, the best results were obtained by using 11 parameters from the QRS vector and two from the ST-T segment. Under these conditions the sensitivity (i.e., percentage classified correctly) of the VECG and VMCG were the same, namely 73.7%.
 Significant improvements in the classification rate in classifying the five aforementioned groups were obtained, when part of the 30 parameters were selected from the ECG and the rest from the MCG. In this combination of ECG and MCG the correct classification rate was 81.4%. The improvement in the diagnostic performance is based on the fact that the MCG leads are independent of the ECG leads. Therefore, though both ECG and MCG have about the same diagnostic performance and the number of the correctly diagnosed patients is about the same, these groups are not identical. In the combination of ECG and MCG, called electromagnetocardiogram (EMCG), it is possible to combine the groups of the correctly diagnosed patients, as illustrated in Figure 20.23.
Significant improvements in the classification rate in classifying the five aforementioned groups were obtained, when part of the 30 parameters were selected from the ECG and the rest from the MCG. In this combination of ECG and MCG the correct classification rate was 81.4%. The improvement in the diagnostic performance is based on the fact that the MCG leads are independent of the ECG leads. Therefore, though both ECG and MCG have about the same diagnostic performance and the number of the correctly diagnosed patients is about the same, these groups are not identical. In the combination of ECG and MCG, called electromagnetocardiogram (EMCG), it is possible to combine the groups of the correctly diagnosed patients, as illustrated in Figure 20.23.
 On the basis of this study and the existing literature of other studies, we may draw the following conclusions concerning the diagnostic performance of MCG:
On the basis of this study and the existing literature of other studies, we may draw the following conclusions concerning the diagnostic performance of MCG:
20.7.4 Basis for the increase in diagnostic performance by biomagnetic measurement
The basic idea behind the increase in diagnostic performance when applying electromagnetocardiography (item 4. above) is fundamental to the application of biomagnetic methods to clinical diagnosis in general and it may be further clarified as follows.
 If the MCG leads were a linear combination of the ECG leads (as is the case in Figure 20.3), the groups of correctly diagnosed patients would be identical in both tests. Such a case has been demonstrated by Willems and Lesaffre (1987) who have shown that the 12-lead ECG and Frank VCG have an equal diagnostic performance. A combination of these lead systems did not improve the diagnostic performance. That is natural, however, because one of these lead systems is a linear combination of the other one.
If the MCG leads were a linear combination of the ECG leads (as is the case in Figure 20.3), the groups of correctly diagnosed patients would be identical in both tests. Such a case has been demonstrated by Willems and Lesaffre (1987) who have shown that the 12-lead ECG and Frank VCG have an equal diagnostic performance. A combination of these lead systems did not improve the diagnostic performance. That is natural, however, because one of these lead systems is a linear combination of the other one.
 But, as the Helmholtz theorem states, the ECG and MCG leads are mathematically independent. Therefore the correctly diagnosed patient materials with both methods are about as large, but not identical. Therefore with a combination of the ECG and MCG signals it is possible to combine the groups of correctly diagnosed patients and to increase the diagnostic performance even without increasing the number of parameters in the diagnostic procedure. This is a consequence of the fact that in the combined method we have 3 + 3 = 6 independent leads if both ECG and MCG are based on the dipole model.
But, as the Helmholtz theorem states, the ECG and MCG leads are mathematically independent. Therefore the correctly diagnosed patient materials with both methods are about as large, but not identical. Therefore with a combination of the ECG and MCG signals it is possible to combine the groups of correctly diagnosed patients and to increase the diagnostic performance even without increasing the number of parameters in the diagnostic procedure. This is a consequence of the fact that in the combined method we have 3 + 3 = 6 independent leads if both ECG and MCG are based on the dipole model.
 This principle is illustrated in Figure 20.23, where the whole population is represented with a large circle. Suppose that the patients who are diagnosed correctly with ECG can be represented with a smaller circle within it, and those patients who can be diagnosed correctly with MCG can be represented with another similar circle. If the ECG and MCG systems include the same number of independent measurements (both are, for instance, based on a dipole model), their diagnostic performances are about as good and thus the areas of the circles representing the number of correctly diagnosed patients with each system have about an equal area.
This principle is illustrated in Figure 20.23, where the whole population is represented with a large circle. Suppose that the patients who are diagnosed correctly with ECG can be represented with a smaller circle within it, and those patients who can be diagnosed correctly with MCG can be represented with another similar circle. If the ECG and MCG systems include the same number of independent measurements (both are, for instance, based on a dipole model), their diagnostic performances are about as good and thus the areas of the circles representing the number of correctly diagnosed patients with each system have about an equal area.
 Because we do not know which are the individual patients who are diagnosed correctly with ECG but incorrectly with MCG, or vice versa, with separate diagnostic systems of ECG and MCG we cannot increase the overall diagnostic performance. (If we could know who are the patients who are diagnosed correctly and who are diagnosed incorrectly, then the diagnostic performance would, of course, be 100%!) The overall diagnostic performance can be increased only if both the electric and the magnetic signals are simultaneously included in the diagnostic procedure in the form of electromagnetocardiography (EMCG). The diagnostic performance of the combined system would then equal the surface bordered together by the ECG and MCG circles lying slightly apart.
Because we do not know which are the individual patients who are diagnosed correctly with ECG but incorrectly with MCG, or vice versa, with separate diagnostic systems of ECG and MCG we cannot increase the overall diagnostic performance. (If we could know who are the patients who are diagnosed correctly and who are diagnosed incorrectly, then the diagnostic performance would, of course, be 100%!) The overall diagnostic performance can be increased only if both the electric and the magnetic signals are simultaneously included in the diagnostic procedure in the form of electromagnetocardiography (EMCG). The diagnostic performance of the combined system would then equal the surface bordered together by the ECG and MCG circles lying slightly apart.
 This is the fundamental principle behind the increase of diagnostic performance which can be achieved with a biomagnetic method in addition to that of a bioelectric method. This principle is not only applicable to magnetocardiography but may also be applied to magnetoencephalography and other areas of biomagnetism as well.
This is the fundamental principle behind the increase of diagnostic performance which can be achieved with a biomagnetic method in addition to that of a bioelectric method. This principle is not only applicable to magnetocardiography but may also be applied to magnetoencephalography and other areas of biomagnetism as well.

 (A) If electric and magnetic methods (ECG and MCG) are based on source models having the same number of independent variables, the number of correctly diagnosed patients is about the same with both methods. The more different the sensitivity distributions of these systems, the more clearly differentiated are the populations of correctly diagnosed patients. Because we do not know which individual patients are diagnosed correctly with each method, the overall diagnostic performance cannot be increased by use of separate electric and magnetic methods.
(A) If electric and magnetic methods (ECG and MCG) are based on source models having the same number of independent variables, the number of correctly diagnosed patients is about the same with both methods. The more different the sensitivity distributions of these systems, the more clearly differentiated are the populations of correctly diagnosed patients. Because we do not know which individual patients are diagnosed correctly with each method, the overall diagnostic performance cannot be increased by use of separate electric and magnetic methods.
 (B) If the diagnosis is based on the combination of electric and magnetic data (EMCG), the number of correctly diagnosed patients may be increased to the area bordered with correctly diagnosed patients by both methods.
(B) If the diagnosis is based on the combination of electric and magnetic data (EMCG), the number of correctly diagnosed patients may be increased to the area bordered with correctly diagnosed patients by both methods.20.7.5 General conclusions on magnetocardiography
On the basis of the theory of bioelectromagnetism and the existing literature on MCG research, we may draw the following general conclusions regarding the application of magnetocardiography (Malmivuo, 1976):
REFERENCES



