22.1 INTRODUCTION
In Chapter 12 it was pointed out that the origin of the biomagnetic field is the electric activity of biological tissue. This bioelectric activity produces an electric current in the volume conductor which induces the biomagnetic field. This correlation between the bioelectric and biomagnetic phenomena is, of course, not limited to the generation of the bioelectric and biomagnetic fields by the same bioelectric sources. This correlation also arises in the stimulation of biological tissue. Magnetic stimulation is a method for stimulating excitable tissue with an electric current induced by an external time-varying magnetic field. It is important to note here that, as in the electric and magnetic detection of the bioelectric activity of excitable tissues, both the electric and the magnetic stimulation methods excite the membrane with electric current. The former does that directly, but the latter does it with the electric current which is induced within the volume conductor by the time-varying applied magnetic field.
Magnetic stimulation is a method for stimulating excitable tissue with an electric current induced by an external time-varying magnetic field. It is important to note here that, as in the electric and magnetic detection of the bioelectric activity of excitable tissues, both the electric and the magnetic stimulation methods excite the membrane with electric current. The former does that directly, but the latter does it with the electric current which is induced within the volume conductor by the time-varying applied magnetic field.
 The reason for using a time-varying magnetic field to induce the stimulating current is, on the one hand, the different distribution of stimulating current and, on the other hand, the fact that the magnetic field penetrates unattenuated through such regions as the electrically insulating skull. This makes it possible to avoid a high density of stimulating current at the scalp in stimulating the central nervous system and thus avoid pain sensation. Also, no physical contact of the stimulating coil and the target tissue is required, unlike with electric stimulation.
The reason for using a time-varying magnetic field to induce the stimulating current is, on the one hand, the different distribution of stimulating current and, on the other hand, the fact that the magnetic field penetrates unattenuated through such regions as the electrically insulating skull. This makes it possible to avoid a high density of stimulating current at the scalp in stimulating the central nervous system and thus avoid pain sensation. Also, no physical contact of the stimulating coil and the target tissue is required, unlike with electric stimulation.
 The first documents on magnetic stimulation described the stimulation of the retina by Jacques d'Arsonval (1896) and Silvanus P. Thompson (1910). The retina is known to be very sensitive to stimulation by induced currents, and field strengths as low as 10 mT rms at 20 Hz will cause a stimulation (Lövsund, Öberg, and Nilsson, 1980).
The first documents on magnetic stimulation described the stimulation of the retina by Jacques d'Arsonval (1896) and Silvanus P. Thompson (1910). The retina is known to be very sensitive to stimulation by induced currents, and field strengths as low as 10 mT rms at 20 Hz will cause a stimulation (Lövsund, Öberg, and Nilsson, 1980).
 From the pioneering works of d'Arsonval and Thompson it took some time before the magnetic method was applied to neuromuscular stimulation. Bickford and Fremming (1965) used a damped 500 Hz sinusoidal magnetic field and demonstrated muscular stimulation in animals and humans. Magnetic stimulation of nerve tissue was also demonstrated by Öberg (1973). The first successful magnetic stimulation of superficial nerves was reported by Polson et al. in 1982 (Polson, Barker, and Freeston, 1982).
From the pioneering works of d'Arsonval and Thompson it took some time before the magnetic method was applied to neuromuscular stimulation. Bickford and Fremming (1965) used a damped 500 Hz sinusoidal magnetic field and demonstrated muscular stimulation in animals and humans. Magnetic stimulation of nerve tissue was also demonstrated by Öberg (1973). The first successful magnetic stimulation of superficial nerves was reported by Polson et al. in 1982 (Polson, Barker, and Freeston, 1982).
 Transcranial stimulation of the motor cortex is the most interesting application of magnetic stimulation because the magnetic field (unlike the electric current) penetrates through the skull without attenuation. The first transcranial stimulation of the central nervous system was achieved in 1985 (Barker and Freeston, 1985; Barker, Freeston, Jalinous, Merton, and Morton, 1985; Barker, Jalinous, and Freeston, 1985). A more complete history of magnetic stimulation may be found from a review article of Geddes (1991).
Transcranial stimulation of the motor cortex is the most interesting application of magnetic stimulation because the magnetic field (unlike the electric current) penetrates through the skull without attenuation. The first transcranial stimulation of the central nervous system was achieved in 1985 (Barker and Freeston, 1985; Barker, Freeston, Jalinous, Merton, and Morton, 1985; Barker, Jalinous, and Freeston, 1985). A more complete history of magnetic stimulation may be found from a review article of Geddes (1991).
22.2 THE DESIGN OF STIMULATOR COILS
A magnetic stimulator includes a coil that is placed on the surface of the skin. To induce a current into the underlying tissue, a strong and rapidly changing magnetic field must be generated by the coil. In practice, this is generated by first charging a large capacitor to a high voltage and then discharging it with a thyristor switch through a coil. The principle of a magnetic stimulator is illustrated in Figure 22.1. The Faraday-Henry law states that if an electric conductor, which forms a closed circuit, is linked by a time-varying magnetic flux F, a current is observed in the circuit. This current is due to the electromotive force (emf) induced by the time-varying flux. The magnitude of emf depends on the rate of change of the magnetic flux dF/dt. The direction of emf is such that the time-varying magnetic field that results from it is always opposite to that of dF/dt; therefore,
The Faraday-Henry law states that if an electric conductor, which forms a closed circuit, is linked by a time-varying magnetic flux F, a current is observed in the circuit. This current is due to the electromotive force (emf) induced by the time-varying flux. The magnitude of emf depends on the rate of change of the magnetic flux dF/dt. The direction of emf is such that the time-varying magnetic field that results from it is always opposite to that of dF/dt; therefore,
 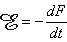 | (22.1) |
| where | 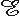 | = electromotive force (emf) [V] |
| F | = magnetic flux [Wb = Vs] | |
| t | = time [s] |
Corresponding to a magnetic field  the flux
the flux 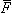 , linking the circuit is given by
, linking the circuit is given by 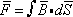 , where the integral is taken over any surface whose periphery is the circuit loop.
, where the integral is taken over any surface whose periphery is the circuit loop.
 If the flux is due to a coil's own current I, the flux is defined as: F = LI, where L is the inductance of the coil and the emf can be written
If the flux is due to a coil's own current I, the flux is defined as: F = LI, where L is the inductance of the coil and the emf can be written
 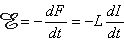 | (22.2) |
| where | L | = inductance of the coil [H =Wb/A = Vs/A] |
| I | = current in the coil [A] |
and other variables are as in Equation 22.1.
 The magnitude of induced emf is proportional to the rate of change of current, dI/dt. The coefficient of proportionality is the inductance L. The term dI/dt depends on the speed with which the capacitors are discharged; the latter is increased by use of a fast solid-state switch (i.e., fast thyristor) and minimal wiring length. Inductance L is determined by the geometry and constitutive property of the medium. The principal factors for the coil system are the shape of the coil, the number of turns on the coil, and the permeability of the core. For typical coils used in physiological magnetic stimulation, the inductance may be calculated from the following equations:
The magnitude of induced emf is proportional to the rate of change of current, dI/dt. The coefficient of proportionality is the inductance L. The term dI/dt depends on the speed with which the capacitors are discharged; the latter is increased by use of a fast solid-state switch (i.e., fast thyristor) and minimal wiring length. Inductance L is determined by the geometry and constitutive property of the medium. The principal factors for the coil system are the shape of the coil, the number of turns on the coil, and the permeability of the core. For typical coils used in physiological magnetic stimulation, the inductance may be calculated from the following equations:
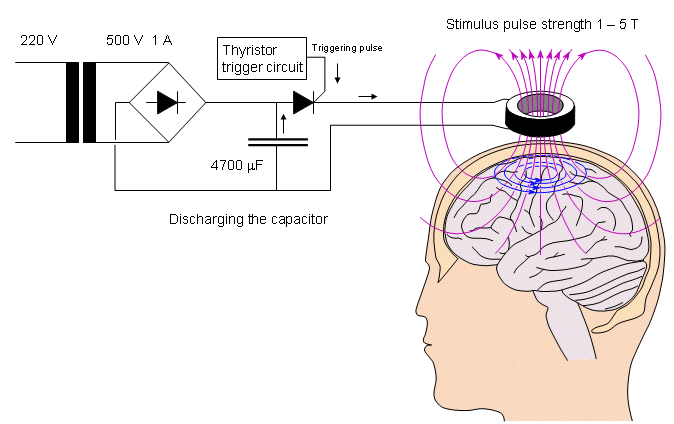
- Fig. 22.1 The principle of the magnetic stimulator.
Multiple-Layer Cylinder Coil
The inductance of a multiple-layer cylinder coil (Figure 22.2A) is:
 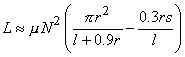 | (22.3) |
| where | L | = inductance of the coil [H] |
| µ | = permeability of the coil core [Vs/Am] | |
| N | = number of turns on the coil | |
| r | = coil radius [m] | |
| l | = coil length [m] | |
| s | = coil width [m] |
 The following example is given of the electric parameters of a multiple-layer cylinder coil (Rossi et al., 1987): A coil having 19 turns of 2.5 mm² copper wound in three layers has physical dimensions of r = 18 mm, l = 22 mm, and s = 6 mm. The resistance and the inductance of the coil were measured to be 14 mΩ and 169 µH, respectively.
The following example is given of the electric parameters of a multiple-layer cylinder coil (Rossi et al., 1987): A coil having 19 turns of 2.5 mm² copper wound in three layers has physical dimensions of r = 18 mm, l = 22 mm, and s = 6 mm. The resistance and the inductance of the coil were measured to be 14 mΩ and 169 µH, respectively.
Flat Multiple-Layer Disk Coil
The inductance of a flat multiple-layer disk coil (Figure 22.2B) is
 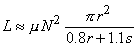 | (22.4) |
where N, r, and s are the same as in the equation above.
 A coil having 10 turns of 2.5 mm² copper wire in one layer has physical dimensions of r = 14 ... 36 mm. The resistance and the inductance of the coil had the measured values of 10 mΩ and 9.67 µH, respectively.
A coil having 10 turns of 2.5 mm² copper wire in one layer has physical dimensions of r = 14 ... 36 mm. The resistance and the inductance of the coil had the measured values of 10 mΩ and 9.67 µH, respectively.
Long Single-Layer Cylinder Coil
The inductance of a long single-layer cylinder coil (Figure 22.2C) is
 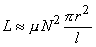 | (22.5) |
where N, r, and l are again the same as in the equation above.
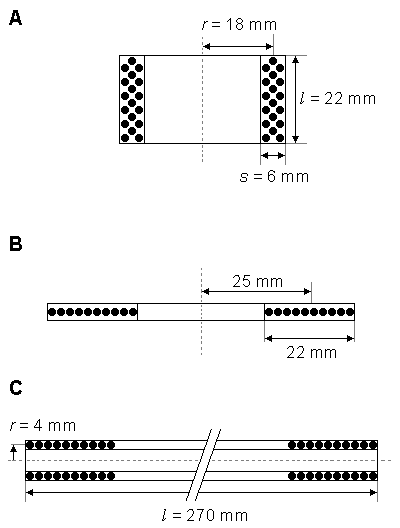
- Fig. 22.2 Dimensions of coils of different configuration:
 A) Multiple-layer cylinder coil.
A) Multiple-layer cylinder coil.
 B) Flat multiple-layer disk coil.
B) Flat multiple-layer disk coil.
 C) Long single-layer cylinder coil.
C) Long single-layer cylinder coil.Expressions for inductance of these coils are given in Equations 22.3 - 22.5.
22.3 CURRENT DISTRIBUTION IN MAGNETIC STIMULATION
The magnetic permeability of biological tissue is approximately that of a vacuum. Therefore the tissue does not have any noticeable effect on the magnetic field itself. The rapidly changing field of the magnetic impulse induces electric current in the tissue, which produces the stimulation. Owing to the reciprocity theorem, the current density distribution of a magnetic stimulator is the same as the sensitivity distribution of such a magnetic detector having a similar construction. (Similarly, this is, of course, true for electric stimulators and detectors as well (Malmivuo, 1992a,b).) Note that in the lead field theory, the reciprocal energization equals the application of stimulating energy. The distribution of the current density in magnetic stimulation may be calculated using the method introduced by Malmivuo (1976) and later applied for the MEG (Malmivuo, 1980). As mentioned in Section 14.3, there are also other methods for calculating the sensitivity distribution of MEG detectors. They give accurate results in situations having less symmetry and are therefore more complicated and, unfortunately, less illustrative (Durand, Ferguson, and Dalbasti, 1992; Eaton, 1992; Esselle and Stuchly, 1992).
Owing to the reciprocity theorem, the current density distribution of a magnetic stimulator is the same as the sensitivity distribution of such a magnetic detector having a similar construction. (Similarly, this is, of course, true for electric stimulators and detectors as well (Malmivuo, 1992a,b).) Note that in the lead field theory, the reciprocal energization equals the application of stimulating energy. The distribution of the current density in magnetic stimulation may be calculated using the method introduced by Malmivuo (1976) and later applied for the MEG (Malmivuo, 1980). As mentioned in Section 14.3, there are also other methods for calculating the sensitivity distribution of MEG detectors. They give accurate results in situations having less symmetry and are therefore more complicated and, unfortunately, less illustrative (Durand, Ferguson, and Dalbasti, 1992; Eaton, 1992; Esselle and Stuchly, 1992).
Single Coil
The current distribution of a single coil, producing a dipolar field, was presented earlier in this book in Sections 12.11 and 14.2. The stimulation energy distribution can be readily seen in the form of vector fields from Figure 14.2 and is not repeated here. Figure 22.3 illustrates the iso-intensity lines and half-intensity volume for a coil with a 50 mm radius. The concepts of iso-intensity line and half-intensity volume are reciprocal to the isosensitivity line and half-sensitivity volume, discussed in Section 11.6.1. As discussed in Section 12.3.3, because of cylindrical symmetry the iso-intensity lines coincide with the magnetic field lines. The reader may again compare the effect of the coil radius on the distribution of the stimulus current by comparing Figures 22.3 and 14.3..
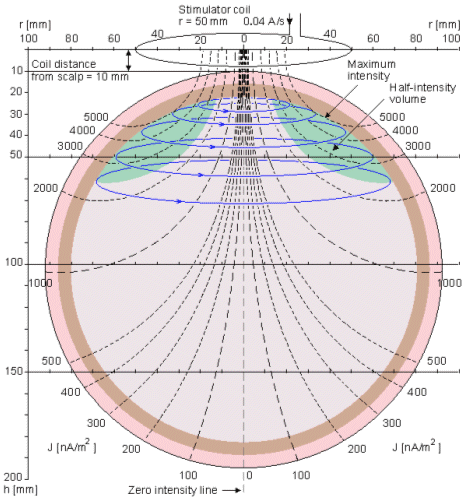
Fig. 22.3 Iso-intensity lines (dashed black), induced stimulation currrent lines (solid blue) and half-intensity volume (green) for a stimulation coil with 50 mm radius. The distance of the coil plane from the scalp is 10 mm.
Quadrupolar Coil Configuration
The coils can be equipped with cores of highly permeable material. One advantage of this arrangement is that the magnetic field that is produced is better focused in the desired location. Constructing the permeable core in the form of the letter U results in the establishment of a quadrupolar magnetic field source. With a quadrupolar magnetic field the stimulating electric current field in the tissue has a linear instead of circular form. In some applications the result is more effective stimulation. On the other hand, a quadrupolar field decreases as a function of distance faster than that of a dipolar coil. Therefore, the dipolar coil is more effective in stimulating objects that are located deeper within the tissue. The first experiments with the quadrupolar magnetic field were made by Rossi et al. (1987). The distribution of the stimulating electric current field of a figure of eight coil system was calculated by Malmivuo (1987). This method has subsequently been applied to magnetic stimulation by many scientists (Ueno, Tashiro, and Harada, 1988).
The first experiments with the quadrupolar magnetic field were made by Rossi et al. (1987). The distribution of the stimulating electric current field of a figure of eight coil system was calculated by Malmivuo (1987). This method has subsequently been applied to magnetic stimulation by many scientists (Ueno, Tashiro, and Harada, 1988).
 The sensitivity distributions of dipolar and quadrupolar magnetometer coils were discussed in detail in Section 14.2. The sensitivity distributions shown in Figures 14.4 and 14.5 are similarly applicable to magnetic stimulation as well and are therefore not reproduced here.
The sensitivity distributions of dipolar and quadrupolar magnetometer coils were discussed in detail in Section 14.2. The sensitivity distributions shown in Figures 14.4 and 14.5 are similarly applicable to magnetic stimulation as well and are therefore not reproduced here.
22.4 STIMULUS PULSE
The experimental stimulator examined by Irwin et al. (1970) had a multicapacitor construction equaling a capacitance of 4760 µF. This was charged to 90-260 V and then discharged with a bank of eight thyristors through the stimulating coil. The result was a magnetic field pulse of 0.1-0.2 T, 5 mm away from the coil. The length of the magnetic field pulse was of the order of 150-300 µs. Today's commercial magnetic stimulators generate magnetic energies of some 500 J and use typically 3 ... 5 kV to drive the coil. Peak fields are typically 2 T, risetimes of order 100 µs, and peak values of dB/dt = 5×104 T/s. The energy required to stimulate tissue is proportional to the square of the corresponding magnetic field. According to Faraday's induction law, this magnetic field is in turn approximately proportional to the product of the electric field magnitude and the pulse duration (Irwin et al., 1970):
The energy required to stimulate tissue is proportional to the square of the corresponding magnetic field. According to Faraday's induction law, this magnetic field is in turn approximately proportional to the product of the electric field magnitude and the pulse duration (Irwin et al., 1970):
 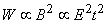 | (22.6) |
Thus
 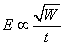 | (22.7) |
| where | W | = energy required to stimulate tissue |
| B | = magnetic flux density | |
| E | = electric field | |
| t | = pulse duration |
 The effectiveness of the stimulator with respect to energy transfer is proportional to the square root of the magnetic energy stored in the coil when the current in the coil reaches its maximum value. A simple model of a nerve fiber is to regard each node as a leaky capacitor that has to be charged. Measurements with electrical stimulation indicate that the time constant of this leaky capacitor is of the order of 150-300 µs. Therefore, for effective stimulation the current pulse into the node should be shorter than this (Hess, Mills, and Murray, 1987). For a short pulse in the coil less energy is required, but obviously there is a lower limit too.
The effectiveness of the stimulator with respect to energy transfer is proportional to the square root of the magnetic energy stored in the coil when the current in the coil reaches its maximum value. A simple model of a nerve fiber is to regard each node as a leaky capacitor that has to be charged. Measurements with electrical stimulation indicate that the time constant of this leaky capacitor is of the order of 150-300 µs. Therefore, for effective stimulation the current pulse into the node should be shorter than this (Hess, Mills, and Murray, 1987). For a short pulse in the coil less energy is required, but obviously there is a lower limit too.
22.5 ACTIVATION OF EXCITABLE TISSUE BY TIME-VARYING MAGNETIC FIELDS
The actual stimulation of excitable tissue by a time-varying magnetic field results from the flow of induced current across membranes. Without such flow a depolarization is not produced and excitation cannot result. Unfortunately, one cannot examine this question in a general sense but rather must look at specific geometries and structures. To date this has been done only for a single nerve fiber in a uniform conducting medium with a stimulating coil whose plane is parallel to the fiber (Roth and Basser, 1990).
 In the model examined by Roth and Basser, the nerve is assumed to be unmyelinated, infinite in extent and lying in a uniform unbounded conducting medium, the membrane is described by Hodgkin-Huxley equations. The transmembrane voltage Vm is shown to satisfy the equation
In the model examined by Roth and Basser, the nerve is assumed to be unmyelinated, infinite in extent and lying in a uniform unbounded conducting medium, the membrane is described by Hodgkin-Huxley equations. The transmembrane voltage Vm is shown to satisfy the equation
 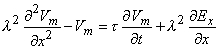 | (22.8) |
| where | Vm | = transmembrane voltage |
| λ | = membrane space constant | |
| τ | = membrane time constant | |
| x | = orientation of the fiber | |
| Ex | = x component of the magnetically induced electric field (proportional to the x component of induced current density). |
It is interesting that it is the axial derivative of this field that is the driving force for an induced voltage. For a uniform system in which end effects can be ignored, excitation will arise near the site of maximum changing current and not maximum current itself.
Barker AT, Freeston IL (1985): Medical applications of electric and magnetic fields. Electron. Power 31:(10) 757-60.
Barker AT, Freeston IL, Garnham CW (1990): Measurement of cortical and peripheral neural membrane time constant in man using magnetic nerve stimulation. J. Physiol. (Lond.) 423: 66.
Barker AT, Freeston IL, Jalinous R, Merton PA, Morton HB (1985): Magnetic stimulation of the human brain. J. Physiol. (Lond.) 369: 3P.
Barker AT, Garnham CW, Freeston IL (1991): Magnetic nerve stimulation - the effect of waveform on efficiency, determination of neural membrane time constants and the measurement of stimulator output. EEG & Clin. Neurophysiol. 43(Suppl.): .
Barker AT, Jalinous R, Freeston IL (1985): Non-invasive magnetic stimulation of human motor cortex. Lancet 1:(8437) 1106-7.
Bickford RG, Fremming BD (1965): Neuronal stimulation by pulsed magnetic fields in animals and man. In Digest of the 6th Internat. Conf. Medical Electronics and Biological Engineering, p. 112, IFMBE, .
d'Arsonval JA (1896): Dispositifs pour la mésure des courants alternatifs de toutes fréquences. C. R. Soc. Biol. (Paris) 2: 450-1.
Durand D, Ferguson AS, Dalbasti T (1992): Effect of surface boundary on neuronal magnetic stimulation. IEEE Trans. Biomed. Eng. 39:(1) 58-64.
Eaton H (1992): Electric field induced in spherical conductor from arbitrary coils: Application to magnetic stimulation and MEG. Med. & Biol. Eng. & Comput. 30:(July) 433-40.
Esselle KP, Stuchly MA (1992): Neural stimulation with magnetic fields: Analysis of induced electric fields. IEEE Trans. Biomed. Eng. 39:(7) 693-700.
Geddes LA (1991): History of magnetic stimulation of the nervous system. J. Clin. Neurophysiol 8: 3-9.
Hess CW, Mills KR, Murray NFM (1987): Magnetic brain stimulation: Central motor conduction studies in multiple sclerosis. Ann. Neurol. 22: 744-52.
Hess CW, Mills KR, Murray NMF (1986): Methodological considerations on the determination of central motor conduction time. In Proc. Of the Third Internat. Evoked Potential Symposium, ed. AB Person, CD Person,, Berlin-West.
Irwin DD, Rush S, Evering R, Lepeshkin E, Montgomery DB, Weggel RJ (1970): Stimulation of cardiac muscle by a time-varying magnetic field. IEEE Trans. Magn. Mag-6:(2) 321-2.
Lövsund P, Öberg PÅ, Nilsson SEG (1980): Magnetophosphenes: A quantitative analysis of thresholds. Med. & Biol. Eng. & Comput. 18: 326-34.
Malmivuo JA (1976): On the detection of the magnetic heart vector - An application of the reciprocity theorem. Helsinki Univ. Tech., Acta Polytechn. Scand., El. Eng. Series. Vol. 39, pp. 112. (Dr. tech. thesis)
Malmivuo JA (1980): Distribution of MEG detector sensitivity: An application of reciprocity. Med. & Biol. Eng. & Comput. 18:(3) 365-70.
Malmivuo JA (1992a): Distribution of electric current in inhomogeneous volume conductors. In Proceedings of the 8th Internat. Conference on Electrical Bio-Impedance, ed. T Lahtinen, pp. 18-20, University of Kuopio, Center for Training and Development, Kuopio, Finland.
Malmivuo JA (1992b): Distribution of stimulation fields in the tissue. In Proceedings of the First Ragnar Granit Symposium, ed. V Suihko, H Eskola, pp. 5-29, Tampere University of Technology, Ragnar Granit Institute, Tampere.
Malmivuo JA, Puikkonen J (1987): Sensitivity distribution of multichannel MEG detectors. In Abst. 6th Internat. Conf. Biomagnetism, Tokyo, 27-30 August, ed. K Atsumi, M Kotani, S Ueno, T Katila, SJ Williamson, pp. 112-3, Tokyo Denki University Press, Tokyo.
Mills KR, Murray NMF, Hess CW (1987): Magnetic and electrical transcranial brain stimulation: Physiological mechanisms and clinical applications. Neurosurg. 20: 164-8.
Polson MJ, Barker AT, Freeston IL (1982): Stimulation of nerve trunks with time-varying magnetic fields. Med. & Biol. Eng. & Comput. 20:(2) 243-4.
Porter R (1982): Neural events associated with movement performance. Proc. Aust. Physiol. Pharmacol. Soc. 13:(2) 31-46.
Rimpiläinen I, Eskola HJ, Häkkinen V, Karma P (1991): Transcranial facial nerve stimulation by magnetic stimulator in normal subjects. Electromyogr. Clin. Neurophysiol. 31: 259-63.
Rimpiläinen I, Laranne J, Eskola HJ, Häkkinen VK, Karma P (1990): Transcranial magnetic stimulation of the facial nerve in patients with Bell's palsy. Neurophysiol. Clin. 20: 85-7.
Rossi R, Puikkonen J, Malmivuo JA, Eskola HJ, Häkkinen V (1987): Magnetic stimulation - Design of a prototype and preliminary clinical experiments. Tampere Univ. Techn., Inst. Biomed. Eng., Reports 1:(6) 25.
Roth BJ, Basser PJ (1990): A model of the stimulation of a nerve fiber by electromagnetic induction. IEEE Trans. Biomed. Eng. 37:(6) 588-97.
Thompson SP (1910): A physiological effect of an alternating magnetic field. Proc. R. Soc. (Biol.) 82: 396-8.
Ueno S, Tashiro T, Harada K (1988): Localized stimulation of neural tissue in the brain by means of a paired configuration of time-varying magnetic fields. J. Appl. Phys. 64: 5862-4.
York DH (1987): Review of descending motor pathways involved with transcranial stimulation. Neurosurg. 20:(1) 70-3.
Öberg PÅ (1973): Magnetic stimulation of nerve tissue. Med. & Biol. Eng. & Comput. 11: 55-64.
 In the example considered by Roth and Basser the coil lies in the xy plane with its center at x = 0, y = 0, while the fiber is parallel to the x axis and at y = 2.5 cm and z = 1.0 cm. They consider a coil with radius of 2.5 cm wound from 30 turns of wire of 1.0 mm radius. The coil, located at a distance of 1.0 cm from the fiber, is a constituent of an RLC circuit; and the time variation is that resulting from a voltage step input. Assuming C = 200 µF and R = 3.0Ω, an overdamped current waveform results. From the resulting stimulation it is found that excitation results at x = 2.0 cm (or -2.0 cm, depending on the direction of the magnetic field) which corresponds to the position of maximum
In the example considered by Roth and Basser the coil lies in the xy plane with its center at x = 0, y = 0, while the fiber is parallel to the x axis and at y = 2.5 cm and z = 1.0 cm. They consider a coil with radius of 2.5 cm wound from 30 turns of wire of 1.0 mm radius. The coil, located at a distance of 1.0 cm from the fiber, is a constituent of an RLC circuit; and the time variation is that resulting from a voltage step input. Assuming C = 200 µF and R = 3.0Ω, an overdamped current waveform results. From the resulting stimulation it is found that excitation results at x = 2.0 cm (or -2.0 cm, depending on the direction of the magnetic field) which corresponds to the position of maximum  Ex /
Ex / x. The threshold applied voltage for excitation is determined to be 30 V. (This results in a peak coil current of around 10 A.) These design conditions could be readily realized.
x. The threshold applied voltage for excitation is determined to be 30 V. (This results in a peak coil current of around 10 A.) These design conditions could be readily realized.
 The effect of field risetime on efficiency of stimulation has been quantified (Barker, Freeston, and Garnham, 1990; Barker, Garnham, Freeston, 1991). Stimulators with short risetimes (< 60 µs) need only half the stored energy of those with longer risetimes (> 180 µs). The use of a variable field risetime also enables membrane time constant to be measured and this may contain useful diagnostic information.
The effect of field risetime on efficiency of stimulation has been quantified (Barker, Freeston, and Garnham, 1990; Barker, Garnham, Freeston, 1991). Stimulators with short risetimes (< 60 µs) need only half the stored energy of those with longer risetimes (> 180 µs). The use of a variable field risetime also enables membrane time constant to be measured and this may contain useful diagnostic information.
22.6 APPLICATION AREAS OF MAGNETIC STIMULATION OF NEURAL TISSUE
Magnetic stimulation can be applied to nervous stimulation either centrally or peripherally.
 The main benefit of magnetic stimulation is that the stimulating current density is not concentrated at the skin, as in electric stimulation, but is more equally distributed within the tissue. This is true especially in transcranial magnetic stimulation of the brain, where the high electric resistivity of the skull does not have any effect on the distribution of the stimulating current. Therefore, magnetic stimulation does not produce painful sensations at the skin, unlike stimulation of the motor cortex with electrodes on the scalp (Mills, Murray, and Hess,1986; 1988; Rimpiläinen et al., 1990, 1991).
The main benefit of magnetic stimulation is that the stimulating current density is not concentrated at the skin, as in electric stimulation, but is more equally distributed within the tissue. This is true especially in transcranial magnetic stimulation of the brain, where the high electric resistivity of the skull does not have any effect on the distribution of the stimulating current. Therefore, magnetic stimulation does not produce painful sensations at the skin, unlike stimulation of the motor cortex with electrodes on the scalp (Mills, Murray, and Hess,1986; 1988; Rimpiläinen et al., 1990, 1991).
 Another benefit of the magnetic stimulation method is that the stimulator does not have direct skin contact. This is a benefit in the sterile operation theater environment.
Another benefit of the magnetic stimulation method is that the stimulator does not have direct skin contact. This is a benefit in the sterile operation theater environment.
 As mentioned at the beginning of this chapter, the first papers introducing the clinical application of magnetic stimulation were published in 1985. Now magnetic stimulators for clinical applications are produced by several manufacturers. It may be predicted that the magnetic stimulation will be applied particularly to the stimulation of cortical areas, because in electric stimulation it is difficult to produce concentrated stimulating current density distributions in the cortical region and to avoid high current densities on the scalp.
As mentioned at the beginning of this chapter, the first papers introducing the clinical application of magnetic stimulation were published in 1985. Now magnetic stimulators for clinical applications are produced by several manufacturers. It may be predicted that the magnetic stimulation will be applied particularly to the stimulation of cortical areas, because in electric stimulation it is difficult to produce concentrated stimulating current density distributions in the cortical region and to avoid high current densities on the scalp.
REFERENCES



