23.1 STIMULATION OF CARDIAC MUSCLE
In Chapter 4 we described the behavior of excitable membranes both qualitatively and quantitatively through the Hodgkin-Huxley formalism. This lay the groundwork for Chapter 21 in which the response of nerve to electric stimulation was considered. This chapter considers the response of cardiac muscle to electric stimulation. It draws on these same fundamentals, but considers its particular application to the pacing and defibrillating of the heart (Greatbatch and Seligman, 1988; Tacker, 1988; El-Sherif and Samet, 1991). There are a number of significant differences that distinguish cardiac activation from the stimulation of nerve arising in FES (Chapter 22), and these are listed in Table 23.1. They come about first because of the size differences in these two cases. For stimulation of a nerve the target region is of the order of a few cubic millimeters, while the target region in the heart is in the order of a few cubic centimeters. For FES it is often necessary to achieve a finely graded response, entailing recruitment of fibers from small to large diameter. FES thus contrasts sharply with electric stimulation of cardiac tissue where a stimulus activates either the entire heart or none of it as a consequence of the syncytial structure. The large size of the heart usually means that excitable tissue whose excitation must be avoided can be excluded based on good spatial separation. In view of the cardiac syncytium the physical arrangement of stimulating electrodes is not in any way critical or demanding. One of the great challenges in FES is to devise ways to deal with fatigue; fortunately, heart muscle does not fatigue. However, all the advantages do not lie with cardiac muscle. We mention that care must be exercised that a pacemaker stimulus is not inadvertently delivered during the vulnerable period, or the serious consequence of fibrillation could result. This hazard does not arise in striated muscle.
There are a number of significant differences that distinguish cardiac activation from the stimulation of nerve arising in FES (Chapter 22), and these are listed in Table 23.1. They come about first because of the size differences in these two cases. For stimulation of a nerve the target region is of the order of a few cubic millimeters, while the target region in the heart is in the order of a few cubic centimeters. For FES it is often necessary to achieve a finely graded response, entailing recruitment of fibers from small to large diameter. FES thus contrasts sharply with electric stimulation of cardiac tissue where a stimulus activates either the entire heart or none of it as a consequence of the syncytial structure. The large size of the heart usually means that excitable tissue whose excitation must be avoided can be excluded based on good spatial separation. In view of the cardiac syncytium the physical arrangement of stimulating electrodes is not in any way critical or demanding. One of the great challenges in FES is to devise ways to deal with fatigue; fortunately, heart muscle does not fatigue. However, all the advantages do not lie with cardiac muscle. We mention that care must be exercised that a pacemaker stimulus is not inadvertently delivered during the vulnerable period, or the serious consequence of fibrillation could result. This hazard does not arise in striated muscle.
| Heart muscle | Striated muscle |
| Target region is large | Limited target region |
| Easy to avoid excitation of unwanted nerve | Excitable tissue to be avoided is close to target tissue |
| In effect, all cells are similar in size and excitability | Fibers vary in diameter, questions there are concerning recruitment, order of recruitment, and order that can differ from normal |
| Does not fatigue | Fatigue must be considered |
| Pulse-on-T | Does not fibrillate |
23.2 INDICATIONS FOR CARDIAC PACING
In Chapter 7 we described the normal cardiac conduction system. The heart's own pacemaker is located in the atrium and is responsible for initiation of the heartbeat. The heartbeat begins with activation of atrial tissue in the pacemaker region (i.e., the SA node), followed by cell-to-cell spread of excitation throughout the atrium. The only normal link of excitable tissue connecting the atria to the ventricles is the AV conduction system. Propagation takes place at a slow velocity, but at the ventricular end the bundles of His carry the excitation to many sites in the right and left ventricle at a relatively high velocity of 1-2 m/s. The slow conduction in the AV junction results in a delay of around 0.1 s between atrial and ventricular excitation; this timing facilitates terminal filling of the ventricles from atrial contraction prior to ventricular contraction. (Without a proper atrial contraction preceding the ventricular cardiac output may be reduced by 15%.) Disease affecting the AV junction may result in interference with normal AV conduction. This is described by different degrees of block. In first-degree block the effect is simply slowed conduction, in second-degree block there is a periodic dropped beat, but in third-degree block no signal reaches the ventricles. This latter condition is also referred to as complete heart block. In this case the ventricles are completely decoupled from the atria. Whereas the atrial heart rate is still determined at the AV node, the ventricles are paced by ectopic ventricular sites. Since under normal conditions the ventricles are driven by the atria, the latent ventricular pacemakers must have a lower rate. Consequently, in complete heart block the ventricles beat at a low rate (bradycardia). Even this condition may not require medical attention, but if the heart rate is too low, a condition known as Stokes-Adams syndrome, the situation becomes life-threatening. The prognosis in the case of complete heart block and Stokes-Adams is 50% mortality within one year. In this case the implantation of an artificial pacemaker is mandatory.
Disease affecting the AV junction may result in interference with normal AV conduction. This is described by different degrees of block. In first-degree block the effect is simply slowed conduction, in second-degree block there is a periodic dropped beat, but in third-degree block no signal reaches the ventricles. This latter condition is also referred to as complete heart block. In this case the ventricles are completely decoupled from the atria. Whereas the atrial heart rate is still determined at the AV node, the ventricles are paced by ectopic ventricular sites. Since under normal conditions the ventricles are driven by the atria, the latent ventricular pacemakers must have a lower rate. Consequently, in complete heart block the ventricles beat at a low rate (bradycardia). Even this condition may not require medical attention, but if the heart rate is too low, a condition known as Stokes-Adams syndrome, the situation becomes life-threatening. The prognosis in the case of complete heart block and Stokes-Adams is 50% mortality within one year. In this case the implantation of an artificial pacemaker is mandatory.
 Another condition, known as the sick sinus syndrome, is also one for which the artificial pacemaker is the treatment of choice. Here the bradycardia results from the atrial rate itself being abnormally low. Thus, even though the AV junction is normal, the ventricles are driven at too low a rate.
Another condition, known as the sick sinus syndrome, is also one for which the artificial pacemaker is the treatment of choice. Here the bradycardia results from the atrial rate itself being abnormally low. Thus, even though the AV junction is normal, the ventricles are driven at too low a rate.
23.3 CARDIAC PACEMAKER
23.3.1 Pacemaker Principles
We have noted previously the differences in stimulation of cardiac tissue in contrast to that of nervous tissue. Basically since the heart is an electric syncytium, excitation in any suitable region readily spreads throughout the entire heart. Furthermore, since the heart is a very large organ, the stimulating electrodes require no special design. And since there is a good separation from other excitable tissue, whatever necessary stimulation thresholds are required (times a safety factor), they can normally be fulfilled without excitation of other organs. The engineering challenges thus lie primarily in areas other than the classical electrophysiology described in previous chapters. These critical areas have to do, mainly, with logical decisions to provide or withhold pulses and/or to adjust their timing to make them as physiological as possible. The following sections are devoted to a description of the various practical aspects of pacemaker design and an elucidation of the points raised above. We consider the following topics:
The following sections are devoted to a description of the various practical aspects of pacemaker design and an elucidation of the points raised above. We consider the following topics:
 Control of impulses
Control of impulses
 Site of stimulation
Site of stimulation
 Excitation parameters and configuration
Excitation parameters and configuration
 Implantable energy sources
Implantable energy sources
 Electrodes.
Electrodes.
23.3.2 Control of Impulses
The earliest implantable pacemakers were designed to control the Stokes-Adams syndrome and for this purpose the simplest design is one where the ventricle is continuously stimulated at a safe rate. The pulse generator design required simply the generation of transthreshold pulses at the desired fixed heart rate. A pulse of about 2 ms duration, amplitude (essentially the battery voltage) of 5-8 V, and a frequency of 72 beats per minute were typically used. In general, the electrodes were sutured to the ventricle, and both electrodes and generator were implanted following a thoracotomy. This system has a number of shortcomings. First, it does not respond to the physiological needs for a variable heart rate depending on the body's oxygen requirements. (For example, these increase during exercise). Second, the patient may have only sporadic periods of Stokes-Adams syndrome. By pacing during regular ventricular activation, not only is there an unnecessary drain on implanted batteries but there is no coordination between the artificial stimulus and the naturally occurring one (in fact, this type of stimulation is called asynchronous). One potentially dangerous consequence is that the artificial stimulus might fall into the naturally occurring T-wave vulnerable period initiating tachycardia or fibrillation.
This system has a number of shortcomings. First, it does not respond to the physiological needs for a variable heart rate depending on the body's oxygen requirements. (For example, these increase during exercise). Second, the patient may have only sporadic periods of Stokes-Adams syndrome. By pacing during regular ventricular activation, not only is there an unnecessary drain on implanted batteries but there is no coordination between the artificial stimulus and the naturally occurring one (in fact, this type of stimulation is called asynchronous). One potentially dangerous consequence is that the artificial stimulus might fall into the naturally occurring T-wave vulnerable period initiating tachycardia or fibrillation.
 Particularly with the advent of integrated circuits it became possible to implant electronics that could sense the presence of an atrial and/or ventricular signal and to respond in an appropriate physiological way. For example, if the pathology is solely complete heart block, then the atrial pulse can be normal. An improved pacemaker design is one that senses the atrial excitation and delivers a ventricular pacing stimuli after a suitable delay (around 0.1 ms). An alternative was to sense the ectopic ventricular excitation, when it occurred. In its presence, an artificial stimulus was inhibited (or timed to coincide with the R wave). In the absence of a ventricular pulse, after a maximum acceptable delay, an artificial ventricular pulse was generated. Such pacemakers were termed a "demand" type.
Particularly with the advent of integrated circuits it became possible to implant electronics that could sense the presence of an atrial and/or ventricular signal and to respond in an appropriate physiological way. For example, if the pathology is solely complete heart block, then the atrial pulse can be normal. An improved pacemaker design is one that senses the atrial excitation and delivers a ventricular pacing stimuli after a suitable delay (around 0.1 ms). An alternative was to sense the ectopic ventricular excitation, when it occurred. In its presence, an artificial stimulus was inhibited (or timed to coincide with the R wave). In the absence of a ventricular pulse, after a maximum acceptable delay, an artificial ventricular pulse was generated. Such pacemakers were termed a "demand" type.
 In the mid-1970s pacemakers were being developed with programmable logic of this kind. A nomenclature code was developed to describe the particular logical pacemaker design implemented; this is reproduced in Table 23.2. (Although this code has been superseded by a more sophisticated one, it is still referred to in some current literature, and for this reason is included here.) The code consists of three letters: the first, giving the chamber paced (A = atrial, V = ventricular, and D = both, i.e., dual); the second, the chamber sensed; and the third, the type of response. Thus the asynchronous, fixed-rate, early type with ventricular pacing is simply V00. VVI describes the situation where a ventricular stimulus is inhibited if an acceptable intrinsic ventricular beat is sensed. In VAT, the atrial electrophysiology is normal; thus the atria is sensed and the ventricle triggered (after a suitable delay).
In the mid-1970s pacemakers were being developed with programmable logic of this kind. A nomenclature code was developed to describe the particular logical pacemaker design implemented; this is reproduced in Table 23.2. (Although this code has been superseded by a more sophisticated one, it is still referred to in some current literature, and for this reason is included here.) The code consists of three letters: the first, giving the chamber paced (A = atrial, V = ventricular, and D = both, i.e., dual); the second, the chamber sensed; and the third, the type of response. Thus the asynchronous, fixed-rate, early type with ventricular pacing is simply V00. VVI describes the situation where a ventricular stimulus is inhibited if an acceptable intrinsic ventricular beat is sensed. In VAT, the atrial electrophysiology is normal; thus the atria is sensed and the ventricle triggered (after a suitable delay).
| Chamber paced | Chamber sensed | Response | Description of mechanism |
|
V A D V V A A V D |
0 0 0 V V A A A V |
0 0 0 I T I T T I |
Fixed-rate ventricular pacing Fixed-rate atrial pacing Fixed-rate AV pacing Ventricular sensing and pacing, inhibited mode Ventricular sensing and pacing, triggered mode Atrial sensing and pacing, inhibited mode Atrial sensing and pacing, triggered mode Atrial sensing, ventricular pacing, triggered mode Ventricular sensing, AV pacing, inhibited |
23.3.3 Dual Chamber Multiprogrammable
The continued improvement in technology has made possible the implantation of microprocessors. This, coupled with improved technology, has permitted the placement of sensing/pacing leads routinely in both atria and ventricles. An important aspect of this improvement is in the power source, mainly the lithium battery, which significantly improves the available energy. The result is a much greater repertoire of electrophysiological behavior. An indication of this increased sophistication is the current pacemaker code. This consists of five letters. The first three are similar to the original ICHD code described in Table 23.2. The fourth and fifth letters are described in Table 23.3. These describe two additional functions of implantable pacemakers that have become possible with present technology.
| Fourth letter: rate modulation | Fifth letter: antiarrhythmia function | ||||||||||
| |||||||||||
|
Note: First, second, third letters as in Table 23.2 Source: Bernstein, et al. (1987) |
23.3.4 Rate Modulation
The natural heart rate is modulated by the sympathetic and parasympathetic central nervous systems. These respond to baroreceptor activity in the cardiovascular system, hypoxia, exercise, circulating catecholamines, and so on. Although it is impossible to devise a system that could respond to all of these, physiological control signals have been introduced that are believed significantly to evaluate the desired cardiac output. These include oxygen saturation (using optical methods), physical body movement, respiration rate, temperature, and so on. The introduction of rate modulation is, in effect, adaptive pacing to achieve more realistic physiological behavior and represents a higher level of sophistication than heretofore available. The goal is to keep the system as a whole in a reasonable physiological state. The fourth position in the NASPE/BPEG Code (Table 23.3) shows R if the system is capable of rate modulation, as described in the previous paragraph. When this feature is not present, this position describes the extent to which the pulse generator's operating values can be modified noninvasively. S (= Simple programmable) refers to the capability of adjusting the rate, output, or both; M (= Multiprogrammable) describes more extensive program capability; and C (= Communicating) the presence of some degree of telemetry. This degree of sophistication implies a multiprogrammable system. Similarly R (= Rate modulation) normally implies some degree of telemetry.
The fourth position in the NASPE/BPEG Code (Table 23.3) shows R if the system is capable of rate modulation, as described in the previous paragraph. When this feature is not present, this position describes the extent to which the pulse generator's operating values can be modified noninvasively. S (= Simple programmable) refers to the capability of adjusting the rate, output, or both; M (= Multiprogrammable) describes more extensive program capability; and C (= Communicating) the presence of some degree of telemetry. This degree of sophistication implies a multiprogrammable system. Similarly R (= Rate modulation) normally implies some degree of telemetry.
23.3.5 Anti-Tachycardia/Fibrillation
As we have seen, the pacemaker was originally devised to benefit patients with Stokes-Adams syndrome. The design requirements were simple and could be met with a fixed-rate pulse generator (mode V00). With the advent of increasingly sophisticated technology, the pacemaker functions were broadened and extended to patients with such conditions as sick sinus syndrome. An important additional category is patients with malignant tachycardia. These patients have occasional periods of tachycardia which can, if not treated, lead to fibrillation and death. Two main approaches are available. One consists of a set of rapid pacemaker pulses (approximately 20-30% faster than the tachycardia) delivered to the atria or ventricles. This may terminate the arrhythmia. The second approach entails the application of a shock of high energy with cardiac currents comparable to that present with external defibrillation. (A description of defibrillation systems, including implantable defibrillators, constitutes the material of Chapter 24). In the fifth position of the NASPE/BPEG code (Table 23.3), the anti-tachyarrhythmia function of the pacemaker is described. With P (= Pacing), low-energy stimulation (noted above), which is in the form of bursts, is present. S (= Shock) reflects the existence of a high-energy anti-tachyarrhythmia intervention capability for cardioversion or defibrillation. D (= Dual) describes both high- and low-energy intervention. Many believe that permanent pacing for ventricular tachycardia is too hazardous since it can lead to unstable ventricular tachycardia or even ventricular fibrillation. For these possibilities a shock backup presence is deemed essential. (An exception is physician-activated pacing which, in the presence of the physician, is used as an adjunctive therapy for sustained ventricular tachycardia.) For this purpose noninvasive activation is achieved by a magnet or rf telemetry.
In the fifth position of the NASPE/BPEG code (Table 23.3), the anti-tachyarrhythmia function of the pacemaker is described. With P (= Pacing), low-energy stimulation (noted above), which is in the form of bursts, is present. S (= Shock) reflects the existence of a high-energy anti-tachyarrhythmia intervention capability for cardioversion or defibrillation. D (= Dual) describes both high- and low-energy intervention. Many believe that permanent pacing for ventricular tachycardia is too hazardous since it can lead to unstable ventricular tachycardia or even ventricular fibrillation. For these possibilities a shock backup presence is deemed essential. (An exception is physician-activated pacing which, in the presence of the physician, is used as an adjunctive therapy for sustained ventricular tachycardia.) For this purpose noninvasive activation is achieved by a magnet or rf telemetry.
23.4 SITE OF STIMULATION
In the early pacemaker models, electrodes were sutured directly to the heart and the wires led to the pulse generators which were placed in a thoracic or abdominal pocket. But to avoid the trauma of a thoracotomy electrodes were increasingly placed in the heart cavities through a transvenous route. (The term transvenous while very popular, is a misnomer since it actually refers to the threading of electrodes through a vein into the right atria and/or ventricle). At present, around 95% of pacemaker electrodes are endocardial. Several veins are and have been used, including, typically, the subclavian, cephalic, and external jugular. The electrodes are manipulated by a stiff stylet wire from the distal end under fluoroscopic visualization. The right atrial electrode is hooked into the right atrial appendage, whereas the right ventricular electrode lies at the right ventricular apex position. The electrode tips are fabricated with tines that lodge in the right ventricular trabeculation and the right atrial appendage for stabilization. (Also, after removal of the stylet wire, the atrial lead curves into a J shape that adds additional stabilization.) The pulse generator is usually placed in a prepectoral location. From an electrophysiological standpoint, the actual location of the ventricular myocardial or endocardial electrode is not important. From the right heart position the activation wave must resemble that in left bundle branch block and reflect mainly cell-to-cell conduction. The hemodynamic consequence is that a satisfactory cardiac output is achieved. Experiments also show that the threshold stimulating currents do not vary widely, suggesting a certain symmetry between current source and depolarization achieved. One can in fact set up a very simplified ideal model based on the bidomain model of Chapter 9, and this is done in the following section.
From an electrophysiological standpoint, the actual location of the ventricular myocardial or endocardial electrode is not important. From the right heart position the activation wave must resemble that in left bundle branch block and reflect mainly cell-to-cell conduction. The hemodynamic consequence is that a satisfactory cardiac output is achieved. Experiments also show that the threshold stimulating currents do not vary widely, suggesting a certain symmetry between current source and depolarization achieved. One can in fact set up a very simplified ideal model based on the bidomain model of Chapter 9, and this is done in the following section.
23.5 EXCITATION PARAMETERS AND CONFIGURATION
In Section 9.5 we considered the induced transmembrane potential from a point current source in a homogeneous isotropic bidomain. This result can be readily modified to the present case where the electrode has a finite radius a. Because of the spherical symmetry the fields vary with r only. At r = a we require that
 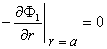 | (23.1) |
since the current leaving the electrode enters the interstitial space only. In fact, the boundary condition in the interstitial space is that the total current entering this space at r = a is the total applied current Ia. In view of Equation (23.1) and the definition of Vm then at r = a we have
 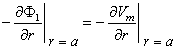 | (23.2) |
Consequently, the aforementioned boundary condition is
 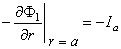 | (23.3) |
| where | 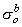 | = interstitial bidomain conductivity, as described in Equation 9.17 |
| Ia | = applied current, assumed to be cathodal (hence the minus sign) |
Now Equation 9.28 describes the behavior of Vm in the region r  a under steady-state conditions (namely
a under steady-state conditions (namely 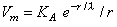 ). If this is substituted into Equation 23.3 and solved for the coefficient KA we obtain
). If this is substituted into Equation 23.3 and solved for the coefficient KA we obtain
 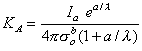 | (23.4) |
Substituting this back into Equation 9.28 gives an expression for Vm, namely
 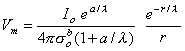 | (23.5) |
 The maximum induced voltage is at r = a; in this case, Equation 23.5 reduces to Vm max or
The maximum induced voltage is at r = a; in this case, Equation 23.5 reduces to Vm max or
 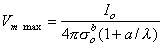 | (23.6) |
One notes from Equation 23.6 that the smaller the electrode the larger the induced voltage. For electrodes that are large compared with the space constant, the induced voltage varies inversely as the square of the electrode radius; but when the radius is much smaller than the space constant, the voltage varies only as the first power of the inverse radius.
 With an endocardial lead the electrode is surrounded by cardiac tissue on one side and blood on the other. Since the blood conductivity is about three times greater than cardiac tissue, in our very simple isotropic model the applied current should possibly be reduced by some factor over what it would be in the assumed uniform model developed in Chapter 9 and extended above. We have chosen this factor to be around 35%. For a 1 ms stimulus pulse the membrane should come close to the assumed steady-state value (Cartee, 1991). Equation 23.6 gives the maximum steady-state induced voltage if we identify a as the equivalent radius of the (spherical) electrode. A fairly typical electrode has an area of 8.8 mm≤ (Breivik, Hoff, and Ohm, 1985). This is converted into a sphericalized radius of 1.2 mm as described in Miller et al. (1985). We also choose the space constant as λ = 0.5 mm (Plonsey and Barr, 1982), and assign
With an endocardial lead the electrode is surrounded by cardiac tissue on one side and blood on the other. Since the blood conductivity is about three times greater than cardiac tissue, in our very simple isotropic model the applied current should possibly be reduced by some factor over what it would be in the assumed uniform model developed in Chapter 9 and extended above. We have chosen this factor to be around 35%. For a 1 ms stimulus pulse the membrane should come close to the assumed steady-state value (Cartee, 1991). Equation 23.6 gives the maximum steady-state induced voltage if we identify a as the equivalent radius of the (spherical) electrode. A fairly typical electrode has an area of 8.8 mm≤ (Breivik, Hoff, and Ohm, 1985). This is converted into a sphericalized radius of 1.2 mm as described in Miller et al. (1985). We also choose the space constant as λ = 0.5 mm (Plonsey and Barr, 1982), and assign 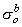 (the interstitial conductivity as defined in Equation 9.17) the value of .002 S/cm. Then
(the interstitial conductivity as defined in Equation 9.17) the value of .002 S/cm. Then
 Vm max = 34 ∑ Ia Vm max = 34 ∑ Ia | (23.7) |
| where | Ia | = applied cathodal current [mA] |
| Vm max | = membrane voltage [mV] |
 If Ia is 0.44 mA, then Vm is 15.0 mV, which is not an unreasonable threshold voltage, considering the many approximations in this simple, homogeneous, isotropic model. The result is in the range of published measurements (Breivik, Hoff, and Ohm, 1985) and the empirical current threshold value of 0.05 mA/mm≤ (Tarjan, 1991). Based on Equation 23.6 the use of a smaller-sized electrode will diminish the required current for a given threshold transmembrane voltage, as noted above. There is a limit to the amount by which the electrode size can be decreased. The reason is that one has to reach the required threshold current with a fixed battery voltage, and this limits the maximum allowable circuit impedance. The latter, however, is mainly the electrode-tissue impedance, which increases inversely with the electrode radius. In a practical design one should also include the possible effect of growth of fibrous tissue around the electrode since this will increase the size of the effective radius a in Equation 23.6 (see Section 23.7). We note that in Equation 23.6, Vm is positive (depolarization) for an assumed cathodal (monopolar) electrode.
If Ia is 0.44 mA, then Vm is 15.0 mV, which is not an unreasonable threshold voltage, considering the many approximations in this simple, homogeneous, isotropic model. The result is in the range of published measurements (Breivik, Hoff, and Ohm, 1985) and the empirical current threshold value of 0.05 mA/mm≤ (Tarjan, 1991). Based on Equation 23.6 the use of a smaller-sized electrode will diminish the required current for a given threshold transmembrane voltage, as noted above. There is a limit to the amount by which the electrode size can be decreased. The reason is that one has to reach the required threshold current with a fixed battery voltage, and this limits the maximum allowable circuit impedance. The latter, however, is mainly the electrode-tissue impedance, which increases inversely with the electrode radius. In a practical design one should also include the possible effect of growth of fibrous tissue around the electrode since this will increase the size of the effective radius a in Equation 23.6 (see Section 23.7). We note that in Equation 23.6, Vm is positive (depolarization) for an assumed cathodal (monopolar) electrode.
 When the electrode is monopolar, the reference electrode is invariably chosen as the case of the pulse generator unit. The main advantage of the monopolar system is that only a single electrode wire (per chamber) has to be implanted. For endocardial leads this smaller size compared to a bipolar lead is clearly desirable. In addition, it also represents a smaller wire lying in the tricuspid valve, through which the catheter electrode must run. One of the disadvantages, though, is the presence of stimulating current throughout a large part of the thorax; thus striated muscles lying in this region may be stimulated, giving rise to annoying muscle twitch. Both the phrenic and diaphragmatic nerves have also been known to be affected.
When the electrode is monopolar, the reference electrode is invariably chosen as the case of the pulse generator unit. The main advantage of the monopolar system is that only a single electrode wire (per chamber) has to be implanted. For endocardial leads this smaller size compared to a bipolar lead is clearly desirable. In addition, it also represents a smaller wire lying in the tricuspid valve, through which the catheter electrode must run. One of the disadvantages, though, is the presence of stimulating current throughout a large part of the thorax; thus striated muscles lying in this region may be stimulated, giving rise to annoying muscle twitch. Both the phrenic and diaphragmatic nerves have also been known to be affected.
 The bipolar electrode has an electric field that varies as 1/r≥ rather than 1/r≤ and, consequently, is less likely to affect excitable tissues remote from the site at which the electrodes have been placed. In addition, when these electrodes are used in the sensing mode, the bipolar configuration is less sensitive to interference from distant extraneous signals. Such electromagnetic interference may at times be mistaken for a cardiac signal and incorrect logical inferences drawn by a multiprogrammable pacemaker. With present technology the advantage of handling a single versus double wire per chamber is no longer very great. For more historical reasons unipolar systems are favored in the United States, whereas European systems favor bipolar.
The bipolar electrode has an electric field that varies as 1/r≥ rather than 1/r≤ and, consequently, is less likely to affect excitable tissues remote from the site at which the electrodes have been placed. In addition, when these electrodes are used in the sensing mode, the bipolar configuration is less sensitive to interference from distant extraneous signals. Such electromagnetic interference may at times be mistaken for a cardiac signal and incorrect logical inferences drawn by a multiprogrammable pacemaker. With present technology the advantage of handling a single versus double wire per chamber is no longer very great. For more historical reasons unipolar systems are favored in the United States, whereas European systems favor bipolar.
23.6 IMPLANTABLE ENERGY SOURCES
At the time of the development of the early pacemakers the battery with longest life was the zinc-mercury battery. This was adopted for pacemaker use, but even as late as 1970 the best that could be achieved, on average, was a 2 year life-span. A second problem with the zinc-mercury cell is liberation of hydrogen gas at high pressure (300 psi). A consequence is the inability to create a hermetical seal of the cell. By 1970 the limiting step in pacemaker longevity was this power source.
 A very wide range of power sources for pacemakers have been proposed and investigated. These include schemes that utilize the body's own chemistry and energy. For example, the energy from the beating heart itself was investigated. Various types of fuel cells were considered. None have been actually used clinically. In addition, rechargeable systems using external power sources coupled through the body tissue have been tried, but very few have actually been used.
A very wide range of power sources for pacemakers have been proposed and investigated. These include schemes that utilize the body's own chemistry and energy. For example, the energy from the beating heart itself was investigated. Various types of fuel cells were considered. None have been actually used clinically. In addition, rechargeable systems using external power sources coupled through the body tissue have been tried, but very few have actually been used.
 A major breakthrough was the introduction of the lithium battery, which is now used in virtually all new pacemaker systems. The reaction involves lithium and iodine:
A major breakthrough was the introduction of the lithium battery, which is now used in virtually all new pacemaker systems. The reaction involves lithium and iodine:
 2Li + I2 2Li + I2  2LiI 2LiI | (23.8) |
Since no gas is produced, the lithium cell can be hermetically sealed. Furthermore the serious problem of breakdown of the separator in the zinc-mercury battery does not arise in the lithium-iodine cell since, in the latter, the separator forms spontaneously and is self-healing. The lithium battery also has a reliable end-of-life decay characteristic which fails slowly enough to permit its detection in a normal checkup and the scheduling of a timely replacement. In addition to these attractive features, the approximate 50% survival of the lithium-iodine battery is 12 years (Bernstein, 1991).
23.7 ELECTRODES
The pacemaker system consists of a package containing the pulse generator and pulse-sensing elements along with the associated logic circuits and the battery; this package is connected by leads to the electrodes themselves. The leads carry heart signals from the heart to the electronics and current stimuli to the heart. While simple in function, the latter components have posed challenging engineering problems.
 The leads are insulated wires that must carry current with low resistance and be capable of reliable operation for many years in spite of repeated flexing. The use of hard flexible metals is reguired. Early leads were twisted or braided strands placed in a hollow catheter. At present, in the United States a helical coiled lead is favored, which is put into position by a stylet wire. This shape converts the various types of body and heart movement into torsion, which the metal can easily tolerate. The coil may be made of stainless steel, Eigiloy, or MP35N, all of which are alloys with excellent strength. The insulating materials that have proven best are silicone rubber and polyurethane.
The leads are insulated wires that must carry current with low resistance and be capable of reliable operation for many years in spite of repeated flexing. The use of hard flexible metals is reguired. Early leads were twisted or braided strands placed in a hollow catheter. At present, in the United States a helical coiled lead is favored, which is put into position by a stylet wire. This shape converts the various types of body and heart movement into torsion, which the metal can easily tolerate. The coil may be made of stainless steel, Eigiloy, or MP35N, all of which are alloys with excellent strength. The insulating materials that have proven best are silicone rubber and polyurethane.
 The electrodes themselves are also, usually, an alloy. Surface preparation is important since microcracks can become a site of local currents and corrosion. A series capacitance is always used to eliminate any DC-current flow and achieve the balanced biphasic condition discussed in Chapter 21. The use of porous electrodes has also been suggested to improve ingrowth of tissue and stabilization of the electrode. The endocardial electrode generally becomes encased in collagen. Using Equation 23.6 we can consider that this increases the effective electrode radius, hence decreasing the stimulating voltage, for a given current source. A typical capsule thickness of 0.6 mm (Miller et al., 1985) increases a from 1.2 to 1.8 mm in the illustrative example leading to Equation 23.7. The result is a change of coefficient in Equation 23.7:
The electrodes themselves are also, usually, an alloy. Surface preparation is important since microcracks can become a site of local currents and corrosion. A series capacitance is always used to eliminate any DC-current flow and achieve the balanced biphasic condition discussed in Chapter 21. The use of porous electrodes has also been suggested to improve ingrowth of tissue and stabilization of the electrode. The endocardial electrode generally becomes encased in collagen. Using Equation 23.6 we can consider that this increases the effective electrode radius, hence decreasing the stimulating voltage, for a given current source. A typical capsule thickness of 0.6 mm (Miller et al., 1985) increases a from 1.2 to 1.8 mm in the illustrative example leading to Equation 23.7. The result is a change of coefficient in Equation 23.7:
 Vm max = 16.8 ∑ Ia Vm max = 16.8 ∑ Ia | (23.9) |
This amounts to a reduction in the stimulus strength by 2.0. In fact in experimental studies, one finds that the initial threshold at the time of placement of a ventricular pacing lead increases by factors of 2-4 over the following period (Miller et al., 1985).
Bernstein AD (1991): Classification of cardiac pacemakers. In Cardiac Pacing and Electrophysiology, 3rd ed., ed. N El-Sherif, P Samet, pp. 494-503, W.B. Saunders, Philadelphia.
Bernstein AD, Camm AJ, Fletcher RD, Gold RD, Rickards AF, Smyth NPD, Spielman SR, Sutton R (1987): The NASPE/BPEG generic pacemaker code for antibradyarrhythmia and adaptive-rate pacing and antitachyarrhythmia devices. PACE, Pacing Clin. Electrophysiol. 10: 794-9.
Bourland JD, Mouchawar GA, Nyenhuis JA, Geddes LA, Foster KS, Jones JT, Graber GP (1990): Transchest magnetic (eddy-current) stimulation of the dog heart. Med. & Biol. Eng. & Comput. 28: 196-8.
Breivik K, Hoff PI, Ohm OJ (1985): In favor of bipolar ventricular leads. In Pacemaker Leads, ed. AE Aubert, H Ector, pp. 33-8, Elsevier, Amsterdam.
Cartee LA, Plonsey R (1992): The transient subthreshold response of spherical and cylindrical cell models to extracellular stimulation. IEEE Trans. Biomed. Eng. 39: 76-85.
El-Sherif N, Samet P (eds.) (1991): Cardiac Pacing and Electrophysiology, 3rd ed., 784 pp. Saunders, Philadelphia.
Greatbatch W, Seligman LJ (1988): Pacemakers. In Encyclopedia of Medical Devices and Instrumentation, ed. JG Webster, pp. 2175-203, John Wiley & Son, New York.
Irwin DD, Rush S, Evering R, Lepeshkin E, Montgomery DB, Weggel RJ (1970): Stimulation of cardiac muscle by a time-varying magnetic field. IEEE Trans. Magn. Mag-6:(2) 321-2.
Miller SL, Mac Gregor DC, Margules ES, Bobyn JD, Wilson GJ (1985): Theoretical justification for size reduction of porous-surfaced electrodes. In Pacemaker Leads, ed. AE Aubert, H Ector, pp. 57-62, Elsevier, Amsterdam.
Mouchawar GA, Bourland JD, Nyenhuis JA, Geddes LA, Foster KS, Jones JT, Graber GP (1992): Closed-chest cardiac stimulation with a pulsed magnetic field. Med. & Biol. Eng. & Comput. 30:(2) 162-8.
Parsonnet V, Furman S, Smyth N (1974): Implantable cardiac pacemakers. Am. J. Cardiol. 34: 487-500.
Plonsey R, Barr RC (1982): The four-electrode resistivity technique as applied to cardiac muscle. IEEE Trans. Biomed. Eng. BME-29: 541-6.
Tacker WA (1988): Electrical defibrillators. In Encyclopedia of Medical Devices and Instrumentation, Vol. 2, ed. JG Webster, pp. 939-44, John Wiley & Sons, New York.
Tarjan PP (1991): Engineering aspects of modern cardiac pacing. In Cardiac Pacing and Electrophysiology, 3rd ed., ed. N El-Sherif, P Samet, pp. 484-93, W.B. Saunders, Philadelphia.
23.8 MAGNETIC STIMULATION OF CARDIAC MUSCLE
Several experiments with magnetic stimulation of cardiac muscle have been reported (Bourland et al., 1990; Irwin et al., 1970; Mouchawar et al., 1992).
 In their experiments, Mouchawar et al. (1992) used two coplanar stimulation coils placed close to the heart of an anesthetized dog. The coils had an outer radius of 8.5 cm, a thickness of 1.25 cm, and included 30 turns. The distance from the coils to the ventricles within the chest ranged from 2 to 3.5 cm. The magnetic stimulator produced an ectopic beat in the vagal-arrested dogs with an average energy of approximately 12 kJ. This is much higher than the energy needed to stimulate magnetically the human peripheral nervous system, which requires typically 400 J.
In their experiments, Mouchawar et al. (1992) used two coplanar stimulation coils placed close to the heart of an anesthetized dog. The coils had an outer radius of 8.5 cm, a thickness of 1.25 cm, and included 30 turns. The distance from the coils to the ventricles within the chest ranged from 2 to 3.5 cm. The magnetic stimulator produced an ectopic beat in the vagal-arrested dogs with an average energy of approximately 12 kJ. This is much higher than the energy needed to stimulate magnetically the human peripheral nervous system, which requires typically 400 J.
REFERENCES



