Sensitivity Distribution Visualizations of Impedance Tomography Measurement Strategies Pasi Kauppinen, Jari Hyttinen, Jaakko Malmivuo Ragnar Granit Institute, Tampere University of Technology, Tampere, Finland Correspondence: P Kauppinen, Ragnar Granit Institute, Tampere University of Technology, Abstract.As reconstruction of images in electrical impedance tomography (EIT) is sensitive to noise, low signal level and small errors in measured data result into large errors in final images. In order to optimize the signal acquisition from any region, measurement should possess the highest sensitivity and selectivity in that region. This study was conducted to illustrate measurement properties of various generally applied measurement strategies in EIT. Computer models were utilized in simulating the sensitivity distributions of neighboring, cross, opposite and adaptive methods in simplified volume conductors. Animation sequences of visualized sensitivity fields were created for each method. Highest sensitivity values were obtained with the cross and opposite methods, while neighboring was the least sensitive, when investigating a single measurement. Maximum proportional selectivities in the centre of a 2D model were 100, 94, 88 and 62 %, respectively, as compared between the neighboring, cross, opposite and adaptive methods. In 3D, the corresponding values were 100, 55, 50 and 7.6 %. Regions of negative sensitivity were detected, which in part complicates the reconstruction. Nevertheless, studying sensitivity distributions may improve the basic understanding of the technique and help improving the outcome of EIT in the future. Keywords:Electrical Impedance Tomography; Sensitivity Distribution; Measurement Properties; Modelling; Lead Field; Computer Simulation; Electrode Configuration 1. Introduction Electrical impedance tomography (EIT) aims to produce static or dynamic images related to the conductivity distribution of the measured region. The advantages of EIT as compared to conventional imaging techniques such as computed tomography or magnetic resonance imaging are: It is considered safe by merit of the small alternating currents required; it can be used as a long-term, continuous imaging method; and the system can be constructed at low cost and in portable size [Zhu et al., 1993]. The range of EIT possible applications in medicine is wide. Brown [1990] reports that potential medical applications of the technique include the following of gastric function, lung ventilation imaging, tissue temperature imaging, lung water imaging, blood vessel distension, pelvic congestion, lung perfusion and cardiopulmonary function, cerebral blood flow, thoracic fluid determination, cell death imaging in radiotherapy, following of bladder filling, gastric movement imaging and tumor imaging. More recently, promising results have been obtained in neurological EIT, where applications in epilepsy, stroke and neuronal depolarization are encouraging [Holder, 2005]. However, a clinical breakthrough of EIT into routine use is still ahead. At present, its major disadvantage is poor spatial resolution, which decreases especially in deeper regions of medium. |
| IJBEM, 2006, Vol. 8, No. 1 | Page VII/2 |
|
The ability of EIT to show changes in conductivity is superior to its ability to show absolute values of the conductivity, therefore often producing dynamic images. The spatial contribution of a conductivity distribution to an impedance measurement depends on the current injection and the associated voltage measurement configuration. For this, a number of data acquisition strategies exist for EIT. In ideal conditions, however, the only required data is the independent tetrapolar data associated with the number of electrodes used. With these data, all other excitation/measurement combinations may be derived off-line [Malmivuo and Plonsey 1995; Kauppinen et al., 1999]. Data acquisition of such data is relatively simple and no special excitation patterns (e.g. multisite adaptive ones) are needed. Yet, as reconstruction techniques generating EIT images are sensitive to noise, small errors in the measured data translate into large errors in the resulting images, hindering the use of independent data. In order to optimize the signal acquisition from any region, measurement should possess the highest detection capacity in that region. Contribution from any region to the measurement is not self-evident; the sensitivity distribution of the measurement may also contain negative values [Geselowitz 1971; Kauppinen et al., 1999], which in part may complicate the interpretation of measured data. This has proven to be especially complicated in impedance cardiography (ICG), where typically a single time-domain signal is acquired and physiological variables are derived from that waveform [Kauppinen 1999]. The concept of sensitivity distribution, or merely inverted sensitivity matrix, has been used in the EIT inverse solution. The sensitivity matrix contains a sensitivity distribution in each row for each measurement setup used. However, according to our knowledge, visualizations of these data have not been published by other groups [Kauppinen et al., 2005]. Quite the contrary, illustrations showing only the current distribution, that may even give erroneous impression of what the EIT actually measures, have been published [e.g. Malmivuo and Plonsey 1995; Liston et al., 2002;Grimnes and Martinsen, 2000]. We conducted an illustrative computer model study in order to investigate the form of sensitivity distributions in various EIT measurement strategies by applying the lead field theoretical approach. The purpose of the simulation study reported in this paper is to gain further understanding of the measurement properties of EIT measurement and hence aid in understanding the methodology. Common EIT measurement methods were simulated and visualized with homogeneous 2D and 3D radially symmetrical computer models. Additional experiments were conducted with a 2D model mimicking the anatomy of the human head. 2. Material and Methods 2.1. Sensitivity Distribution Sensitivity distribution of an impedance measurement gives a relation between the measured impedance Z (and change in it) caused by a given conductivity distribution (and its change). It describes how effectively each region is contributing to the measured impedance signal. If conductivity change is not involved, the measured impedance is obtained with
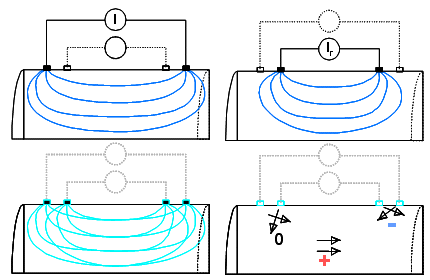
where JLE and JLI obtained with reciprocal energization, are the current density fields (i.e. impedance lead fields) associated with the current injection and voltage measurement leads [Geselowitz, 1971; Malmivuo and Plonsey, 1995]. This equation gives the contribution from each volume to the total Z, and the dot product of the two fields expresses the sensitivity to conductivity changes throughout the volume conductor. Effects of conductivity changes on measured impedance can be calculated by ΔZ = Z(t2) - Z(t1), where the time instants t1 and t2 refer to situations before and after a conductivity change, with the assumption that the changes in the lead fields are negligible due to the small conductivity change. As the resulting scalar field may possess positive and negative values depending on the orientation of the two lead fields, the measured impedance may either increase, decrease or be entirely unaffected in consequence of a conductivity change in a particular region. Fig. 1 illustrates schematically the formation of the measurement sensitivity of a tetrapolar impedance measurement in a homogeneous cylinder. Electrode distances affect whether superficial or deep regions are more efficiently sampled and the regions of negative sensitivity (as depicted by Eq. 1) lay near the electrodes, where the two lead fields have antiparallel components. |
| IJBEM, 2006, Vol. 8, No. 1 | Page VII/3 |
|
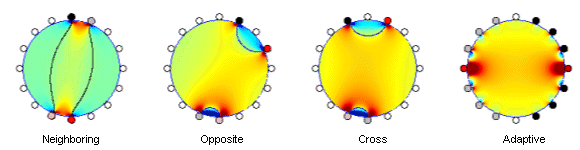
To analyze the capacity of an EIT measurement to detect conductivity and its changes in the centre region, the sensitivity in this region of interest may be evaluated. Another parameter describing the measurement is selectivity, which gives the proportional value of the sensitivity in the target region against the total sensitivity over the medium. The difficulty is that an ideal measurement should have both high sensitivity and high selectivity simultaneously, which would require lead fields having null values anywhere else than in the target region. This, however, is practically impossible to achieve for any surface electrode system. Figure 1. Simplified sensitivity distribution of a four-electrode impedance measurement applied to a uniform conductive cylinder. (a) The lead field produced by the current excitation electrodes (Ir refers to reciprocal current injection). (b) The field which would be produced if current were driven through voltage measurement electrodes. (c) Superimposed fields of the previous two lead fields. (d) Principled presentation of the sensitivity of the measurement setup in a few locations. 2.2. EIT Measurement Strategies Several EIT data collection strategies, i.e. collections of current injection and voltage measurement pairs, have been published. Here, animated illustrations of the principle of four strategies addressed in [Malmivuo and Plonsey, 1995] are given. Black electrode locations are used for current delivery and red ones for voltage detection in the following animations. Neighboring Method In the neighboring method [Brown and Segar, 1987], the current is applied through neighboring electrodes and the voltage measured successively from all other adjacent electrode pairs. All current electrode pairs will be used sequentially, producing 16 current injection patterns when 16 electrodes are used. Animations. Neighboring method
The number of tetrapolar independent measurements for the method is
Cross Method The cross method aims to produce more homogeneous fields than the neighboring method. This is obtained by using more distant electrodes instead of the adjacent ones [Hua et al., 1987]. |
| IJBEM, 2006, Vol. 8, No. 1 | Page VII/4 |
|
Animations. Cross method The number of tetrapolar independent measurements is
Opposite Method In opposite method, the current is injected through two diametrically opposed electrodes. This evidently should produce more field strength in the deeper regions of the medium. Animations. Opposite method
The number of tetrapolar independent measurements is
Adaptive Method Adaptive method enables simultaneous current flow from all the electrodes. The idea is to optimize the current patterns in terms of maximizing the resulted voltage measurements for desired regions. Several methods have been introduced to derive these optimal patterns [Holder, 2005]. Here, a basic trigonometric current injection is used, which should produce homogeneous distribution in homogeneous radially symmetric medium [see additional explanation in e.g. Malmivuo and Plonsey, 1995]. Animations. Adaptive method
The number of tetrapolar independent measurements with the trigonometric current pattern (note, that several other patterns may be used with the adaptive method, depending on the EIT algorithm and instrumentation applied) is
2.3. FDM Models Methods to construct and solve accurate volume conductor computer models based on the finite difference method (FDM) have previously been developed and validated [Kauppinen et al., 1999b]. The VCMT software package utilized affords the construction of a model from segmented voxel anatomy without limitations on the number of different tissue types and their distribution. The simulation result is provided in each discrete element in the model, not only at the boundaries of inhomogeneities as in BEM or FEM often applied in EIT. The major drawback is the inefficiency of the solver routine, which is based on an iterative over-relaxation technique. For calculating the lead fields of 16 electrode EIT setups in a simple case illustrating the basic form of the sensitivity distribution, two homogeneous models were applied: a) 2D slice (2 mm height), diameter 249 mm. Number of computational nodes 98 528, element size 1*1*1 mm b) 3D cylinder, height 300 mm, diameter 249 mm. Number of nodes 88 896, element size 3 * 3 * 20 mm. An additional model (2D) was derived from a realistic geometry model representing major tissues of the human head. |
| IJBEM, 2006, Vol. 8, No. 1 | Page VII/5 |
|
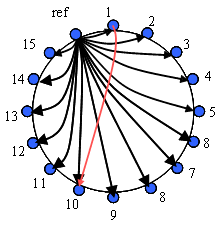
2.4. Simulations and Analyses The number of electrodes was 16 in the present study, which allows 195 (15*13) tetrapolar impedance measurement configurations, including the reciprocal measurements. For each model, 15 simulations were run to obtain lead field of each electrode against a common reference. This set of the lead fields is the only simulation data required. Figure 2. Original set of 15 simulated lead fields. Using these data, new lead fields may be calculated directly by linear combination, e.g. lead field between the electrode locations 1 and 10 is obtained by substracting lead field ref->1 from the lead field ref->10 (as shown by the red arrow). Deriving any EIT excitation/measurement combination with these pre-calculated lead fields is a simple non-iterative calculation, since the system is assumed to be linear. E.g. a lead field between the electrode locations 1 and 10 as shown in Fig. 2 may be obtained by subtracting lead field ref->10 from the ref->1. The resulting measurement sensitivity distribution given by Eq. 1 can therefore be calculated without time-consuming simulations for each measurement combination studied. The studied acquisition methods were neighboring, opposite, cross and adaptive ones. Due to the symmetry and homogeneity of the medium (2D slice and 3D cylinder), only limited number of measurement combinations were derived and analyzed: The sensitivity pattern is similar, only rotated, in other combinations not calculated. Sensitivity and proportional selectivity in the centre of the models were obtained and compared between the methods. Additional experiments were conducted on a single slice realistic model of the head. These experiments were only preliminary to visualize the effects of more realistic geometry and conductivity distribution on EIT sensitivity fields. 3. Results Calculated maximum sensitivities and selectivities in the centre of the model are given in Table 1 for each method. For the reason of comparison, the values are given in percentages as compared against each method so that the maximum value for a parameter is 100 %. Also, the simulated basal Z for the most responsive measurements are given. The number of processed sensitivity distributions was altogether 477.
Table 1. Proportional sensitivities and selectivities in the centre for each method evaluated between the EIT measurement strategies with 2D and 3D models.
|
| IJBEM, 2006, Vol. 8, No. 1 | Page VII/6 |
|
As the sensitivity is evaluated at a single pixel/voxel in the centre of the model, high values are related almost linearly to high basal Z readings. Selectivity, on the other hand, gains higher values when the contribution from the other regions is reduced. This, at least in the homogeneous models studied, tends to result in smaller basal Z values as seen in Table 1. Animations 13 through 16 represent calculated sensitivity maps obtained with the 2D model for all the methods studied. Other measurements not shown are redundant ones in terms of the sensitivity maps in homogeneous circular models. The field is only rotated and/or mirrored due to the homogeneity and symmetry of the model. Black electrode locations are used for current delivery and red ones for voltage detection. The sensitivity is shown in the colorbar, positive values indicated with brighter, negative with darker color. Scaling of the colormap is kept the same within each animation, null sensitivity lines are shown with black lines. Animations. Adaptive method
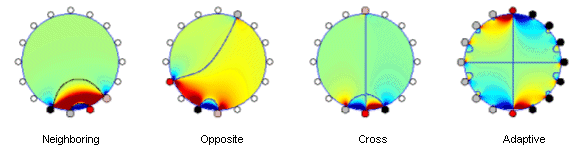
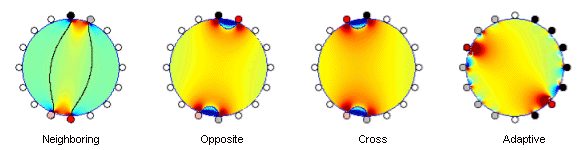
Relatively large regions of negative sensitivity can be seen in all animations. Example individual sensitivity distributions having regions of both positive and negative sensitivities simultaneously are given in Fig. 3 for each method. Sensitivity distributions being the most sensitive to detect the centre region for each of the studied methods are illustrated in Fig. 4, the most selective configurations in Fig. 5. Figure 3. Selected sensitivity distributions showing regions of positive and negative sensitivities for all the methods as simulated in 2D homogeneous model. Figure 4. The most sensitive configurations to detect centre region of the model. |
| IJBEM, 2006, Vol. 8, No. 1 | Page VII/7 |
|
Figure 5. Most selective configurations for each method. Figure 6 depicts the potential field (note, not sensitivity distribution) due to trigonometric current injection pattern of the adaptive method in each of the models used in the study. For the 2D disk model, the field is highly homogeneous as expected, whereas in the 3D case, the field spreads more causing inhomogeneous current field. When including the realistic 2D head boundary and inhomogeneities within the head, the field is even more inhomogeneous as compared to the radially symmetrical cases. In Anim. 17 the trigonometric current injection is rotated 360 degrees around the thorax. Figure 6. Potential fiels due to trigonometric current injection in different models used in the study. Animation.
4. Discussion The purpose of the study was to emphasize the importance of the sensitivity field and to demonstrate that the lead field approach is suitable in investigating EIT. Several measurement configurations simulated in simplified homogeneous cases were visualized and animated in respect of their measurement sensitivity distributions. Previous work has applied the forward solution mainly in developing reconstruction algorithms, for example Liston et al derived sensitivity matrixes on multi shell models (Liston et al 2002). They, however, did not investigate the form of the sensitivity field; instead they visualized the current field. It should be noted, that the actual measurement sensitivity is not illustrated with current field, but by the dot product field of the current injection and the voltage measurement lead fields. In another study, sensitivity was investigated in a physical tank model (Jossinet and Kardous 1987). It was found, that sensitivity was often higher close to the electrodes, but no clear indication of negative sensitivity was reported. The anticipated results in our study revealed that often most of the measurement sensitivity is concentrated in regions close to the surface and that a considerable region of negative sensitivity lay often near the electrodes. Close to the electrodes the sensitivity field has large gradients, i.e. the high positive sensitivity (large contribution) may change in a few millimetres to high negative sensitivity having opposite contribution to the measured value. Negative sensitivity as depicted by Eq. 1 is detected in regions where the two lead fields have opposite components. |
| IJBEM, 2006, Vol. 8, No. 1 | Page VII/8 |
|
The neighboring method was the least sensitive in the centre as compared to the others. However, its proportional selectivity was the best. Actual sensitivity value might not always be as important as the selectivity. The most sensitive (although not necessarily the most selective one at the same time) method may be used when the approximate location of expected impedance change is known. Then the change in detected signal is the largest. Whereas, when the relative contribution from certain region is more important than the signal level (when seeking the location of the change), the most selective configuration yields more favourable results. Between the opposite, cross and the adaptive methods the values did not vary largely. As expected, the adaptive method produced most homogeneous sensitivity throughout the model. The adaptive current injection was visualized separately (Fig. 6 and Anim. 17). For the 2D slice, the generated field is homogeneous, whereas in the 3D model the currents are not strictly confined to a cross section, but spread in 3D. In the 2D head model the internal inhomogeneities and the shape of the outer boundary clearly modify the field making it more inhomogeneous. Also, rotating the current feed around the head modifies the resulted field. For the adaptive method, no optimization of the current injection patterns was used, which would have been likely to increase the sensitivity and selectivity of the measurement. A further application of EIT could evolve in providing regional conductivity for use in solving the inverse problem of ECG (Newell 1985) or EEG (Goncalves et al 2000). Regional conductivity and its changes detected by impedance might provide an initial estimation whether the subject is suffering from brain ischemia or hemorrhage, which require the use of either thrombolytic or antithrombotic drugs having quite the opposite actions. The measurement could quite simply be integrated into a portable emergency EEG device and used simultaneously with the EEG recording by the paramedics prior entering a hospital. This application is presently under investigation by our group. The results of the present study are only illustrative and the purpose was to demonstrate the application of the lead field approach in analyzing the EIT measurements. The models used were therefore simple, linear and no realistic electrode model was used. Based on our results, no obvious indication of the preference of any acquisition method may be given. In reality, the fields are much more complex than in our simplified linear cases. An indication of complexity was obtained with the 2D realistic model, showing clear deviations from the symmetrical models. Noise level and the implementation of EIT instrumentation and inverse solution have their own impact and restrictions on the data acquisition method. However, the analysis can be extended to more sophisticated models, with additional focus on the derivation of optimal excitation and measurement configurations in realistic geometry and conductivity distributions and in the existence of noise. As the sensitivity is low in deeper regions resulting to low resolution, it is feasible to seek measurement combinations that would improve the method in that aspect. Employing multiple measurements with different and known sensitivities to the relevant region may convey useful information related to some specific event or region undetectable by conventional measurement strategies. The human tissues are not strictly conductive and the assumption of the linearity does not hold completely. Whether one should concentrate on finding the most selective or sensitive measurements in the inner regions by off-line derivation from independent data or by actual direct measurements utilizing more than four electrodes at a time, remains to be investigated. Acknowledgements This work was supported financially by the Ragnar Granit Foundation. www.rgs.fi References Bourne J R (ed.). Bioelectrical impedance techniques in medicine. Critical Reviews in Biomedical Engineering,24 (issues 4-6), 1996. Brown B H. Overview of clinical applications. In proc of the Copenhagen Meeting on Electrical Impedance Tomography 29-35, 1990. Brown B H, Segar A D. The Sheffield data collection system. Clinical Physics and Physiological Measurement, 8 Suppl A:91-97, 1987. Geselowitz D B. An application of electrocardiographic lead theory to impedance plethysmography. IEEE Transactions on Biomedical Engineering, 18: 38-41, 1971. Goncalves S, de Munck J C, Heethaar R M, Lopes da Silva F H and van Dijk B W. The application of electrical impedance tomography to reduce systematic errors in the EEG inverse problem - a simulation study. Physiological Measurement, 21: 379-93, 2000. Grimnes S, Martinsen O G. Bioimpedance & Bioelectricity Basics. Academic Press, London, 2000. Hua P, Webster J G, Tompkins W J. Effect of the measurement method on noise handling and image quality of EIT imaging. In proceedings of the 9th International Conference of the IEEE Engineering in Medicine and Biology Society, 1987, 1429-1430. Holder D (ed.). Electrical Impedance Tomography - Methods, history and Applications. Institute of Physics Publishing, Bristol, 2005.x Jossinet J, Kardous G. Physical study of the sensitivity distribution in multi-electrode systems. Clinical Physics and Physiological Measurement,8 Suppl A:33-7, 1987. |
| IJBEM, 2006, Vol. 8, No. 1 | Page VII/9 |
|
Kauppinen P K, Hyttinen J A, Heinonen T and Malmivuo J. A detailed model of the thorax as a volume conductor based on the visible human man data. Journal of Medical Engineering and Technologyx, 22: 126-133, 1998. Kauppinen P, Koobi T, Kaukinen S, Hyttinen J and Malmivuo J. Application of computer modelling and lead field theory in developing multiple aimed impedance cardiography measurements. Journal of Medical Engineering and Technology, 23: 169-177, 1999. Kauppinen P, Hyttinen J, Laarne P, Malmivuo J. A software implementation for detailed volume conductor modelling in electrophysiology using finite difference method. Computer Methods and Programs in Biomedicine, 58: 191-203, 1999b. Kauppinen P, Hyttinen J, Malmivuo J. Sensitivity distribution simulations of impedance tomography electrode combinations. International Journal of Bioelectromagnetism, 7(1): 344-347, 2005. Liston A D, Bayford R H, Tidswell A T and Holder D S. A multi-shell algorithm to reconstruct EIT images of brain function. Physiological Measurement, 23 105-19, 2002. Malmivuo J, Plonsey R. Bioelectromagnetism: Principles and Application of Bioelectric and Biomagnetic Fields. Oxford University Press, New York, 1995. www.bem.fi/book/ Newell J C. State of the art in impedance imaging. In proc of the IX International Conference on Electrical Bio-Impedance, 9-12, 1995. Zhu Q, Lionheart W R, Lidgey F J, McLeod C N, Paulson K S and Pidcock M K. An adaptive current tomography using voltage sources. IEEE Transactions on Biomedical Engineering, 40: 163-8, 1993.
|