7.1 CONCEPTS OF VOLUME SOURCE AND VOLUME CONDUCTOR
The field of science and engineering most relevant to electrophysiology and bioelectromagnetism is electrical engineering. However, the electrical engineering student will quickly note some important distinctions in emphasis between these disciplines. Much of electrical engineering deals with networks made up of batteries, resistances, capacitances, and inductors. Each of these elements, while actually comprising a physical object, is considered to be discrete. Electric circuits and electric networks have been extensively studied to elucidate the properties of their structures. In electrophysiology and bioelectromagnetism there are no inductors, while resistances, capacitances, and batteries are not discrete but distributed. That is, the conducting medium extends continuously; it is three-dimensional and referred to as a volume conductor. Although the capacitance is localized to cellular membranes, since normally our interest is in multicellular preparations (e.g., brain tissue or cardiac muscle) which extend continuously throughout a three-dimensional region, the capacitance must also be deemed to be distributed. In fact, this is true as well for the "batteries," which are also continuously distributed throughout these same membranes.
In electrophysiology and bioelectromagnetism there are no inductors, while resistances, capacitances, and batteries are not discrete but distributed. That is, the conducting medium extends continuously; it is three-dimensional and referred to as a volume conductor. Although the capacitance is localized to cellular membranes, since normally our interest is in multicellular preparations (e.g., brain tissue or cardiac muscle) which extend continuously throughout a three-dimensional region, the capacitance must also be deemed to be distributed. In fact, this is true as well for the "batteries," which are also continuously distributed throughout these same membranes.
 Although the classical studies in electricity and magnetism are relevant, it is the area of electromagnetic fields that is the most pertinent. Such application to volume conductors is discussed later in detail in Chapter 11, where it is shown that they form an independent and logical discipline. Wherever possible, results from the simple sources discussed in the earlier chapters will be applied under more realistic conditions.
Although the classical studies in electricity and magnetism are relevant, it is the area of electromagnetic fields that is the most pertinent. Such application to volume conductors is discussed later in detail in Chapter 11, where it is shown that they form an independent and logical discipline. Wherever possible, results from the simple sources discussed in the earlier chapters will be applied under more realistic conditions.
 A major object of this chapter is to introduce the bioelectric sources and the electric fields arising from the sources. Another important task is to discuss the concept of modeling. It is exemplified by modeling the bioelectric volume sources, like those within the entire heart, and volume conductors, like the entire human body. This chapter provides also a preliminary discussion of the fundamental problems concerning the bioelectric or biomagnetic fields arising from the sources, called the solutions to the forward problem, and the general preconditions for the determination of the sources giving a description of the field, called the solutions to the inverse problem. The discussion on bioelectric sources and the fields that they produce is continued on a theoretical basis in Chapter 8.
A major object of this chapter is to introduce the bioelectric sources and the electric fields arising from the sources. Another important task is to discuss the concept of modeling. It is exemplified by modeling the bioelectric volume sources, like those within the entire heart, and volume conductors, like the entire human body. This chapter provides also a preliminary discussion of the fundamental problems concerning the bioelectric or biomagnetic fields arising from the sources, called the solutions to the forward problem, and the general preconditions for the determination of the sources giving a description of the field, called the solutions to the inverse problem. The discussion on bioelectric sources and the fields that they produce is continued on a theoretical basis in Chapter 8.
7.2 BIOELECTRIC SOURCE AND ITS ELECTRIC FIELD
7.2.1 Definition of the Preconditions
The discussions in each section that follows are valid under a certain set of conditions - that is, for certain types of electric sources within certain types of volume conductors. Therefore, some limiting assumptions, or preconditions, are given first. One should note that when the preconditions are more stringent than the actual conditions the discussion will necessarily be valid. For instance, if the preconditions indicate the discussion is valid in an infinite homogeneous volume conductor, then it is not valid in a finite inhomogeneous volume conductor. On the other hand, if the preconditions indicate the discussion is valid in a finite inhomogeneous volume conductor, then it is also valid in a finite homogeneous volume conductor because the latter is a special case of the former. It should be noted that all volume conductors are assumed to be linear (consistent with all experimental evidence). If the volume conductor is presumed to be homogeneous, it is assumed to be isotropic as well. The various types of sources and conductors are characterized later in this chapter.
It should be noted that all volume conductors are assumed to be linear (consistent with all experimental evidence). If the volume conductor is presumed to be homogeneous, it is assumed to be isotropic as well. The various types of sources and conductors are characterized later in this chapter.
7.2.2 Volume Source in a Homogeneous Volume Conductor
PRECONDITIONS:SOURCE: Volume source
CONDUCTOR: Infinite, homogeneous
Let us introduce the concept of the impressed current density  i(x,y,z,t). This is a nonconservative current, that arises from the bioelectric activity of nerve and muscle cells due to the conversion of energy from chemical to electric form. The individual elements of this bioelectric source behave as electric current dipoles. Hence the impressed current density equals the volume dipole moment density of the source. Note that
i(x,y,z,t). This is a nonconservative current, that arises from the bioelectric activity of nerve and muscle cells due to the conversion of energy from chemical to electric form. The individual elements of this bioelectric source behave as electric current dipoles. Hence the impressed current density equals the volume dipole moment density of the source. Note that  i is zero everywhere outside the region of active cells (Plonsey, 1969). (Note also that bioelectric sources were formerly modeled by dipoles or double layers formed by the component electric charges. Today we think of the current source as the basic element.)
i is zero everywhere outside the region of active cells (Plonsey, 1969). (Note also that bioelectric sources were formerly modeled by dipoles or double layers formed by the component electric charges. Today we think of the current source as the basic element.)
 If the volume conductor is infinite and homogeneous and the conductivity is σ, the primary sources
If the volume conductor is infinite and homogeneous and the conductivity is σ, the primary sources  i establish an electric field
i establish an electric field  and a conduction current σ
and a conduction current σ . As a result, the total current density (Geselowitz, 1967) is given by:
. As a result, the total current density (Geselowitz, 1967) is given by:
 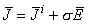 | (7.1) |
The quantity σ is often referred to as the return current. This current is necessary to avoid buildup of charges due to the source current.
is often referred to as the return current. This current is necessary to avoid buildup of charges due to the source current.
 Because the electric field
Because the electric field  is quasistatic (see Section 7.2.4), it can be expressed at each instant of time as the negative gradient of a scalar potential Φ, and Equation 7.1 may be rewritten
is quasistatic (see Section 7.2.4), it can be expressed at each instant of time as the negative gradient of a scalar potential Φ, and Equation 7.1 may be rewritten
 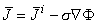 | (7.2) |
 Since the tissue capacitance is negligible (quasistatic conditions), charges redistribute themselves in a negligibly short time in response to any source change. Since the divergence of
Since the tissue capacitance is negligible (quasistatic conditions), charges redistribute themselves in a negligibly short time in response to any source change. Since the divergence of  evaluates the rate of change of the charge density with respect to time, and since the charge density must be zero, the divergence of
evaluates the rate of change of the charge density with respect to time, and since the charge density must be zero, the divergence of  is necessarily zero. (We refer to the total current
is necessarily zero. (We refer to the total current  as being solenoidal, or forming closed lines of current flow.) Therefore, Equation 7.1 reduces to Poisson's equation:
as being solenoidal, or forming closed lines of current flow.) Therefore, Equation 7.1 reduces to Poisson's equation:
 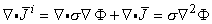 | (7.3) |
Equation 7.3 is a partial differential equation satisfied by σΦ in which 

 i is the source function (or forcing function).
i is the source function (or forcing function).
 The solution of Equation 7.3 for the scalar function σΦ for a region that is uniform and infinite in extent (Stratton, 1941) is:
The solution of Equation 7.3 for the scalar function σΦ for a region that is uniform and infinite in extent (Stratton, 1941) is:
 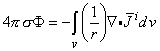 | (7.4) |
Since a source element -

 idv in Equation 7.4 behaves like a point source, in that it sets up a field, that varies as 1/r (as will be explained in more detail later in Equation 8.35), the expression -
idv in Equation 7.4 behaves like a point source, in that it sets up a field, that varies as 1/r (as will be explained in more detail later in Equation 8.35), the expression -

 i is defined as a flow source density (IF). Because we seek the solution for field points outside the region occupied by the volume source, Equation 7.4 may be transformed (Stratton, 1941) to:
i is defined as a flow source density (IF). Because we seek the solution for field points outside the region occupied by the volume source, Equation 7.4 may be transformed (Stratton, 1941) to:
 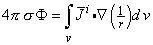 | (7.5) |
This equation represents the distribution of potential ΦF due to the bioelectric source  i within an infinite, homogeneous volume conductor having conductivity σ. Here
i within an infinite, homogeneous volume conductor having conductivity σ. Here  idv behaves like a dipole element (with a field that varies as its dot product with
idv behaves like a dipole element (with a field that varies as its dot product with  (1/r), and hence
(1/r), and hence  i can be interpreted as a volume dipole density).
i can be interpreted as a volume dipole density).
 In this section we started with a formal definition of
In this section we started with a formal definition of  i as an impressed current density (a nonconservative vector field) and developed its role as a source function of potential fields. These are expressed by Equations 7.4 and 7.5. But identical expressions will be obtained in Chapter 8 (namely Equations 8.34 and 8.32) based on an interpretation of
i as an impressed current density (a nonconservative vector field) and developed its role as a source function of potential fields. These are expressed by Equations 7.4 and 7.5. But identical expressions will be obtained in Chapter 8 (namely Equations 8.34 and 8.32) based on an interpretation of  i as a dipole moment per unit volume. This underscores the dual role played by the distribution
i as a dipole moment per unit volume. This underscores the dual role played by the distribution  i, and provides alternative ways in which it can be evaluated from actual experiments. (One such approach will be illustrated in Chapter 8.) These alternate interpretations are, in fact, illustrated by Equations 7.4 and 7.5.
i, and provides alternative ways in which it can be evaluated from actual experiments. (One such approach will be illustrated in Chapter 8.) These alternate interpretations are, in fact, illustrated by Equations 7.4 and 7.5.
7.2.3 Volume Source in an Inhomogeneous Volume Conductor
PRECONDITIONS:SOURCE: Volume source
CONDUCTOR: Inhomogeneous
In Section 7.2.2 it was assumed that the medium is uniform (i.e., infinite and homogeneous). Such an assumption allowed the use of simple expressions that are valid only for uniform homogeneous media of infinite extent. However, even an in vitro preparation that is reasonably homogeneous is nevertheless bounded by air, and hence globally inhomogeneous. One can take such inhomogeneities into account by adding additional terms to the solution. In this section we consider inhomogeneities by approximating the volume conductor by a collection of regions, each one of which is homogeneous, resistive, and isotropic, where the current density  i is linearly related to the electric field intensity
i is linearly related to the electric field intensity  (Schwan and Kay, 1956). We show that such inhomogeneities can be taken into account while at the same time retaining the results obtained in Section 7.2.2 (which were based on the assumption of uniformity).
(Schwan and Kay, 1956). We show that such inhomogeneities can be taken into account while at the same time retaining the results obtained in Section 7.2.2 (which were based on the assumption of uniformity).
 An inhomogeneous volume conductor can be divided into a finite number of homogeneous regions, each with a boundary Sj. On these boundaries both the electric potential Φ and the normal component of the current density must be continuous:
An inhomogeneous volume conductor can be divided into a finite number of homogeneous regions, each with a boundary Sj. On these boundaries both the electric potential Φ and the normal component of the current density must be continuous:
 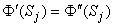 | (7.6) |
 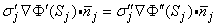 | (7.7) |
where the primed and double-primed notations represent the opposite sides of the boundary and  j is directed from the primed region to the double-primed one.
j is directed from the primed region to the double-primed one.
 If dv is a volume element, and Ψ and Φ are two scalar functions that are mathematically well behaved in each (homogeneous) region, it follows from Green's theorem (Smythe, 1968) that
If dv is a volume element, and Ψ and Φ are two scalar functions that are mathematically well behaved in each (homogeneous) region, it follows from Green's theorem (Smythe, 1968) that
 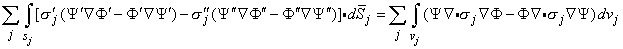 | (7.8) |
If we make the choice of Ψ = 1/r, where r is the distance from an arbitrary field point to the element of volume or area in the integration, and Φ is the electric potential, and substitute Equations 7.3, 7.6, and 7.7 into Equation 7.8, then we obtain the following useful result (Geselowitz, 1967):
 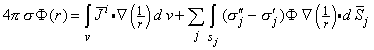 | (7.9) |
This equation evaluates the electric potential anywhere within an inhomogeneous volume conductor containing internal volume sources.
 The first term on the right-hand side of Equation 7.9 involving
The first term on the right-hand side of Equation 7.9 involving  i corresponds exactly to Equation 7.5 and thus represents the contribution of the volume source. The effect of inhomogeneities is reflected in the second integral, where (σj" - σj' )Φ
i corresponds exactly to Equation 7.5 and thus represents the contribution of the volume source. The effect of inhomogeneities is reflected in the second integral, where (σj" - σj' )Φ j is an equivalent double layer source (
j is an equivalent double layer source ( j is in the direction of d
j is in the direction of d j ). The double layer direction, that of
j ). The double layer direction, that of  j or d
j or d j, is the outward surface normal (from the prime to double-prime region). This can be emphasized by rewriting Equation 7.9 as
j, is the outward surface normal (from the prime to double-prime region). This can be emphasized by rewriting Equation 7.9 as
 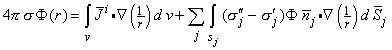 | (7.10) |
 Note that the expression for the field from
Note that the expression for the field from  i (involving
i (involving  (1/r)) is in exactly the same form as (σj" - σj' ) Φ
(1/r)) is in exactly the same form as (σj" - σj' ) Φ j, except that the former is a volume source density (volume integral) and the latter a surface source density (surface integral). In Equations 7.9 and 7.10, and previous equations, the gradient operator is expressed with respect to the source coordinates whereupon
j, except that the former is a volume source density (volume integral) and the latter a surface source density (surface integral). In Equations 7.9 and 7.10, and previous equations, the gradient operator is expressed with respect to the source coordinates whereupon  (1/r) =
(1/r) =  r /r 2 and
r /r 2 and  r is from the source to field. The volume source
r is from the source to field. The volume source  i is the primary source, whereas the surface sources that are invoked by the field established by the primary source (therefore secondary to that source) are referred to as secondary sources.
i is the primary source, whereas the surface sources that are invoked by the field established by the primary source (therefore secondary to that source) are referred to as secondary sources.
 We want to point out once again that the first term on the right-hand side of Equation 7.9 describes the contribution of the volume source, and the second term the contribution of boundaries separating regions of different conductivity - that is, the contribution of the inhomogeneities within the volume conductor. This may be exemplified as follows: If the conductivity is the same on both sides of each boundary Sj - that is, if the volume conductor is homogeneous - the difference (σ"j - σ'j) on each boundary Sj in the second term is zero, and Equation 7.9 (applicable in an inhomogeneous volume conductor) reduces to Equation 7.5 (applicable in a homogeneous volume conductor).
We want to point out once again that the first term on the right-hand side of Equation 7.9 describes the contribution of the volume source, and the second term the contribution of boundaries separating regions of different conductivity - that is, the contribution of the inhomogeneities within the volume conductor. This may be exemplified as follows: If the conductivity is the same on both sides of each boundary Sj - that is, if the volume conductor is homogeneous - the difference (σ"j - σ'j) on each boundary Sj in the second term is zero, and Equation 7.9 (applicable in an inhomogeneous volume conductor) reduces to Equation 7.5 (applicable in a homogeneous volume conductor).
 The purpose of measuring bioelectric signals is to measure their source, not the properties of the volume conductor with the aid of the source inside it. Therefore, the clinical measurement systems of bioelectric events should be designed so that the contribution of the second term in Equation 7.9 is as small as possible. Later, Chapter 11 introduces various methods for minimizing the effect of this term.
The purpose of measuring bioelectric signals is to measure their source, not the properties of the volume conductor with the aid of the source inside it. Therefore, the clinical measurement systems of bioelectric events should be designed so that the contribution of the second term in Equation 7.9 is as small as possible. Later, Chapter 11 introduces various methods for minimizing the effect of this term.
 Equation 7.9 includes a special case of interest in which the preparation of interest (e.g., the human body) lies in air, whereupon σ"j = 0 corresponding to the bounding nonconducting space.
Equation 7.9 includes a special case of interest in which the preparation of interest (e.g., the human body) lies in air, whereupon σ"j = 0 corresponding to the bounding nonconducting space.
7.2.4 Quasistatic Conditions
In the description of the volume conductor constituted by the human body, the capacitive component of tissue impedance is negligible in the frequency band of internal bioelectric events, according to the experimental evidence of Schwan and Kay (1957). They showed that the volume conductor currents were essentially conduction currents and required only specification of the tissue resistivity. The electromagnetic propagation effect can also be neglected (Geselowitz, 1963). This condition implies that time-varying bioelectric currents and voltages in the human body can be examined in the conventional quasistatic limit (Plonsey and Heppner, 1967). That is, all currents and fields behave, at any instant, as if they were stationary. The description of the fields resulting from applied current sources is based on the understanding that the medium is resistive only, and that the phase of the time variation can be ignored (i.e., all fields vary synchronously).
This condition implies that time-varying bioelectric currents and voltages in the human body can be examined in the conventional quasistatic limit (Plonsey and Heppner, 1967). That is, all currents and fields behave, at any instant, as if they were stationary. The description of the fields resulting from applied current sources is based on the understanding that the medium is resistive only, and that the phase of the time variation can be ignored (i.e., all fields vary synchronously).
7.3 THE CONCEPT OF MODELING
7.3.1 The purpose of modeling
A practical way to investigate the function of living organisms is to construct a model that follows the operation of the organism as accurately as possible. The model may be considered to represent a hypothesis regarding physiological observations. Often the hypothesis features complicated interactions between several variables, whose mutual dependence is difficult to determine experimentally. The behavior of the model should be controlled by the basic laws of science (e.g., Ohm's law, Kirchhof's law, thermodynamic laws, etc.). The purpose of the model is to facilitate deduction and to be a manipulative representation of the hypothesis. It is possible to perform experiments with the model that are not possible with living tissues; these may yield outputs based on assumed structural parameters and various inputs (including, possibly, noise). One can better understand the real phenomenon by comparing the model performance to experimental results. The model itself may also be improved in this way. A hypothesis cannot be accepted before it has been sufficiently analyzed and proven in detail.
The purpose of the model is to facilitate deduction and to be a manipulative representation of the hypothesis. It is possible to perform experiments with the model that are not possible with living tissues; these may yield outputs based on assumed structural parameters and various inputs (including, possibly, noise). One can better understand the real phenomenon by comparing the model performance to experimental results. The model itself may also be improved in this way. A hypothesis cannot be accepted before it has been sufficiently analyzed and proven in detail.
 Models have been criticized. For instance, it is claimed that models, which are not primary by construction, cannot add new information to the biological phenomenon they represent. In other words, models do not have scientific merit. We should note, however, that all of our concepts of our surroundings are based on models. Our perception is limited both methodically and conceptually. If we should abandon all "models of models," we would have to relinquish, for example, all the electric heart models in the following chapters of this textbook. They have been the basis for meritorious research in theoretical electrocardiology, which has been essential for developing clinical electrocardiology to its present status. Similarly, the electronic neuron models, which will be briefly reviewed in Chapter 10, serve as an essential bridge from neurophysiology to neurocomputers. Neurocomputers are a fascinating new field of computer science with a wide variety of important applications.
Models have been criticized. For instance, it is claimed that models, which are not primary by construction, cannot add new information to the biological phenomenon they represent. In other words, models do not have scientific merit. We should note, however, that all of our concepts of our surroundings are based on models. Our perception is limited both methodically and conceptually. If we should abandon all "models of models," we would have to relinquish, for example, all the electric heart models in the following chapters of this textbook. They have been the basis for meritorious research in theoretical electrocardiology, which has been essential for developing clinical electrocardiology to its present status. Similarly, the electronic neuron models, which will be briefly reviewed in Chapter 10, serve as an essential bridge from neurophysiology to neurocomputers. Neurocomputers are a fascinating new field of computer science with a wide variety of important applications.
 In addition to the analysis of the structure and function of organic nature, one should include synthesis as an important method - that is, the investigation of organic nature by model construction.
In addition to the analysis of the structure and function of organic nature, one should include synthesis as an important method - that is, the investigation of organic nature by model construction.
7.3.2 Basic Models of the Volume Source
Let us now consider some basic volume source models and their corresponding number of undetermined coefficients or degrees of freedom. (The reader should be aware, that there are a large number of other models available, which are not discussed here.) These are:Dipole
The (fixed-) dipole model is based on a single dipole with fixed location and variable orientation and magnitude. This model has three independent variables: the magnitudes of its three components x, y, and z in Cartesian coordinates (or the dipole magnitude and two direction angles, M, θ, and ϕ, in the spherical coordinates).Moving Dipole
The moving-dipole model is a single dipole that has varying magnitude and orientation, like the fixed dipole, and additionally variable location. Therefore, it has six independent variables.Multiple Dipole
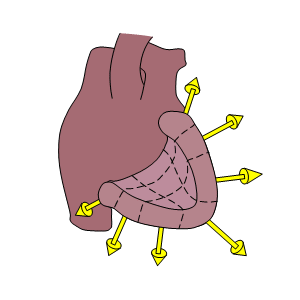
The multiple-dipole model includes several dipoles, each representing a certain anatomical region of the heart. These dipoles are fixed in location and have varying magnitude and varying orientation. If also the orientation is fixed, each dipole has only one independent variable, the magnitude. Then the number of independent variables is equal to the number of the dipoles.Multipole
Just as the dipole is formed from two equal and opposite monopoles placed close together, a quadrupole is formed from two equal and opposite dipoles that are close together. One can form higher-order source configurations by continuing in this way (the next being the octapole, etc.). Each such source constitutes a multipole. What is important about multipoles is that it can be shown that any given source configuration can be expressed as an infinite sum of multipoles of increasing order (i.e., dipole, quadrupole, octapole, etc.). The size of each component multipole depends on the particular source distribution. Each multipole component, in turn, is defined by a number of coefficients. For example, we have already seen that the dipole is described by three coefficients (which can be identified as the strength of its x, y, and z components). It turns out that the quadrupole has five coefficients - the octapole seven, and so on. The multipole may be illustrated in different ways. One of them is the spherical harmonic multipoles, which is given in Figure 7.1. A summary of these source models and the number of their independent variables are presented in Table 7.1, and the structure of the models is schematically illustrated in Figure 7.2.
A summary of these source models and the number of their independent variables are presented in Table 7.1, and the structure of the models is schematically illustrated in Figure 7.2.
number of their independent variables
| Model | Number of variables |
|
Dipole Moving dipole Multiple dipole Multipole Dipole Quadrupole Octapole |
3 6 n,(3n)*
3 |
3n for dipoles with variable orientation.
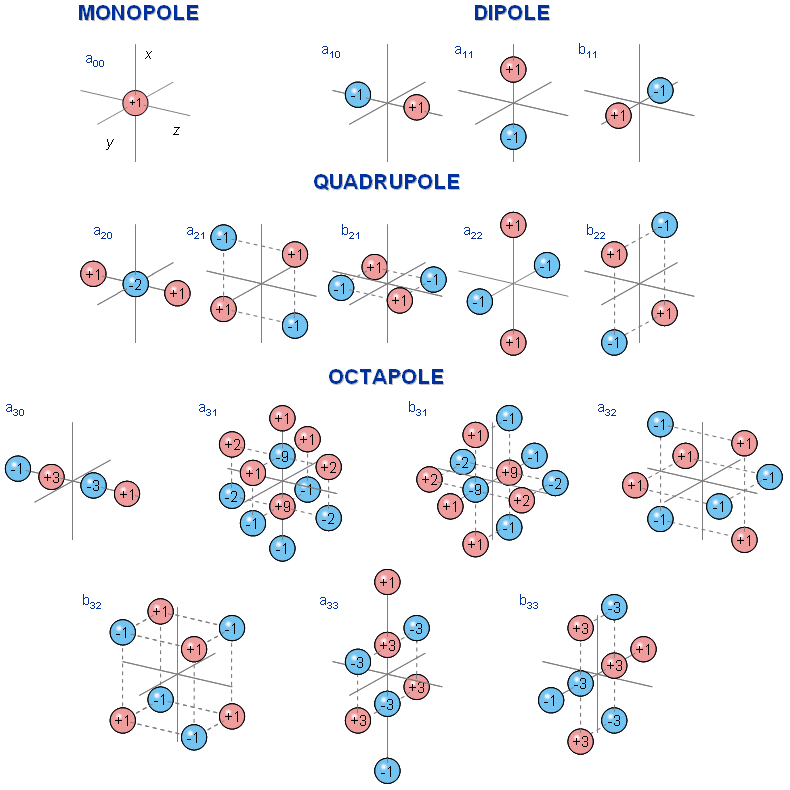
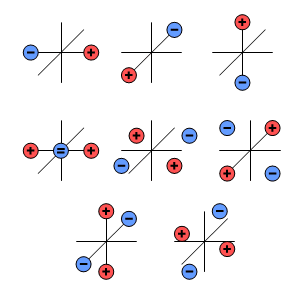
Fig. 7.1. Source-sink illustration of spherical harmonic multipole components (Wikswo and Swinney, 1984). The figure shows the physical source-sink configurations corresponding to the multipole components of the dipole (three components), quadrupole (five components), and octapole (seven components).
 |  | ||
|
| ||
 |  | ||
|
|
- Fig. 7.2. Models used for representing the volume source.
7.3.3 Basic Models of the Volume Conductor
The volume conductor can be modeled in one of the following ways, which are classified in order of increasing complexity:Infinite, Homogenous
The homogeneous model of the volume conductor with an infinite extent is a trivial case, which completely ignores the effects of the conductor boundary and internal inhomogeneities.Finite, Homogenous
Spherical. In its most simple form the finite homogeneous model is a spherical model (with the source at its center). It turns out that for a dipole source the field at the surface has the same form as in the infinite homogeneous volume conductor at the same radius except that its magnitude is three times greater. Therefore, this can also be considered a trivial case.Realistic Shape, Homogeneous. The finite or bounded homogeneous volume conductor with real shape takes into consideration the actual outer boundary of the conductor (the thorax, the head, etc.) but ignores internal inhomogeneities.
Finite, Inhomogeneous
The finite inhomogeneous model takes into consideration the finite dimensions of the conductor and one or more of the following internal inhomogeneities.
Torso.
 Cardiac muscle tissue
Cardiac muscle tissue
 High-conductivity intracardiac blood mass
High-conductivity intracardiac blood mass
 Low-conductivity lung tissue
Low-conductivity lung tissue
 Surface muscle layer
Surface muscle layer
 Nonconducting bones such as the spine and the sternum
Nonconducting bones such as the spine and the sternum
 Other organs such as the great vessels, the liver, etc.
Other organs such as the great vessels, the liver, etc.
Head.
 The specific conducting regions that are ordinarily identified for the head as a volume conductor are:
The specific conducting regions that are ordinarily identified for the head as a volume conductor are:
 Brain
Brain
 Cerebrospinal fluid
Cerebrospinal fluid
 Skull
Skull
 Muscles
Muscles
 Scalp
Scalp
 The volume conductor models are summarized in Table 7.2. The resistivities of various tissues are given in Table 7.3.
The volume conductor models are summarized in Table 7.2. The resistivities of various tissues are given in Table 7.3.
| Model | Properties | |
| Infinite homogeneous
b. Realistic shape Finite inhomogeneous |
the trivial case; does not consider the volume conductor's electric properties or its boundary with air
another trivial case if |
|
7.4 THE HUMAN BODY AS A VOLUME CONDUCTOR
7.4.1 Tissue Resistivities
The human body may be considered as a resistive, piecewise homogeneous and linear volume conductor. Most of the tissue is isotropic. The muscle is, however, strongly anisotropic, and the brain tissue is anisotropic as well. Figure 7.3 illustrates the cross section of the thorax, and Table 7.3 summarizes the tissue resistivity values of a number of components of the human body. More comprehensive lists of tissue resistivities are given in Geddes and Baker (1967), Barber and Brown (1984), and Stuchly and Stuchly (1984).
| Tissue | ρ[Ώm] | Remarks | Reference |
| Brain
Skeletal muscle
Liver
Fat |
2.2 6.8 5.8 0.7 1.6 0.7 2.5 5.6 1.9 13.2 7 11.2 21.7 25 177 15 158 215 |
gray matter white matter average Hct = 45
longitudinal
longitudinal |
Rush and Driscoll, 1969 Barber and Brown, 1984 " Barber and Brown, 1984 Geddes and Sadler, 1973 Barber and Brown, 1984 Rush, Abildskov, and McFee, 1963 Epstein and Foster, 1982
Rush, Abildskov, and McFee, 1963 |
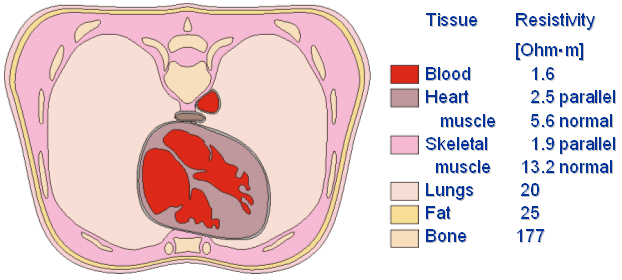
Fig. 7.3. Cross section of the thorax. The resistivity values are given for six different types of tissues.
The resistivity of blood depends strongly on the hematocrit, Hct (which denotes the percent volume of the red blood cells in whole blood) (Geddes and Sadler, 1973). This dependence has an exponential nature and is given in Equation 7.11:
 ρ = 0.537 e0.025Hct ρ = 0.537 e0.025Hct | (7.11) |
 Hugo Fricke studied theoretically the electric conductivity of a suspension of spheroids (Fricke, 1924). When applying this method to the conductivity of blood, we obtain what is called the Maxwell-Fricke equation:
Hugo Fricke studied theoretically the electric conductivity of a suspension of spheroids (Fricke, 1924). When applying this method to the conductivity of blood, we obtain what is called the Maxwell-Fricke equation:
 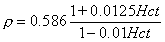 | (7.12) |
| where | ρ | = resistivity of blood [Ωm] |
| Hct | = hematocrit [%] |
 Both of these equations give very accurate values. The correlation coefficient of Equation 7.11 to empirical measurements is r = 0.989. Because the best fitting curve to the measured resistivity values is slightly nonlinear in a semilogarithmic plot, Equation 7.12 gives better values with very low or very high hematocrit values. The resistivity of blood is also a function of the movement of the blood (Liebman, Pearl, and Bagnol, 1962; Tanaka et al., 1970). This effect is often neglected in practice. Equations 7.11 and 7.12 are presented in Figure 7.4..
Both of these equations give very accurate values. The correlation coefficient of Equation 7.11 to empirical measurements is r = 0.989. Because the best fitting curve to the measured resistivity values is slightly nonlinear in a semilogarithmic plot, Equation 7.12 gives better values with very low or very high hematocrit values. The resistivity of blood is also a function of the movement of the blood (Liebman, Pearl, and Bagnol, 1962; Tanaka et al., 1970). This effect is often neglected in practice. Equations 7.11 and 7.12 are presented in Figure 7.4..
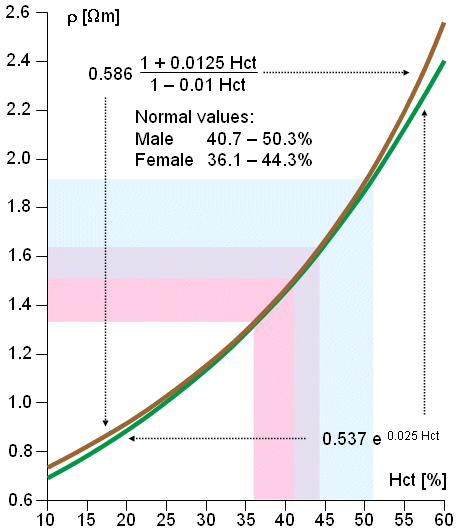
Fig. 7.4. Resistivity of blood as a function of hematocrit (Hct). Equations 7.11 and 7.12 are depicted in graphical form.
7.4.2 Modeling the Head
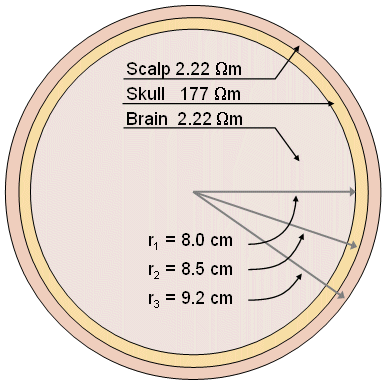
The brain is composed of excitable neural tissue, the study of which is of great interest in view of the vital role played by this organ in human function. Its electric activity, readily measured at the scalp, is denoted the electroencephalogram (EEG). Brain tissue not only is the location of electric sources (generators), but also constitutes part of the volume conductor which includes also the skull and scalp. Regarding volume conductor models, the head has been successfully considered to be a series of concentric spherical regions (the aforementioned brain, skull, and scalp), as illustrated in Figure 7.5 (Rush and Driscoll, 1969). In this model, the inner and outer radii of the skull are chosen to be 8 and 8.5 cm, respectively, while the radius of the head is 9.2 cm. For the brain and the scalp a resistivity of 2.22 Ωm is selected, whereas for the skull a resistivity of 80 × 2.22 Ωm = 177 Ωm is assigned. These numerical values are given solely to indicate typical (mean) physiological quantities. Because of the symmetry, and simplicity, this model is easy to construct as either an electrolytic tank model or a mathematical and computer model. It is also easy to perform calculations with a spherical geometry. Though this simple model does not consider the anisotrophy and inhomogeneity of the brain tissue and the cortical bone (Saha and Williams, 1992), it gives results that correspond reasonably well to measurements.
Regarding volume conductor models, the head has been successfully considered to be a series of concentric spherical regions (the aforementioned brain, skull, and scalp), as illustrated in Figure 7.5 (Rush and Driscoll, 1969). In this model, the inner and outer radii of the skull are chosen to be 8 and 8.5 cm, respectively, while the radius of the head is 9.2 cm. For the brain and the scalp a resistivity of 2.22 Ωm is selected, whereas for the skull a resistivity of 80 × 2.22 Ωm = 177 Ωm is assigned. These numerical values are given solely to indicate typical (mean) physiological quantities. Because of the symmetry, and simplicity, this model is easy to construct as either an electrolytic tank model or a mathematical and computer model. It is also easy to perform calculations with a spherical geometry. Though this simple model does not consider the anisotrophy and inhomogeneity of the brain tissue and the cortical bone (Saha and Williams, 1992), it gives results that correspond reasonably well to measurements.
Fig. 7.5. Concentric spherical head model by Rush and Driscoll (1969). The model contains a region for the brain, scalp, and skull, each of which is considered to be homogeneous.
An empirical approach based on the recognition of typical signal patterns that are known to be associated with certain source configurations.
Imposition of physiological constraints is based on the information available on the anatomy and physiology of the active tissue. This imposes strong limitations on the number of available solutions.
Examining the lead-field pattern, from which the sensitivity distribution of the lead and therefore the statistically most probable source configuration can be estimated.
Modeling the source and the volume conductor using simplified models. The source is characterized by only a few degrees of freedom (for instance a single dipole which can be completely determined by three independent measurements).
We discuss these approaches in more detail in the following:
A model is constructed for the signal source. The model should have a limited number of independent variables yet still have good correspondence with the physiology and anatomy associated with the actual source distribution.
A model is constructed for the volume conductor. The accuracy of the conductor model must be as good as or better than that of the source model.
At least as many independent measurements are made as the model has independent variables. Now we have as many equations as we have unknowns, and the variables of the model can be evaluated.
Barber DC, Brown BH (1984): Applied potential tomography. J. Phys. E.: Sci. Instrum. 17: 723-33.
Epstein BR, Foster KR (1983): Anisotropy as a dielectric property of skeletal muscle. Med. & Biol. Eng. & Comput. 21:(1) 51-5.
Fricke H (1924): A mathematical treatment of the electric conductivity and capacity of disperse systems. Physiol. Rev. 4: 575-87. (Series 2).
Geddes LA, Baker LE (1967): The specific resistance of biological material - A compendium of data for the biomedical engineering and physiologist. Med. Biol. Eng. 5: 271-93.
Geddes LA, Sadler C (1973): The specific resistance of blood at body temperature. Med. Biol. Eng. 11:(5) 336-9.
Geselowitz DB (1963): The concept of an equivalent cardiac generator. Biomed. Sci. Instrum. 1: 325-30.
Geselowitz DB (1967): On bioelectric potentials in an inhomogeneous volume conductor. Biophys. J. 7:(1) 1-11.
Helmholtz HLF (1853): Ueber einige Gesetze der Vertheilung elektrischer Ströme in körperlichen Leitern mit Anwendung auf die thierisch-elektrischen Versuche. Ann. Physik und Chemie 89: 211-33, 354-77.
Horácek BM (1974): Numerical model of an inhomogeneous human torso. In Advances in Cardiology, Vol. 10, ed. S Rush, E Lepeshkin, pp. 51-7, S. Karger, Basel.
Hyttinen JA, Eskola HJ, Sievänen H, Malmivuo JA (1988): Atlas of the sensitivity distribution of the common ECG-lead systems. Tampere Univ. Techn., Inst. Biomed. Eng., Reports 2:(2) 25+67.
Liebman FM, Pearl J, Bagnol S (1962): The electrical conductance properties of blood in motion. Phys. Med. Biol. 7: 177-94.
Macfarlane PW, Lawrie TDV (1974): An Introduction to Automated Electrocardiogram Interpretation, 115 pp. Butterworths, London.
Malmivuo JA (1976): On the detection of the magnetic heart vector - An application of the reciprocity theorem. Helsinki Univ. Tech., Acta Polytechn. Scand., El. Eng. Series. Vol. 39., pp. 112. (Dr. tech. thesis)
McFee R, Baule GM (1972): Research in electrocardiography and magnetocardiography. Proc. IEEE 60:(3) 290-321.
Pilkington TC, Plonsey R (1982): Engineering Contributions to Biophysical Electrocardiography, 248 pp. IEEE Press, John Wiley, New York.
Plonsey R (1969): Bioelectric Phenomena, 380 pp. McGraw-Hill, New York.
Plonsey R, Heppner DB (1967): Considerations of quasistationarity in electrophysiological systems. Bull. Math. Biophys. 29:(4) 657-64.
Rudy Y, Plonsey R (1979): The eccentric spheres model as the basis of a study of the role of geometry and inhomogeneities in electrocardiography. IEEE Trans. Biomed. Eng. BME-26:(7) 392-9.
Rush S (1971): An inhomogeneous anisotropic model of the human torso for electrocardiographic studies. Med. Biol. Eng. 9:(5) 201-11.
Rush S, Abildskov JA, McFee R (1963): Resistivity of body tissues at low frequencies. Circulation 22:(1) 40-50.
Rush S, Driscoll DA (1969): EEG-electrode sensitivity - An application of reciprocity. IEEE Trans. Biomed. Eng. BME-16:(1) 15-22.
Saha S, Williams PA (1992): Electric and dielectric properties of wet human cortical bone as a function of frequency. IEEE Trans. Biomed. Eng. 39:(12) 1298-304.
Schwan HP, Kay CF (1956): Specific resistance of body tissues. Circ. Res. 4:(6) 664-70.
Schwan HP, Kay CF (1957): Capacitive properties of body tissues. Circ. Res. 5:(4) 439-43.
Smythe WR (1968): Static and Dynamic Electricity, 3rd ed., 623 pp. McGraw-Hill, New York.
Stratton JA (1941): Electromagnetic Theory, McGraw-Hill, New York.
Stuchly MA, Stuchly SS (1984): Electrical properties of biological substance. In Biological Effects and Medical Applications of Electromagnetic Fields, ed. OP Gandhi, Academic Press, New York.
Tanaka K, Kanai H, Nakayama K, Ono N (1970): The impedance of blood: The effects of red cell orientation and its application. Jpn. J. Med. Eng. 8: 436-43.
Wikswo JP, Swinney KR (1984): Comparison of scalar multipole expansions. J. Appl. Phys. 56:(11) 3039-49.
7.4.3 Modeling the Thorax
The applied electrophysiological preparation that has generated the greatest interest is that of electrocardiography. The electric sources (generators) lie entirely within the heart, whereas the volume conductor is composed of the heart plus remaining organs in the thorax. Rush, Abildskov, and McFee (1963) introduced two simple models of the thorax. In both, the outer boundary has the shape of a human thorax. In the simpler model, the resistivity of the lungs is selected at 10 Ωm. The intracardiac blood is assigned a resistivity of 1 Ωm. In the more accurate model, the resistivity of the lungs is chosen to be 20 Ωm. In addition, the cardiac muscle and intercostal muscles are modeled with a resistivity of 4 Ωm, and the intracardiac blood is assigned a resistivity of 1.6 Ωm, as described in Figure 7.6. Because the experimentally found tissue resistivity shows a considerable variation, a similarly wide choice of values are used in thorax models.
 In a first-order electrocardiographic (and particularly in a magnetocardiographic) model, the whole heart can be considered to be uniform and spherical. In a second-order model, the left ventricular chamber can be modeled with a sphere of a radius of 5.6 cm and hence a volume of 736 cm3; the cavity is assumed to be filled with blood.
In a first-order electrocardiographic (and particularly in a magnetocardiographic) model, the whole heart can be considered to be uniform and spherical. In a second-order model, the left ventricular chamber can be modeled with a sphere of a radius of 5.6 cm and hence a volume of 736 cm3; the cavity is assumed to be filled with blood.
 In more recent years, several models have been developed which take into account both shape as well as conductivity of the heart, intracavitary blood, pericardium, lungs, surface muscle and fat, and bounding body shape. These include models by Rudy and Plonsey (1979) and Horá ek (1974). A physical inhomogeneous and anisotropic model of the human torso was constructed and described by Rush (1971). This has also been used as the basis for a computer model by Hyttinen et al. (1988).
In more recent years, several models have been developed which take into account both shape as well as conductivity of the heart, intracavitary blood, pericardium, lungs, surface muscle and fat, and bounding body shape. These include models by Rudy and Plonsey (1979) and Horá ek (1974). A physical inhomogeneous and anisotropic model of the human torso was constructed and described by Rush (1971). This has also been used as the basis for a computer model by Hyttinen et al. (1988).
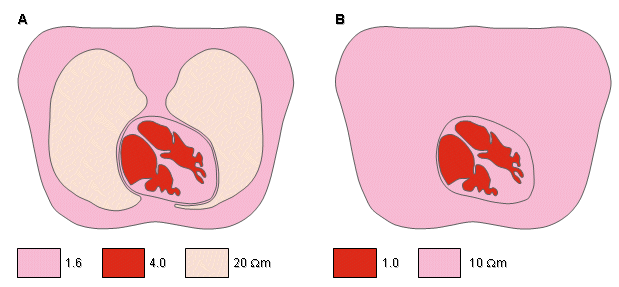
Fig. 7.6. Simplified thorax models by Rush (1971).
(A) Heart, lung, and blood regions are identified.
(B) The lung region is made uniform with the heart and surface muscle.
7.5 FORWARD AND INVERSE PROBLEM
7.5.1 Forward Problem
The problem in which the source and the conducting medium are known but the field is unknown and must be determinated, is called the forward problem. The forward problem has a unique solution. It is always possible to calculate the field with an accuracy that is limited only by the accuracy with which we can describe the source and volume conductor. However, this problem does not arise in clinical (diagnostic) situations, since in this case only the field can be measured (noninvasively) at the body surface.
7.5.2 Inverse Problem
The problem in which the field and the conductor are known but the source is unknown, is called the inverse problem (see Figure 7.7). In medical applications of bioelectric phenomena, it is the inverse problem that has clinical importance. For instance, in everyday clinical diagnosis the cardiologist and the neurologist seek to determine the source of the measured bioelectric or biomagnetic signals. The possible pathology affecting the source provides the basis for their diagnostic decisions - that is, the clinical status of the corresponding organ. What is the feasibility of finding solutions to the inverse problem? This will be discussed in the next section.

Fig. 7.7. Forward and inverse problems.
7.5.3 Solvability of the Inverse Problem
Let us discuss the solvability of the inverse problem with a simplified example of a source and a conductor (Figure 7.8). In this model the source is represented by a single battery, and the conductor by a network of two resistors (McFee and Baule, 1972). Three cases are presented in which the voltage source is placed in different locations within the network and given different values. Note that although the magnitude of the battery voltage is different in each case, the output voltage in all three cases is the same, namely 2 V.
 One may examine each network with Thevenin's theorem (or its dual Norton's theorem), which states that it is always possible to replace a combination of voltage sources and associated circuitry with a single equivalent source and a series impedance. The equivalent emf is the open-circuit voltage, and the series resistance is the impedance looking into the output terminals with the actual sources short-circuited.
One may examine each network with Thevenin's theorem (or its dual Norton's theorem), which states that it is always possible to replace a combination of voltage sources and associated circuitry with a single equivalent source and a series impedance. The equivalent emf is the open-circuit voltage, and the series resistance is the impedance looking into the output terminals with the actual sources short-circuited.
 With this approach, we can evaluate the Thevenin equivalent for the three given circuits. In all cases the equivalent network is the same, namely an emf of 2 V in series with a resistance of 4 Ω. This demonstrates that based on external measurements one can evaluate only the Thevenin network. In this example, we have shown that this network is compatible with (at least) three actual, but different, networks. One cannot distinguish among these different inverse candidates without measurements within the source region itself. The example demonstrates the lack of uniqueness in constructing an inverse solution.
With this approach, we can evaluate the Thevenin equivalent for the three given circuits. In all cases the equivalent network is the same, namely an emf of 2 V in series with a resistance of 4 Ω. This demonstrates that based on external measurements one can evaluate only the Thevenin network. In this example, we have shown that this network is compatible with (at least) three actual, but different, networks. One cannot distinguish among these different inverse candidates without measurements within the source region itself. The example demonstrates the lack of uniqueness in constructing an inverse solution.
 The solvability of the inverse problem was discussed through the use of a simple electronic circuit as an example. The first theoretical paper, which stated that the inverse problem does not have a unique solution, was written by Hermann von Helmholtz (1853)..
The solvability of the inverse problem was discussed through the use of a simple electronic circuit as an example. The first theoretical paper, which stated that the inverse problem does not have a unique solution, was written by Hermann von Helmholtz (1853)..
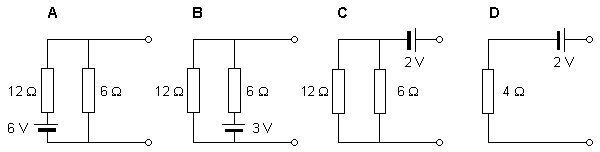
Fig. 7.8. Demonstration of the lack of uniqueness in the inverse problem.
7.5.4 Possible Approaches to the Solution of the Inverse Problem
Cardiac electric activity can be measured on the surface of the thorax as the electrocardiogram. Similarly, the electromyogram, electroencephalogram, and so on, are signals of muscular, neural, and other origins measured noninvasively at the body surface. The question facing the clinician is to determine the electric source (generator) of the measured signal and then to observe whether such source is normal or in what way it is abnormal.
 To find the source, given the measured field, is the statement of the inverse problem. As noted above, a unique solution cannot be found based on external measurements alone. One may therefore ask how it is possible to reach a clinical diagnosis. Despite the discouraging demonstration in the previous section of the theorem regarding the lack of uniqueness of the inverse problem, there are several approaches that overcome this dilemma. Four of these approaches are discussed below:
To find the source, given the measured field, is the statement of the inverse problem. As noted above, a unique solution cannot be found based on external measurements alone. One may therefore ask how it is possible to reach a clinical diagnosis. Despite the discouraging demonstration in the previous section of the theorem regarding the lack of uniqueness of the inverse problem, there are several approaches that overcome this dilemma. Four of these approaches are discussed below:
The Empirical Approach
The empirical approach is based on the experience of the physician to recognize typical signal patterns associated with certain disorders. This means, that the diagnosis is based on the comparison of the recorded signal to a catalog of patterns associated with clinical disorders. If the signal is identified, the diagnosis can be made. This process has been formalized using a diagnostic tree. The diagnosis is reached through a sequence of logical steps that are derived statistically from the accumulated data base. This very same procedure may also be followed in creating a computer program to automate the diagnostic process (Macfarlane and Lawrie, 1974).
Imposition of Physiological Constraints
As noted, there is no unique solution to the inverse problem. By this we mean that more than one source configuration will generate fields that are consistent with the measurements (as demonstrated in Section 7.5.3). However, it may be possible to select from among these competing solutions one that at the same time meets physiological expectations. We say that this procedure involves the imposition of physiological constraints. Those that have been used successfully include a requirement that dipole sources point outward, that the activation sequence be continuous, that the signal and noise statistics lie in expected ranges, and so on (Pilkington and Plonsey, 1982).
Lead Field Theoretical Approach
It is possible to determine what is known as the sensitivity distribution of the lead. (To obtain it, we consider the relative voltage that would be measured at a lead as a function of the position and orientation of a unit dipole source; the lead sensitivity at a point is the relative lead voltage for a dipole whose direction is adjusted for maximum response.) One can then make decisions about the activity of the source based upon this information. This approach depends on the fact that each lead detects the component of the activation dipoles that are in the direction of the sensitivity of the lead.
 For all leads and for a statistically homogeneously distributed source the source of the detected signal is most probably located at that region of the source where the lead sensitivity is highest and oriented in the direction of the lead sensitivity. If the lead system is designed to detect certain equivalent source like dipole, quadrupole etc., the detected signal represents this equivalent source which is a simplified model of the real source. It must be pointed out that while this simplified model is not necessarily the source, it probably represents the main configuration of the source. This approach is discussed in detail later.
For all leads and for a statistically homogeneously distributed source the source of the detected signal is most probably located at that region of the source where the lead sensitivity is highest and oriented in the direction of the lead sensitivity. If the lead system is designed to detect certain equivalent source like dipole, quadrupole etc., the detected signal represents this equivalent source which is a simplified model of the real source. It must be pointed out that while this simplified model is not necessarily the source, it probably represents the main configuration of the source. This approach is discussed in detail later.
Simplified Source Model
The inverse problem may be solved by modeling the source of the bioelectric or biomagnetic signal and the volume conductor in the following way (Malmivuo, 1976; see Figure 7.9):
 At this point, the following question is of paramount importance: How good is the correspondence between the model and the actual physiology?
At this point, the following question is of paramount importance: How good is the correspondence between the model and the actual physiology?
 In the modeling method, certain practical considerations should be noted. First, to reduce the sensitivity to noise (both in the measured voltages and the measured geometry), the number of independent measurements at the body surface usually must greatly exceed the number of variables in the source model. The overspecified equations are then solved using least squares approximation (and possibly other constraints to achieve greater stability). Second, the sensitivity to noise increases greatly with an increase in the number of degrees of freedom. So, for example, although greater regional information could be obtained with greater number of multiple dipoles, the results could actually become useless if too large a number were selected. At present, the number of dipoles that can be satisfactorily described in an inverse process, in electrocardiography, is under 10..
In the modeling method, certain practical considerations should be noted. First, to reduce the sensitivity to noise (both in the measured voltages and the measured geometry), the number of independent measurements at the body surface usually must greatly exceed the number of variables in the source model. The overspecified equations are then solved using least squares approximation (and possibly other constraints to achieve greater stability). Second, the sensitivity to noise increases greatly with an increase in the number of degrees of freedom. So, for example, although greater regional information could be obtained with greater number of multiple dipoles, the results could actually become useless if too large a number were selected. At present, the number of dipoles that can be satisfactorily described in an inverse process, in electrocardiography, is under 10..
THE INVERSE PROBLEM WITH
THE MODELING METHOD
1
FOR THE SOURCE
The model should have a limited
number of independent variables
2
FOR THE VOLUME CONDUCTOR
The accuracy of the conductor model
must be as good as or better than
that of the source model
3
INDEPENDENT MEASUREMENTS
ARE MADE AS THE SOURCE MODEL
HAS INDEPENDENT VARIABLES
Now we have as many equations
as we have independent variables
and the source model may be evaluated
A NEW QUESTION, NAMELY:
4
Fig. 7.9. Solution of the inverse problem based on the modeling method.
7.5.5 Summary
In Section 7.5 we have described the problem of clinical interest in electrocardiography, magnetocardiography, electroencephalography, magnetoencephalography, etc. as the solution of an inverse problem. This solution involves determination of the source configuration responsible for the production of the electric signals that are measured. Knowledge of this distribution permits clinical diagnoses to be made in a straightforward deterministic way.
 As pointed out previously, from a theoretical standpoint the inverse problem has no unique solution. Added to this uncertainty is one based on the limitations arising from the limited data points and the inevitable contamination of noise. However, solutions are possible based on approximations of various kinds, including purely empirical recognition of signal patterns. Unfortunately, at this time, generalizations are not possible. As might be expected, this subject is currently under intense study.
As pointed out previously, from a theoretical standpoint the inverse problem has no unique solution. Added to this uncertainty is one based on the limitations arising from the limited data points and the inevitable contamination of noise. However, solutions are possible based on approximations of various kinds, including purely empirical recognition of signal patterns. Unfortunately, at this time, generalizations are not possible. As might be expected, this subject is currently under intense study.
REFERENCES



