9.1 INTRODUCTION
Many investigations in electrophysiology involve preparations that contain multiple cells. Examples include the nerve bundle, which consists of several thousand myelinated fibers; striated whole muscle, which may contain several thousand individual fibers; the heart, which has on the order of 1010 cells; and the brain, which also has about 1010 cells. In modeling the electric behavior of such preparations, the discrete cellular structure may be important (Spach, 1983). On the other hand, macroscopic (averaged) fields may adequately describe the phenomena of interest. In the latter case it is possible to replace the discrete structure with an averaged continuum that represents a considerable simplification. The goal of this chapter is to formulate a continuum representation of multicellular systems and then to explore its electric properties.9.2 CARDIAC MUSCLE CONSIDERED AS A CONTINUUM
The individual cells of cardiac muscle are roughly circular cylinders with a diameter of around 10 µm and length of 100 µm. The cells are stacked together a lot like bricks and are held together by tight junctions (these behave like "spot welds" of abutting cellular membranes). In addition, there are gap junctions, which provide for intercellular communication. The latter introduce a direct intercellular link which permits the movement of small molecules and ions from the intracellular space of one cell to that of its neighbors. The gap junction consists of hexagonal arrays of proteins called connexons, which completely penetrate the pre- and postjunctional abutting membranes. A central channel provides a resistive path for the movement of ions between the cells. Since such paths are limited in numbers and have very small cross-sectional areas, the effective junctional resistance is not negligible. In fact, the net junctional resistance between two adjoining cells is thought to be in the same order of magnitude as the end-to-end resistance of the myoplasm of either cell. On the other hand, this resistance is perhaps three orders of magnitude less than what it would be if current had to cross the two abutting membranes, highlighting the importance of the specialized gap-junctional pathway.
The gap junction consists of hexagonal arrays of proteins called connexons, which completely penetrate the pre- and postjunctional abutting membranes. A central channel provides a resistive path for the movement of ions between the cells. Since such paths are limited in numbers and have very small cross-sectional areas, the effective junctional resistance is not negligible. In fact, the net junctional resistance between two adjoining cells is thought to be in the same order of magnitude as the end-to-end resistance of the myoplasm of either cell. On the other hand, this resistance is perhaps three orders of magnitude less than what it would be if current had to cross the two abutting membranes, highlighting the importance of the specialized gap-junctional pathway.
 The length of the junctional channel is roughly that of the two plasma membranes (2
The length of the junctional channel is roughly that of the two plasma membranes (2  8.5 nm) through which it passes, plus the gap between membranes (3 nm) - or around 20 nm total. This length is very short in contrast with the length of a cell itself, since the ratio is roughly 20
8.5 nm) through which it passes, plus the gap between membranes (3 nm) - or around 20 nm total. This length is very short in contrast with the length of a cell itself, since the ratio is roughly 20  10-9/100
10-9/100  10-6 = 2
10-6 = 2  10-4. Consequently, since the total junctional and myoplasmic resistances are approximately equal but are distributed over lengths that are in the ratio of 2
10-4. Consequently, since the total junctional and myoplasmic resistances are approximately equal but are distributed over lengths that are in the ratio of 2  10-4, one can think of the junctional resistance as if it were concentrated at a point (i.e., it is a discrete resistance), whereas the myoplasmic resistance is spread out (or distributed) in character. These two types of resistance structures affect a propagating wave differently, as we demonstrate below.
10-4, one can think of the junctional resistance as if it were concentrated at a point (i.e., it is a discrete resistance), whereas the myoplasmic resistance is spread out (or distributed) in character. These two types of resistance structures affect a propagating wave differently, as we demonstrate below.
 A simplified representation of the intracellular space is given in Figure 9.1. The current and potential distributions within a cell are continuous. However, the junction, in view of its relatively short length but sizable resistance, must be considered as relatively discrete (lumped), and it introduces jumps in the voltage patterns, which accounts for the representation given in Figure 9.1.
A simplified representation of the intracellular space is given in Figure 9.1. The current and potential distributions within a cell are continuous. However, the junction, in view of its relatively short length but sizable resistance, must be considered as relatively discrete (lumped), and it introduces jumps in the voltage patterns, which accounts for the representation given in Figure 9.1.
 By confining our interest to potential and current field variations averaged over many cells, we can approximate the intracellular region described in Figure 9.1 by a continuous (averaged) volume conductor that fills the total space. The discrete and myoplasmic resistances are taken into account when the averaged values are obtained. The result is an intracellular conducting medium that is continuous..
By confining our interest to potential and current field variations averaged over many cells, we can approximate the intracellular region described in Figure 9.1 by a continuous (averaged) volume conductor that fills the total space. The discrete and myoplasmic resistances are taken into account when the averaged values are obtained. The result is an intracellular conducting medium that is continuous..
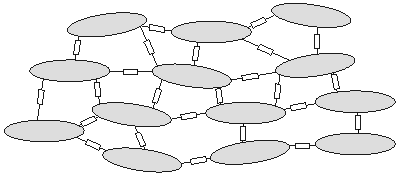
- Figure 9.1. Cells are represented as ellipsoidal-like regions within which the intracellular potential field is continuous. The intracellular spaces of adjoining cells are interconnected by junctional (discrete) resistances representing the effect of gap junctions. These introduce, on a cellular scale, discontinuities in the potential. If we confine our interest to variations on a macroscopic scale (compared to the size of a cell), then the medium can be considered to be continuous and fill all space. Such a medium is described by averaged properties, and the potentials that are evaluated must also be smoothed relative to a cellular dimension.
 One can apply the same considerations to the interstitial space. Although there are no discrete elements in this case, the space is nevertheless broken up by the presence of the cells. The fields associated with this continuum may be considered averaged over a distance of several cells - just as for the intracellular space.
One can apply the same considerations to the interstitial space. Although there are no discrete elements in this case, the space is nevertheless broken up by the presence of the cells. The fields associated with this continuum may be considered averaged over a distance of several cells - just as for the intracellular space.
 In summary, the complex cardiac tissue may be replaced by intracellular and interstitial continua, each filling the space occupied by the actual tissue. The parameters of the continua are derived by a suitable average of the actual structure. Both spaces are described by the same coordinate system. The membrane separates both domains at each point. This model has been described and has been designated as a bidomain (Miller and Geselowitz, 1978; Tung, 1978).
In summary, the complex cardiac tissue may be replaced by intracellular and interstitial continua, each filling the space occupied by the actual tissue. The parameters of the continua are derived by a suitable average of the actual structure. Both spaces are described by the same coordinate system. The membrane separates both domains at each point. This model has been described and has been designated as a bidomain (Miller and Geselowitz, 1978; Tung, 1978).
 In a more accurate model one can introduce the potential and current field variations on a cellular scale which are superimposed on variations that take place over longer spatial distances. Usually the former are of little interest when one is studying the macroscopic behavior of the tissue, and an averaged, smoothed (continuum) associated with the averaged fields is an acceptable and even a desirable simplification.
In a more accurate model one can introduce the potential and current field variations on a cellular scale which are superimposed on variations that take place over longer spatial distances. Usually the former are of little interest when one is studying the macroscopic behavior of the tissue, and an averaged, smoothed (continuum) associated with the averaged fields is an acceptable and even a desirable simplification.
9.3 MATHEMATICAL DESCRIPTION OF THE BIDOMAIN AND ANISOTROPY
The verbal description of the bidomain, discussed above, leads to definitive mathematical expressions for currents and potentials which, in view of the continuous structure, are in analytical form.
 We first introduce the concept of bidomain conductivity (σb). The intracellular and extracellular conductivities σi and σo, which we introduced earlier in this book, are microscopic conductivities. That is, they describe the conductivity at a point, and for an inhomogeneous medium they are functions of position. (Normally we consider σo a constant that tends to hide the fact that it is defined at each and every point.) The bidomain conductivities σib and σob are averaged values over several cells. That is why the bidomain conductivities depend on both the microscopic conductivity and the geometry.
We first introduce the concept of bidomain conductivity (σb). The intracellular and extracellular conductivities σi and σo, which we introduced earlier in this book, are microscopic conductivities. That is, they describe the conductivity at a point, and for an inhomogeneous medium they are functions of position. (Normally we consider σo a constant that tends to hide the fact that it is defined at each and every point.) The bidomain conductivities σib and σob are averaged values over several cells. That is why the bidomain conductivities depend on both the microscopic conductivity and the geometry.
 We now generalize Equation 7.2 (
We now generalize Equation 7.2 ( = - σ
= - σ Φ) to an anisotropic conducting medium where the current density components in the x, y, and z directions are proportional to the gradient of the intracellular scalar potential function Φi in the corresponding directions. Thus, for the intracellular domain, application of Ohm's law gives
Φ) to an anisotropic conducting medium where the current density components in the x, y, and z directions are proportional to the gradient of the intracellular scalar potential function Φi in the corresponding directions. Thus, for the intracellular domain, application of Ohm's law gives
 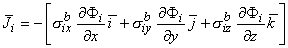 | (9.1) |
| where |  i i | = current density in the intracellular medium |
| Φi | = electric potential in the intracellular medium | |
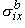 , , 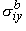 , , 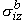 , , | = intracellular bidomain conductivities in the x, y, and z directions | |
 , ,  , ,  | = unit vectors in the x, y, and z directions |
 The proportionality constant (i.e., the bidomain conductivity) in each coordinate direction is considered to be different, reflecting the most general condition. Such anisotropicity is to be expected in view of the organized character of the tissue with preferential conducting directions. In fact, experimental observation has shown the conductivities to be highest along fiber directions relative to that in the cross-fiber direction.
The proportionality constant (i.e., the bidomain conductivity) in each coordinate direction is considered to be different, reflecting the most general condition. Such anisotropicity is to be expected in view of the organized character of the tissue with preferential conducting directions. In fact, experimental observation has shown the conductivities to be highest along fiber directions relative to that in the cross-fiber direction.
 Correspondingly, in the interstitial domain, assuming anisotropy here also, we have
Correspondingly, in the interstitial domain, assuming anisotropy here also, we have
 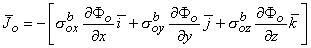 | (9.2) |
| where |  o o | = current density in the interstitial medium |
| Φo | = electric potential in the interstitial medium | |
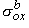 , , 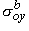 , , 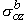 , , | = interstitial bidomain conductivities in the x, y, and z directions | |
 , ,  , ,  | = unit vectors in the x, y, and z directions |
 In general, the conductivity coefficients in the intracellular and interstitial domains can be expected to be different since they are, essentially, unrelated. Macroscopic measurements performed by Clerc (1976) and by Roberts and Scher (1982), which evaluated the coefficients in Equations 9.1 and 9.2 for cardiac muscle, are given in Table 9.1. These represent the only available measurements of these important parameters; unfortunately they differ substantially (partly because different methods were used), leaving a degree of uncertainty regarding the correct values.
In general, the conductivity coefficients in the intracellular and interstitial domains can be expected to be different since they are, essentially, unrelated. Macroscopic measurements performed by Clerc (1976) and by Roberts and Scher (1982), which evaluated the coefficients in Equations 9.1 and 9.2 for cardiac muscle, are given in Table 9.1. These represent the only available measurements of these important parameters; unfortunately they differ substantially (partly because different methods were used), leaving a degree of uncertainty regarding the correct values.
 The fiber orientation (axis) in these determinations was defined as the x coordinate; because of uniformity in the transverse plane, the conductivities in the y and z directions are equal.
The fiber orientation (axis) in these determinations was defined as the x coordinate; because of uniformity in the transverse plane, the conductivities in the y and z directions are equal.
measured by Clerc (1976) and Roberts and Scher (1982)
| |||||||||||||||
 The intracellular current density
The intracellular current density  i (Equation 9.1) and the interstitial current density
i (Equation 9.1) and the interstitial current density  o (Equation 9.2) are coupled by the need for current conservation. That is, current lost to one region must be gained by the other. The loss (or gain) is evaluated by the divergence; therefore,
o (Equation 9.2) are coupled by the need for current conservation. That is, current lost to one region must be gained by the other. The loss (or gain) is evaluated by the divergence; therefore,
 - -   i = i =    o = Im o = Im | (9.3) |
| where | Im | = transmembrane current per unit volume [µA/cm3]. |
Consider a large bundle of parallel striated muscle fibers lying in an insulating medium such as oil. If a large plate electrode is placed at each end and supplied a current step, and all fibers are assumed to be of essentially equal diameter, the response of each fiber will be the same. Consequently, to consider the behavior of the bundle, it is sufficient to model any single fiber, which then characterizes all fibers. Such a prototypical fiber and its associated interstitial space are described in Figure 9.2.
 In retrospect, the weakness in the bidomain model is that all fields are considered to be spatially averaged, with a consequent loss in resolution. On the other hand, the behavior of all fields is expressed by the differential Equations 9.1-9.3 which permits the use of mathematical approaches available in the literature on mathematical physics.
In retrospect, the weakness in the bidomain model is that all fields are considered to be spatially averaged, with a consequent loss in resolution. On the other hand, the behavior of all fields is expressed by the differential Equations 9.1-9.3 which permits the use of mathematical approaches available in the literature on mathematical physics.
9.4 ONE-DIMENSIONAL CABLE: A ONE-DIMENSIONAL BIDOMAIN
PRECONDITIONS:
Source: Bundle of parallel muscle fibers; a one-dimensional problem
Conductor: Finite, inhomogeneous, anisotropic bidomain
 The cross-sectional area of the interstitial space shown in Figure 9.2 is 1/N times the total interstitial cross-sectional area of the fiber bundle, where N is the number of fibers. Usually, the interstitial cross-sectional area is less than the intracellular cross-sectional area, since fibers typically occupy 70-80 % of the total area. Consequently, an electric representation of the preparation in Figure 9.2 is none other than the linear core-conductor model described in Figure 3.7 and Equations 3.41 and 3.42. In this case the model appropriately and correctly includes the interstitial axial resistance since current in that path is constrained to the axial direction (as it is for the intracellular space).
The cross-sectional area of the interstitial space shown in Figure 9.2 is 1/N times the total interstitial cross-sectional area of the fiber bundle, where N is the number of fibers. Usually, the interstitial cross-sectional area is less than the intracellular cross-sectional area, since fibers typically occupy 70-80 % of the total area. Consequently, an electric representation of the preparation in Figure 9.2 is none other than the linear core-conductor model described in Figure 3.7 and Equations 3.41 and 3.42. In this case the model appropriately and correctly includes the interstitial axial resistance since current in that path is constrained to the axial direction (as it is for the intracellular space).
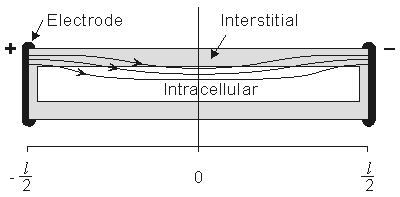
Figure 9.2. A prototypical fiber of a fiber bundle lying in oil and its response to the application of a steady current. Since the fiber is sealed, current flow into the intracellular space is spread out along the cylinder membrane. The ratio of interstitial to intracellular cross-sectional area of the single fiber reflects that of the bundle as a whole. The figure is not drawn to scale since usually the ratio of fiber length to fiber diameter is very large.
 A circuit representation for steady-state subthreshold conditions is given in Figure 9.3. In this figure, ri and ro are the intracellular and interstitial axial resistances per unit length, respectively. Since steady-state subthreshold conditions are assumed, the membrane behavior can be described by a constant (leakage) resistance of rm ohms times length (i.e., the capacitive membrane component can be ignored since
A circuit representation for steady-state subthreshold conditions is given in Figure 9.3. In this figure, ri and ro are the intracellular and interstitial axial resistances per unit length, respectively. Since steady-state subthreshold conditions are assumed, the membrane behavior can be described by a constant (leakage) resistance of rm ohms times length (i.e., the capacitive membrane component can be ignored since  V/
V/ t = 0 at steady state; hence the capacitive component of the membrane current imC = cm
t = 0 at steady state; hence the capacitive component of the membrane current imC = cm V/
V/ t = 0.
t = 0.
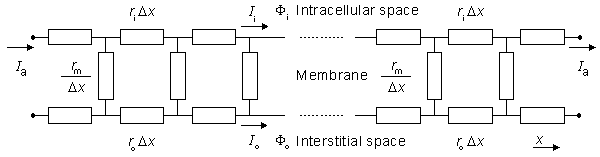
Figure 9.3. Linear core-conductor model circuit that corresponds to the preparation shown in Figure 9.2. The applied steady-state current Ia enters the interstitial space on the left and leaves on the right (at these sites Ii = 0). The steady-state subthreshold response is considered; hence the membrane is modeled as a resistance. Only the first few elements at each end are shown explicitly.
 The system, which is modeled by Figure 9.3, is in fact, a continuum. Accordingly it may be described by appropriate differential equations. In fact, these equations that follow, known as cable equations, have already been derived and commented on in Chapter 3. In particular, we found (Equation 3.46) that
The system, which is modeled by Figure 9.3, is in fact, a continuum. Accordingly it may be described by appropriate differential equations. In fact, these equations that follow, known as cable equations, have already been derived and commented on in Chapter 3. In particular, we found (Equation 3.46) that
 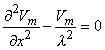 | (9.4) |
where the space constant, λ, is defined as
 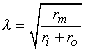 | (9.5) |
and has the dimension [cm]. This is the same as in Equation 3.48.
 In Equation 9.4, and in the following equations of this chapter, Vm describes the membrane potential relative to the resting potential. Consequently Vm corresponds to the V' of Chapter 3. Since, under resting conditions, there are no currents or signals (though there is a transmembrane voltage), interest is usually confined entirely to the deviations from the resting condition, and all reference to the resting potential ignored. The literature will be found to refer to the potential difference from rest without explicitly stating this to be the case, because it has become so generally recognized. For this more advanced chapter we have adopted this common practice and have refrained from including the prime symbol with Vm.
In Equation 9.4, and in the following equations of this chapter, Vm describes the membrane potential relative to the resting potential. Consequently Vm corresponds to the V' of Chapter 3. Since, under resting conditions, there are no currents or signals (though there is a transmembrane voltage), interest is usually confined entirely to the deviations from the resting condition, and all reference to the resting potential ignored. The literature will be found to refer to the potential difference from rest without explicitly stating this to be the case, because it has become so generally recognized. For this more advanced chapter we have adopted this common practice and have refrained from including the prime symbol with Vm.
 For the preparation in Figure 9.2, we anticipate a current of Ia to enter the interstitial space at the left-hand edge (x = - l /2), and as it proceeds to the right, a portion crosses the membrane to flow into the intracellular space. The process is reversed in the right half of the fiber, as a consequence of symmetry. The boundary condition of Ii = 0 at x = ± l /2 depends on the ends being sealed and the membrane area at the ends being a very small fraction of the total area. The argument is that although current may cross the end membranes, the relative area is so small that the relative current must likewise be very small (and negligible); this argument is supported by analytical studies (Weidmann, 1952). Since the transmembrane voltage is simply the transmembrane current per unit length times the membrane resistance times unit length (i.e., Vm = imrm), the antisymmetric (i.e., equal but opposite) condition expected for im must also be satisfied by Vm. Since the solution to the differential equation of 9.4 is the sum of hyperbolic sine and cosine functions, only the former has the correct behavior, and the solution to Equation 9.4 is necessarily:
For the preparation in Figure 9.2, we anticipate a current of Ia to enter the interstitial space at the left-hand edge (x = - l /2), and as it proceeds to the right, a portion crosses the membrane to flow into the intracellular space. The process is reversed in the right half of the fiber, as a consequence of symmetry. The boundary condition of Ii = 0 at x = ± l /2 depends on the ends being sealed and the membrane area at the ends being a very small fraction of the total area. The argument is that although current may cross the end membranes, the relative area is so small that the relative current must likewise be very small (and negligible); this argument is supported by analytical studies (Weidmann, 1952). Since the transmembrane voltage is simply the transmembrane current per unit length times the membrane resistance times unit length (i.e., Vm = imrm), the antisymmetric (i.e., equal but opposite) condition expected for im must also be satisfied by Vm. Since the solution to the differential equation of 9.4 is the sum of hyperbolic sine and cosine functions, only the former has the correct behavior, and the solution to Equation 9.4 is necessarily:
 Vm = Ka sinh(x/λ) Vm = Ka sinh(x/λ) | (9.6) |
| where | Ka | = a constant related to the strength of the supplied current, Ia. |
 We found earlier for the axial currents inside and outside the axon, in Equation 3.41 that
We found earlier for the axial currents inside and outside the axon, in Equation 3.41 that
 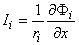 | (9.7a) |
 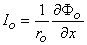 | (9.7b) |
If Equation 9.7 is applied at either end of the preparation (x = ± l /2), where  Φi /
Φi / x = 0 and where Io = Ia, we get
x = 0 and where Io = Ia, we get
 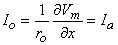 | (9.8) |
Substituting Equation 9.6 into Equation 9.8 permits evaluation of Ka as
 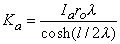 | (9.9) |
Consequently, substituting Equation 9.9 into Equation 9.6 results in
 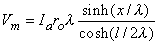 | (9.10) |
 We are interested in examining the intracellular and interstitial current behavior over the length of the fiber. The intracellular and interstitial currents are found by substituting Equation 9.10 into Equations 9.7a,b, while noting that Vm = Φi - Φo and that the intracellular and interstitial currents are constrained by the requirement that Ii + Io = Ia for all x due to conservation of current. The result is that
We are interested in examining the intracellular and interstitial current behavior over the length of the fiber. The intracellular and interstitial currents are found by substituting Equation 9.10 into Equations 9.7a,b, while noting that Vm = Φi - Φo and that the intracellular and interstitial currents are constrained by the requirement that Ii + Io = Ia for all x due to conservation of current. The result is that
 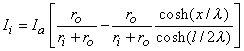 | (9.11) |
 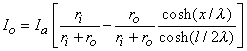 | (9.12) |
 The intracellular and interstitial currents described by Equations 9.11 and 9.12 are plotted in Figure 9.4 for the case that l = 20λ and where ri = ro/2. An important feature is that although the total current is applied to the interstitial space, a portion crosses the fiber membrane to flow in the intracellular space (a phenomenon described by current redistribution). We note that this redistribution of current from the interstitial to intracellular space takes place over an axial extent of several lambda. One can conclude that if the fiber length, expressed in lambdas, is say greater than 10, then in the central region, essentially complete redistribution has taken place. In this region, current-voltage relations appear as if the membrane were absent. Indeed, Vm
The intracellular and interstitial currents described by Equations 9.11 and 9.12 are plotted in Figure 9.4 for the case that l = 20λ and where ri = ro/2. An important feature is that although the total current is applied to the interstitial space, a portion crosses the fiber membrane to flow in the intracellular space (a phenomenon described by current redistribution). We note that this redistribution of current from the interstitial to intracellular space takes place over an axial extent of several lambda. One can conclude that if the fiber length, expressed in lambdas, is say greater than 10, then in the central region, essentially complete redistribution has taken place. In this region, current-voltage relations appear as if the membrane were absent. Indeed, Vm  0 and intracellular and interstitial currents are essentially axial and constant.
0 and intracellular and interstitial currents are essentially axial and constant.
 The total impedance presented to the electrodes by the fiber can be evaluated by dividing the applied voltage Va[Φo(-l /2) - Φo(l/2)] by the total current Ia. The value of Va can be found by integrating IoRo from x = -l /2 to x = l /2 using Equation 9.12. The result is that this impedance Z is
The total impedance presented to the electrodes by the fiber can be evaluated by dividing the applied voltage Va[Φo(-l /2) - Φo(l/2)] by the total current Ia. The value of Va can be found by integrating IoRo from x = -l /2 to x = l /2 using Equation 9.12. The result is that this impedance Z is
 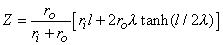 | (9.13) |
 If l
If l  λ and if ri and ro are assumed to be of the same order of magnitude, then the second term in the brackets of Equation 9.13 can be neglected relative to the first and the load is essentially that expected if the membrane were absent (a single domain resistance found from the parallel contribution of ro and ri). And if l
λ and if ri and ro are assumed to be of the same order of magnitude, then the second term in the brackets of Equation 9.13 can be neglected relative to the first and the load is essentially that expected if the membrane were absent (a single domain resistance found from the parallel contribution of ro and ri). And if l  λ , then tanh(l/2λ)
λ , then tanh(l/2λ)  l/2λ and Z = rol, reflecting the absence of any significant current redistribution; only the interstitial space supplies a current flow path. When neither inequality holds, Z reflects some intermediate degree of current redistribution.
l/2λ and Z = rol, reflecting the absence of any significant current redistribution; only the interstitial space supplies a current flow path. When neither inequality holds, Z reflects some intermediate degree of current redistribution.
 The example considered here is a simple illustration of the bidomain model and is included for two reasons. First, it is a one-dimensional problem and hence mathematically simple. Second, as we have noted, the preparation considered is, in fact, a continuum. Thus while cardiac muscle was approximated as a continuum and hence described by a bidomain, in this case a continuum is not just a simplifying assumption but, in fact, a valid description of the tissue.
The example considered here is a simple illustration of the bidomain model and is included for two reasons. First, it is a one-dimensional problem and hence mathematically simple. Second, as we have noted, the preparation considered is, in fact, a continuum. Thus while cardiac muscle was approximated as a continuum and hence described by a bidomain, in this case a continuum is not just a simplifying assumption but, in fact, a valid description of the tissue.
 Although we have introduced the additional simplification of subthreshold and steady-state conditions, the basic idea of current redistribution between intracellular and interstitial space should apply under less restrictive situations. It seems trivial to point out that whenever a multicellular region is studied, its separate intracellular and interstitial behavior needs to be considered in view of a possible discontinuity across the membrane (namely Vm). This is true whether the fibers are considered to be discrete or continuous..
Although we have introduced the additional simplification of subthreshold and steady-state conditions, the basic idea of current redistribution between intracellular and interstitial space should apply under less restrictive situations. It seems trivial to point out that whenever a multicellular region is studied, its separate intracellular and interstitial behavior needs to be considered in view of a possible discontinuity across the membrane (namely Vm). This is true whether the fibers are considered to be discrete or continuous..
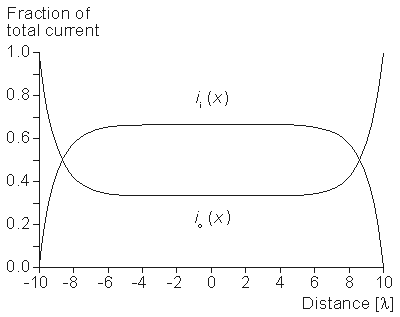
- Figure 9.4. Distribution of intracellular axial current ii(x) and interstitial axial current io(x) for the fiber described in Figure 9.2. The total length is 20λ and ri /ro = 1/2. Note that the steady-state conditions which apply for -7λ < x < 7λ , approximately suggest
 3 λ as an extent needed for current redistribution.
3 λ as an extent needed for current redistribution.9.5 SOLUTION FOR POINT-CURRENT SOURCE IN A THREE-DIMENSIONAL, ISOTROPIC BIDOMAIN
Precondtions:Source: Volume of muscle fibers; a three-dimensional problem
CONDUCTOR: Finite, inhomogeneous, anisotropic bidomain
As a further illustration of the bidomain model, we consider a volume of cardiac muscle and assume that it can be modeled as a bidomain, which is uniform and isotropic. Consequently, in place of Equations 9.1 and 9.2 we may write:
  i = -σib i = -σib  Φi Φi | (9.14) |
  o = -σob o = -σob  Φo Φo | (9.15) |
Here σib and σob have the dimensions of conductivity, and we refer to them as the isotropic intracellular and interstitial bidomain conductivities. Their values can be found as follows. Since each domain is considered to fill the total tissue space, which is larger than the actual occupied space, σib and σob are evaluated from the microscopic conductivities σi and σo by multiplying by the ratio of the actual to total volume, thus
 σib = σi vc σib = σi vc | (9.16) |
 σob = σo (1 - vc ) σob = σo (1 - vc ) | (9.16) |
where vc = the fraction of muscle occupied by the cells (= 0.70-0.85).
In these equations the conductivity on the left is a bidomain conductivity (and actually an averaged conductivity that could be measured only in an adequately large tissue sample), whereas the conductivity function on the right is the (microscopic) conductivity.
 Now the divergence of
Now the divergence of  o ordinarily evaluates the transmembrane current density, but we wish to include the possibility that an additional (applied) point current source has been introduced into the tissue. Assuming that an interstitial point source of strength Ia is placed at the coordinate origin requires
o ordinarily evaluates the transmembrane current density, but we wish to include the possibility that an additional (applied) point current source has been introduced into the tissue. Assuming that an interstitial point source of strength Ia is placed at the coordinate origin requires
    o = Imb + Iaδv o = Imb + Iaδv | (9.18) |
where δv is a three-dimensional Dirac delta function, which is defined as
 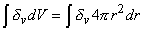 |
 = 1 if the volume includes the origin = 1 if the volume includes the origin |
 = 0 if the volume excludes the origin = 0 if the volume excludes the origin |
Equation 9.18 reduces to Equation 9.3 if Ia = 0.
 Substituting Equation 9.15 into Equation 9.18 gives
Substituting Equation 9.15 into Equation 9.18 gives
 - σob - σob  2Φo = Imb + Iaδv 2Φo = Imb + Iaδv | (9.19) |
where Imb = transmembrane current per unit volume [µA/cm3].
We also require the conservation of current (Equation 9.3):
    i = - Imb i = - Imb | (9.20) |
and substituting Equation 9.14 into Equation 9.20 gives
 σib σib  2Φi = Imb 2Φi = Imb | (9.21) |
Now multiplying Equation 9.19 by ρob (= 1/σob) and Equation 9.21 by ρib (= 1/σib) and summing results, we get
  2(Φi - Φo ) = 2(Φi - Φo ) =  2Vm = (ρib + ρob )Imb + ρoIaδv 2Vm = (ρib + ρob )Imb + ρoIaδv | (9.22) |
| where | ρib | = bidomain intracellular resistivity [kΩ·cm] |
| ρob | = bidomain interstitial resistivity [kΩ·cm] | |
| Imb | = transmembrane current per unit volume [µA/cm³] |
 Under subthreshold steady-state conditions, the capacitance can be ignored, and consequently, the membrane is purely resistive. If the surface-to-volume ratio of the cells is uniform and is designated , then the steady-state transmembrane current per unit volume (Imb ) is
Under subthreshold steady-state conditions, the capacitance can be ignored, and consequently, the membrane is purely resistive. If the surface-to-volume ratio of the cells is uniform and is designated , then the steady-state transmembrane current per unit volume (Imb ) is
 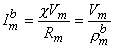 | (9.23) |
| where | bm | = transmembrane current per unit volume [µA/cm³] |
| im | = surface to volume ratio of the cell [1/cm] | |
| Vm | = membrane voltage [mV] | |
| Rm | = membrane resistance times unit area [kΩ·cm²] |
and where
 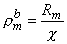 | (9.24) |
is membrane resistance times unit volume [kΩ cm]. (The variable ρmb has the dimension of resistivity, because it represents the contribution of the membranes to the leakage resistivity of a medium including intracellular and extracellular spaces and the membranes.)
cm]. (The variable ρmb has the dimension of resistivity, because it represents the contribution of the membranes to the leakage resistivity of a medium including intracellular and extracellular spaces and the membranes.)
 Substituting Equation 9.23 into Equation 9.22 results in the desired differential equation for Vm, namely
Substituting Equation 9.23 into Equation 9.22 results in the desired differential equation for Vm, namely
 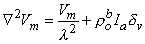 | (9.25) |
where
 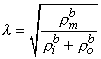 | (9.26) |
The three-dimensional isotropic space constant, defined by Equation 9.26, is in the same form and has the same dimension [cm] as we evaluated for one-dimensional preparations described by Equation 9.5.
 In view of the spherical symmetry, the Laplacian of Vm (in Equation 9.25) which in spherical coordinates has the form
In view of the spherical symmetry, the Laplacian of Vm (in Equation 9.25) which in spherical coordinates has the form
 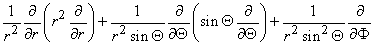 |
contains only an r dependence, so that we obtain
 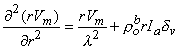 | (9.27) |
The solution when r 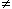 0 is
0 is
 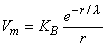 | (9.28) |
One can take into account the delta function source δv by imposing a consistent boundary condition at the origin. With this point of view, KB, in Equation 9.28, is chosen so that the behavior of Vm for r  0 is correct. This condition is introduced by integrating each term in Equation 9.25 through a spherical volume of radius r
0 is correct. This condition is introduced by integrating each term in Equation 9.25 through a spherical volume of radius r  0 centered at the origin. The volume integral of the term on the left-hand side of Equation 9.25 is performed by converting it to a surface integral using the divergence theorem of vector analysis. One finds that
0 centered at the origin. The volume integral of the term on the left-hand side of Equation 9.25 is performed by converting it to a surface integral using the divergence theorem of vector analysis. One finds that
 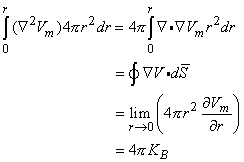 | (9.29) |
(The last step is achieved by substituting from Equation 9.28 for Vm.)
 Substituting Equation 9.28 for Vm in the second term of Equation 9.25 gives
Substituting Equation 9.28 for Vm in the second term of Equation 9.25 gives
 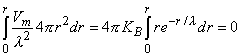 | (9.30) |
whereas the third term
 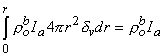 | (9.31) |
Equation 9.31 follows from the definition of the Dirac delta function δv given for Equation 9.18. Substituting Equations 9.29-9.31 into Equation 9.25 demonstrates that Vm will have the correct behavior in the r neighborhood of the origin if KB satisfies
 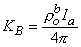 | (9.32) |
Substituting Equation 9.32 into Equation 9.28 finally results in
 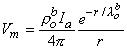 | (9.33) |
 If the scalar function Ψ is defined as
If the scalar function Ψ is defined as
 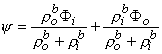 | (9.34) |
then, from Equations 9.19 and 9.21, we have
 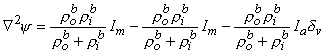 | (9.35) |
Consequently,
 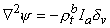 | (9.36) |
where
 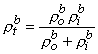 |
and ρtb is the total tissue impedance in the absence of a membrane (referred to as a bulk impedance). We note, in Equation 9.36, that Ψ satisfies a (monodomain) Poisson equation. In fact, Ψ is the field of a point source at the origin and is given by
 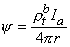 | (9.37) |
Since Vm = Φi - Φo, one can express either Φi or Φo in terms of Vm and Ψ by using Equation 9.34. The result is
 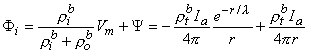 | (9.38) |
 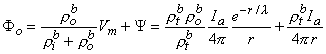 | (9.39) |
where Equations 9.33 and 9.37 were substituted into Equation 9.38 and 9.39 to obtain the expressions following the second equal signs. This pair of equations describes the behavior of the component fields. Note that the boundary condition
 Φi/
Φi/ r = 0 at r
r = 0 at r  0 is satisfied by Equation 9.38. This condition was implied in formulating Equation 9.19, where the total source current is described as interstitial.
0 is satisfied by Equation 9.38. This condition was implied in formulating Equation 9.19, where the total source current is described as interstitial.
9.6 FOUR-ELECTRODE IMPEDANCE METHOD APPLIED TO AN ISOTROPIC BIDOMAIN
For a homogeneous isotropic tissue, the experimental evaluation of its resistivity is often performed using the four-electrode method (Figure 9.5). In this method, four equally spaced electrodes are inserted deep into the tissue. We assume that the overall extent of the electrode system is small compared to its distance to a boundary, so that the volume conductor can be approximated as unlimited in extent (unbounded). The outer electrodes carry an applied current (i.e., Ia and -Ia) whereas the inner electrodes measure the resulting voltage. The resistivity ρ (Heiland, 1940)
is given by
 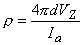 | (9.40) |
| where | VZ | = measured voltage and |
| d | = interelectrode spacing |
 The advantage in the use of the four-electrode method arises from the separation of the current-driving and voltage-measuring circuits. In this arrangement the unknown impedance at the electrode-tissue interface is important only in the voltage- measuring circuit, where it adds a negligible error that depends on the ratio of electrode impedance to input impedance of the amplifier (ordinarily many times greater).
The advantage in the use of the four-electrode method arises from the separation of the current-driving and voltage-measuring circuits. In this arrangement the unknown impedance at the electrode-tissue interface is important only in the voltage- measuring circuit, where it adds a negligible error that depends on the ratio of electrode impedance to input impedance of the amplifier (ordinarily many times greater).
 For an isotropic bidomain the four-electrode method also may be used to determine the intracellular and interstitial conductivities ρib and bo. In this case, at least two independent observations must be made since there are two unknowns. If we assume that a current source of strength Ia is placed on the z axis at a distance of 3d/2 (i.e., at (0, 0, 1.5d)) and source of strength -Ia at (0, 0, -1.5d) (as described in Fig. 9.5, where d is the spacing between adjacent electrodes), then the resulting interstitial electric fields can be calculated from Equation 9.39 using superposition. In particular, we are interested in the voltage (VZ) that would be measured by the voltage electrodes, where
For an isotropic bidomain the four-electrode method also may be used to determine the intracellular and interstitial conductivities ρib and bo. In this case, at least two independent observations must be made since there are two unknowns. If we assume that a current source of strength Ia is placed on the z axis at a distance of 3d/2 (i.e., at (0, 0, 1.5d)) and source of strength -Ia at (0, 0, -1.5d) (as described in Fig. 9.5, where d is the spacing between adjacent electrodes), then the resulting interstitial electric fields can be calculated from Equation 9.39 using superposition. In particular, we are interested in the voltage (VZ) that would be measured by the voltage electrodes, where
 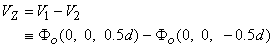 | (9.41) |
Application of Equation 9.39 to the point source Ia (imagine for this calculation that the origin of coordinates is at this point) shows that it contributes to VZ an amount VZs, namely
 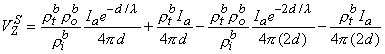 | (9.42) |
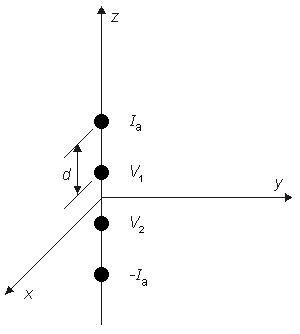
- Figure 9.5. Four-electrode method for the determination of tissue impedance. The electrode is embedded in the tissue. The outer elements carry the applied current ± Ia while the inner elements measure the resulting voltage (VZ = V1 - V2 ). The electrodes are spaced a distance (a) from each other (equispaced). For a uniform isotropic monodomain, the resistivity ρ = 2πdVZ /Ia.
This result is, of course, independent of the actual coordinate origin since it is a unique physical entity. Correspondingly, the point sink (i.e., the negative source of -Ia) contributes an amount VZk given by
 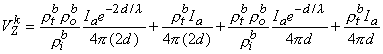 | (9.43) |
Summing Equations 9.42 and 9.43 yields the voltage that would be measured at the voltage electrodes, namely
 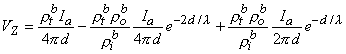 | (9.44) |
or
 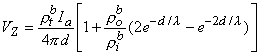 | (9.45) |
If measurement of VZ and Ia is made with d  λ then, according to Equation 9.45, this condition results in a relationship
λ then, according to Equation 9.45, this condition results in a relationship
 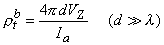 | (9.46) |
and the bulk resistivity (ρtb = ρob ρib /(ρob + ρib )) is obtained. If a second measurement is made with d 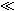 λ , then according to Equation 9.45 we have
λ , then according to Equation 9.45 we have
 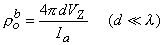 | (9.47) |
and only the interstitial resistivity is evaluated (as expected since over the relatively short distance no current is redistributed to the intracellular space, and hence only the interstitial resistivity influences the voltage-current behavior). The two experiments permit determination of both ρob and ρib .
Clerc L (1976): Directional differences of impulse spread in trabecular muscle from mammalian heart. J. Physiol. (Lond.) 225:(2) 335-46.
Heiland CA (1940): Geophysical Exploration, 1013 pp. Prentice-Hall, Englewood Cliffs, N.J.
Miller WT, Geselowitz DB (1978): Simulation studies of the electrocardiogram, I. The normal heart. Circ. Res. 43:(2) 301-15.
Plonsey R, Barr RC (1986): A critique of impedance measurements in cardiac tissue. Ann. Biomed. Eng. 14: 307-22.
Roberts DE, Scher AM (1982): Effects of tissue anisotropy on extracellular potential fields in canine myocardium in situ. Circ. Res. 50: 342-51.
Spach MS (1983): The discontinuous nature of electrical propagation in cardiac muscle. Ann. Biomed. Eng. 11: 209-61.
Tung L (1978): A bidomain model for describing ischemic myocardial D-C potentials. M.I.T. Cambridge, Mass., (Ph.D. thesis)
Weidmann S (1952): The electrical constants of Purkinje fibers. J. Physiol. (Lond.) 118: 348-60.
 One important conclusion to be drawn from the work presented in this chapter is illustrated by the contrast of Equations 9.45 and 9.40. The interpretation of a four-electrode measurement depends on whether the tissue is a monodomain or bidomain. If it is a bidomain, then the monodomain interpretation can lead to considerable error, particularly if d
One important conclusion to be drawn from the work presented in this chapter is illustrated by the contrast of Equations 9.45 and 9.40. The interpretation of a four-electrode measurement depends on whether the tissue is a monodomain or bidomain. If it is a bidomain, then the monodomain interpretation can lead to considerable error, particularly if d 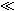 λ or if d
λ or if d  λ . For such situations Equation 9.45 must be used. When the tissue is an anisotropic bidomain, it is even more important to use a valid (i.e., Equation 9.45) model in the analysis of four-electrode measurements (Plonsey and Barr, 1986)..
λ . For such situations Equation 9.45 must be used. When the tissue is an anisotropic bidomain, it is even more important to use a valid (i.e., Equation 9.45) model in the analysis of four-electrode measurements (Plonsey and Barr, 1986)..
REFERENCES



