24.1 INTRODUCTION
In this chapter we explore the use of cardiac stimulation to terminate arrhythmias. Our focus is mainly on defibrillation, in which very high energy shocks are applied for the purpose of ending the fibrillation (which is otherwise lethal). The application of biophysical principles and the use of simulation and modeling that characterizes other chapters in this book is greatly limited here. The reason is that the mechanism of both fibrillation and defibrillation are incompletely understood. The subject of ventricular fibrillation is the center of much attention from clinical and basic scientists since it is one of the leading causes of death in the Western world (1,200 daily). It has been established that the underlying cause is atherosclerotic coronary artery disease, which results in occlusion of coronary perfusion. In many cases the more recent technique of the implantable defibrillator offers a more successful approach to the control of life-threatening arrhythmia than antiarrhythmic drugs. The subject is therefore of great importance and represents a potential area for application of the electrophysiological principles developed in this book.
The subject of ventricular fibrillation is the center of much attention from clinical and basic scientists since it is one of the leading causes of death in the Western world (1,200 daily). It has been established that the underlying cause is atherosclerotic coronary artery disease, which results in occlusion of coronary perfusion. In many cases the more recent technique of the implantable defibrillator offers a more successful approach to the control of life-threatening arrhythmia than antiarrhythmic drugs. The subject is therefore of great importance and represents a potential area for application of the electrophysiological principles developed in this book.
24.2 MECHANISMS OF FIBRILLATION
As noted in the introduction, the underlying cause of most cardiac arrhythmias is coronary artery disease involving the development of atherosclerotic plaques. These narrow and occlude the arterial vessels, resulting in ischemia and infarction of cardiac tissue. The electrophysiological properties of ischemic and infarcted tissue in turn provide opportunities for reentrant arrhythmias.24.2.1 Reentry
Reentry in a ring of cardiac tissue was studied by Mines (1913) whose observations are still appropriate today. In Figure 24.1A, a stimulus at the single site within the ring gives rise to propagation in opposite directions around the ring. These activation waves meet on the opposite side of the diameter from the stimulation site, and collision results. Since at the collision site all neighboring tissue is absolutely refractory, the excitable tissue volume is reduced to zero, and excitation/propagation is terminated. There is no reentry, and this reflects normal cardiac behavior. In Figure 24.1B the cross-hatched region is assumed to block propagation which is initiated in the clockwise direction. (The block arises possibly because the cells in this region are still in their refractory period.) Consequently, propagation takes place only counterclockwise, following an "alternate path." When propagation finally reaches the region of block, if it is no longer refractory then activation will continue past this site to the starting point and then continue around a second time. This pattern can now continue for successive periods; it is a description of reentry. The behavior of the hatched region is described as unidirectional block since, as it turned out, propagation was successful in the counterclockwise direction but not in the clockwise direction.
In Figure 24.1B the cross-hatched region is assumed to block propagation which is initiated in the clockwise direction. (The block arises possibly because the cells in this region are still in their refractory period.) Consequently, propagation takes place only counterclockwise, following an "alternate path." When propagation finally reaches the region of block, if it is no longer refractory then activation will continue past this site to the starting point and then continue around a second time. This pattern can now continue for successive periods; it is a description of reentry. The behavior of the hatched region is described as unidirectional block since, as it turned out, propagation was successful in the counterclockwise direction but not in the clockwise direction.
 Observation of Figure 24.1 suggests the following conditions for reentry: (1) An area of unidirectional block must be present. (2) Activation, while blocked around one path, must be able to propagate around an alternate path (the counterclockwise direction in Figure 24.1). (3) The propagation time around the alternate path must be greater than the total refractory period of the cells in the unidirectional block. One defines the wavelength as the distance traveled during the duration of the refractory period. (It can be calculated as the product of conduction velocity times refractory period duration.) In Figure 24.1B the wavelength must be shorter than the counterclockwise path length in order for reentry to take place. This requirement can be facilitated by a shortened refractory period of the tissue, slow conduction velocity, or both..
Observation of Figure 24.1 suggests the following conditions for reentry: (1) An area of unidirectional block must be present. (2) Activation, while blocked around one path, must be able to propagate around an alternate path (the counterclockwise direction in Figure 24.1). (3) The propagation time around the alternate path must be greater than the total refractory period of the cells in the unidirectional block. One defines the wavelength as the distance traveled during the duration of the refractory period. (It can be calculated as the product of conduction velocity times refractory period duration.) In Figure 24.1B the wavelength must be shorter than the counterclockwise path length in order for reentry to take place. This requirement can be facilitated by a shortened refractory period of the tissue, slow conduction velocity, or both..
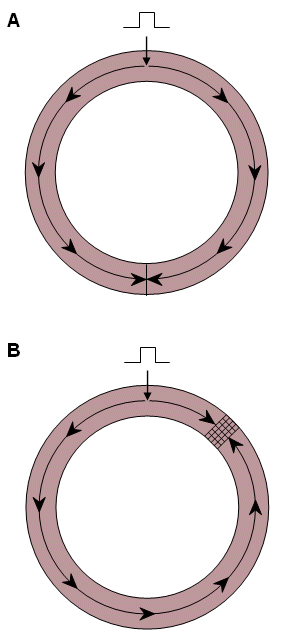
- Fig. 24.1 Demonstration of conditions that lead to reentry.
 (A) In the normal tissue collision and annihilation prevent reentry from occurring.
(A) In the normal tissue collision and annihilation prevent reentry from occurring.
 (B) The cross-hatched area is functionally a unidirectional block and facilitates a counterclockwise circus movement.
(B) The cross-hatched area is functionally a unidirectional block and facilitates a counterclockwise circus movement.In normal activation of the heart propagation ceases when conduction reaches the boundaries of the myocardium. At this point, there is no longer any tissue available that is not in the refractory state. When the next beat is initiated at the SA node, the entire heart is quiescent, and the ensuing process is a repetition of previous ones. The significance of the occurrence of reentry is that the normal pacemaker-initiated process is bypassed. If, as is usual, the activation cycle is very short, then the tissues undergoing reentry serve is a stimulus site for driving the entire heart at a faster rate (tachycardia).
 In the example given above, the basis for the unidirectional block was described as due to inhomogeneity of the refractory period. Although this is the most likely cause, there are other mechanisms as well. One arises from the anisotropy of cardiac tissue. The reason is that the axial resistance is much less along than transverse to the fiber direction, and this gives rise to anisotropy in velocity. In addition, there are differences in the organization of intercellular junctions which appears to increase the safety factor for transverse propagation compared to longitudinal (Spach and Dolber, 1985). Consequently, in the case of a premature excitation, propagation along the fiber direction can be blocked yet take place in the transverse direction, resulting in a reentry loop as in Figure 24.1B.
In the example given above, the basis for the unidirectional block was described as due to inhomogeneity of the refractory period. Although this is the most likely cause, there are other mechanisms as well. One arises from the anisotropy of cardiac tissue. The reason is that the axial resistance is much less along than transverse to the fiber direction, and this gives rise to anisotropy in velocity. In addition, there are differences in the organization of intercellular junctions which appears to increase the safety factor for transverse propagation compared to longitudinal (Spach and Dolber, 1985). Consequently, in the case of a premature excitation, propagation along the fiber direction can be blocked yet take place in the transverse direction, resulting in a reentry loop as in Figure 24.1B.
24.2.2 Reentry with and Without Anatomic Obstacles
In Figure 24.1 we assumed the circular path to be defined by a nonconducting interior obstacle. In the absence of this obstacle, one would wonder whether the circular path would maintain itself in view of a possible "short-circuiting" by conduction along a diagonal. However, reentry can be demonstrated even in the absence of an obstacle, as can be seen in Figure 24.2 (from the experimental work of Allessie, Bonke, and Scopman, 1976). Figure 24.2.A describes the activation pattern resulting from regularly paced (500 ms interval) stimuli in an isolated rabbit left atrial preparation. A premature stimulus is applied at the central position (the large dot shown in the figure) after a 56 ms delay. Figure 24.2D describes the length of the refractory period at different points, and this helps explain the response to the premature stimulus shown in Figure 24.2B. One notes propagation to the left into recovered tissue and block to the right (double bars) where the refractory period has not ended. But propagation winds back to this region after a delay so that the region of block is now excitable. Figure 24.2C shows the first cycle of tachycardia; a reentrant circuit (called a circus movement), it does not involve a nonconducting obstacle but, rather, is based on the inhomogeneous recovery properties of the preparation.
Figure 24.2.A describes the activation pattern resulting from regularly paced (500 ms interval) stimuli in an isolated rabbit left atrial preparation. A premature stimulus is applied at the central position (the large dot shown in the figure) after a 56 ms delay. Figure 24.2D describes the length of the refractory period at different points, and this helps explain the response to the premature stimulus shown in Figure 24.2B. One notes propagation to the left into recovered tissue and block to the right (double bars) where the refractory period has not ended. But propagation winds back to this region after a delay so that the region of block is now excitable. Figure 24.2C shows the first cycle of tachycardia; a reentrant circuit (called a circus movement), it does not involve a nonconducting obstacle but, rather, is based on the inhomogeneous recovery properties of the preparation.
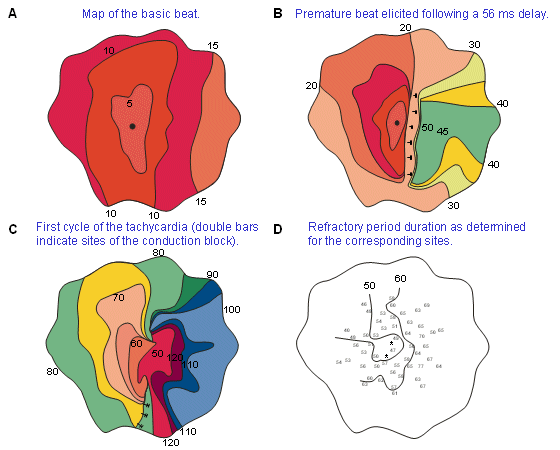
Fig. 24.2 Actual maps of the spread of activation during the onset of tachycardia induced by a premature stimulus in an isolated rabbit heart atrial preparation.
 (A) Map of the basic beat.
(A) Map of the basic beat.
 (B) Premature beat elicited following a 56 ms delay.
(B) Premature beat elicited following a 56 ms delay.
 (C) First cycle of the tachycardia (double bars indicate sites of the conduction block).
(C) First cycle of the tachycardia (double bars indicate sites of the conduction block).
 (D) Refractory period duration as determined for the corresponding sites. (From Allessie, Bonke, and Schopman, 1976.)
(D) Refractory period duration as determined for the corresponding sites. (From Allessie, Bonke, and Schopman, 1976.)
 The smallest path that permits this circular-type propagation (i.e., the wavelength of the circuit) has been called the leading circle (Allessie, Bonke, and Schopman, 1977). As before the wavelength can be evaluated as the product of velocity and refractory period. However, in this type of reentry the refractory period and the conduction velocity are interrelated. The pathway length of a reentrant circuit of the leading circle type is approximately 8 mm.
The smallest path that permits this circular-type propagation (i.e., the wavelength of the circuit) has been called the leading circle (Allessie, Bonke, and Schopman, 1977). As before the wavelength can be evaluated as the product of velocity and refractory period. However, in this type of reentry the refractory period and the conduction velocity are interrelated. The pathway length of a reentrant circuit of the leading circle type is approximately 8 mm.
 The reentrant circuit is seen as a consequence of the inhomogeneity in refractoriness in Figure 24.2D. Such conditions (along with short refractory periods, and slow conduction) are found in ischemic myocardium. An examination of successive beats shows the position around which propagation takes place to shift continuously. The reason is that the cells in the region of the vortex during one cycle may show a large action potential (hence be part of the circulating wave) in the following cycle. In spite of this beat-to-beat variation the reentry in the case of tachycardia is relatively orderly and results in a regular rhythm. Random reentry, which characterizes fibrillation, is characterized by pathways whose size and location are continually changing. In addition, several independent wavefronts may be present simultaneously and interact with one another. The resulting rhythm is consequently relatively irregular and chaotic.
The reentrant circuit is seen as a consequence of the inhomogeneity in refractoriness in Figure 24.2D. Such conditions (along with short refractory periods, and slow conduction) are found in ischemic myocardium. An examination of successive beats shows the position around which propagation takes place to shift continuously. The reason is that the cells in the region of the vortex during one cycle may show a large action potential (hence be part of the circulating wave) in the following cycle. In spite of this beat-to-beat variation the reentry in the case of tachycardia is relatively orderly and results in a regular rhythm. Random reentry, which characterizes fibrillation, is characterized by pathways whose size and location are continually changing. In addition, several independent wavefronts may be present simultaneously and interact with one another. The resulting rhythm is consequently relatively irregular and chaotic.
 Figure 24.3 shows the activation patterns of three successive "beats" during ventricular fibrillation. These illustrate the multiple regions of conduction block which shift continuously. One can also determinate collision and fusion of wavefronts, and interrupted circus movements. The diameters of such circuits vary between 8 and 30 mm. Because of the complexity of the patterns, maps such as these, which describe behavior only on the bounding surface, leave many of the details hidden from view (in the third dimension).
Figure 24.3 shows the activation patterns of three successive "beats" during ventricular fibrillation. These illustrate the multiple regions of conduction block which shift continuously. One can also determinate collision and fusion of wavefronts, and interrupted circus movements. The diameters of such circuits vary between 8 and 30 mm. Because of the complexity of the patterns, maps such as these, which describe behavior only on the bounding surface, leave many of the details hidden from view (in the third dimension).
 With very slow conduction (in, say, elevated K+ at perhaps 5 cm/s), and very short refractory periods (50 - 100 ms), one can have a very short wavelengths (<1 cm). These give rise to reentrant circuits characterized as microreentrant. It has been thought that such circuits might be seen in intact hearts with acute regional ischemia.
With very slow conduction (in, say, elevated K+ at perhaps 5 cm/s), and very short refractory periods (50 - 100 ms), one can have a very short wavelengths (<1 cm). These give rise to reentrant circuits characterized as microreentrant. It has been thought that such circuits might be seen in intact hearts with acute regional ischemia.
 In addition to the reentry described above which arises in ischemic and infarcted myocardium, reentry can also occur that utilizes structures of the heart. Clinical examples may be found that demonstrate reentry involving the AV junction, the His-Purkinje system, the SA node, and so on. We omit further details since our goal here is only to develop sufficient background for the subject of defibrillation.
In addition to the reentry described above which arises in ischemic and infarcted myocardium, reentry can also occur that utilizes structures of the heart. Clinical examples may be found that demonstrate reentry involving the AV junction, the His-Purkinje system, the SA node, and so on. We omit further details since our goal here is only to develop sufficient background for the subject of defibrillation.
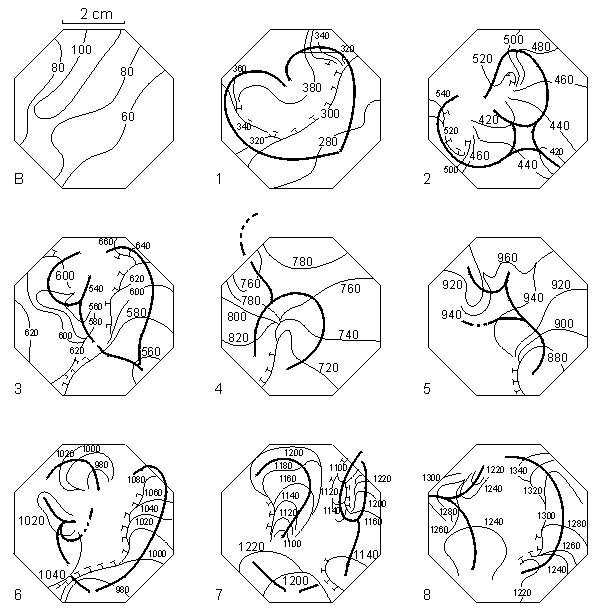
Fig. 24.3 Activation patterns of eight successive activations during ischemia-induced ventricular fibrillation in an isolated perfused pig heart following premature stimulus. Reentry occurs between first and second activation. These patterns demonstrate the presence of multiple wavefronts, and both collision and fusion of wavefronts. Beat 7 shows microcircus movement. (From Janse et al., 1980.)
24.3 THEORIES OF DEFIBRILLATION
24.3.1 Introduction
The basic goal in defibrillation is to interfere, electrically, with the reentry circuits to bring this electric activity to a halt. Since the reentrant circuits lie throughout the heart, achieving this goal requires an adequate stimulating field at all points within the heart. This is in contrast to pacemaking, where an adequate stimulus was required only at one site. For pacemaking, an empirical applied current density adequate for stimulation is 5.0 mA/cm² which, assuming a tissue resistivity of 500 Ωcm, gives an applied field of 2.5 V/cm. This compares with other estimates of 1 V/cm. But for defibrillation, empirical studies show a need for around 8 V/cm throughout the heart. One can speculate that with an applied electric field that is 3 - 6 times normal threshold much of the relatively refractory tissue as well as recovered tissue that is facing the advancing wavefronts can be activated. This volume is synchronously activated and consequently should greatly modify the activation pattern that would otherwise arise. This, however, is about as close to a defibrillatory mechanism as understood at this time. In spite of this situation, a great deal is known about defibrillation through many animal experiments that have been performed. In the following, we summarize the main ideas.
One can speculate that with an applied electric field that is 3 - 6 times normal threshold much of the relatively refractory tissue as well as recovered tissue that is facing the advancing wavefronts can be activated. This volume is synchronously activated and consequently should greatly modify the activation pattern that would otherwise arise. This, however, is about as close to a defibrillatory mechanism as understood at this time. In spite of this situation, a great deal is known about defibrillation through many animal experiments that have been performed. In the following, we summarize the main ideas.
24.3.2 Critical Mass Hypothesis
In the critical mass hypothesis the basic mechanism of defibrillation is assumed to be the interruption of activation fronts by depolarization of refractory and recovered tissue by the defibrillating field. However, it is further assumed that not all such tissue is necessarily activated to terminate fibrillation; instead, only a critical amount (often suggested to be 75% or more) is required. A comprehensive study of this hypothesis was undertaken by Witkowski and colleagues (Witkowski, Penkoske, and Plonsey, 1990). These authors note that although the interval between activations (ACT-ACT) during fibrillation is irregular, it nevertheless satisfies a definite statistical description. This was used to test whether, following a shock, the electric activity was continuing or fibrillation had been successfully annihilated. This was examined at each of their 120 surface electrode locations. The shock magnitude (as described by its electric field strength) was also evaluated at each electrode. The authors concluded that with unsuccessful defibrillation at least one ventricular site could be clearly identified where defibrillation had failed. But in the case of successful defibrillation either all sites showed an absence of fibrillating activity in the post- shock period or a single site had a self-terminating fibrillation (in one to three activations). The latter single site was located in a region of minimum defibrillatory field strength. From this they concluded that a critical mass less than 100% could lead to successful defibrillation. An alternative hypothesis, called the upper limit of vulnerability hypothesis has been advanced by Chen and colleagues (Chen, Wolf, and Ideker, 1991). In the referenced paper they disputed the conclusions drawn by Witkowski et al. and suggested that the same data (including their own experiments) required a different interpretation. They agreed with Witkowski et al. that following unsuccessful defibrillation the site of earliest activation is at the lowest defibrillatory field strength. However, their statistical analysis showed that the electrophysiological behavior at this site is definitely affected by the shock. They concluded that the shock did, in fact, defibrillate. However, in the absence of a shock intensity great enough, fibrillation was reinitiated.
An alternative hypothesis, called the upper limit of vulnerability hypothesis has been advanced by Chen and colleagues (Chen, Wolf, and Ideker, 1991). In the referenced paper they disputed the conclusions drawn by Witkowski et al. and suggested that the same data (including their own experiments) required a different interpretation. They agreed with Witkowski et al. that following unsuccessful defibrillation the site of earliest activation is at the lowest defibrillatory field strength. However, their statistical analysis showed that the electrophysiological behavior at this site is definitely affected by the shock. They concluded that the shock did, in fact, defibrillate. However, in the absence of a shock intensity great enough, fibrillation was reinitiated.
 There is agreement on several important points. First, typical shocks generate field strengths throughout the heart that are quite variable. Placing defibrillating electrodes on the right atrium and left ventricular apex of a dog, Ideker et al. (1987) found the potential field gradient to vary over a 15:1 range on the epicardium. Second the site of earliest measured activity following unsuccessful defibrillation coincided with the region with the lowest shock field strength. These conclusions support the idea that the goal of a defibrillating electrode system is the generation of a uniform field within the heart. (This avoids having damagingly high fields in some spots to ensure an adequate field elsewhere.) The minimum field for successful defibrillation was found by both groups to lie in the range of 3-9 V/cm.
There is agreement on several important points. First, typical shocks generate field strengths throughout the heart that are quite variable. Placing defibrillating electrodes on the right atrium and left ventricular apex of a dog, Ideker et al. (1987) found the potential field gradient to vary over a 15:1 range on the epicardium. Second the site of earliest measured activity following unsuccessful defibrillation coincided with the region with the lowest shock field strength. These conclusions support the idea that the goal of a defibrillating electrode system is the generation of a uniform field within the heart. (This avoids having damagingly high fields in some spots to ensure an adequate field elsewhere.) The minimum field for successful defibrillation was found by both groups to lie in the range of 3-9 V/cm.
 While the aforementioned studies are valuable to the development of an understanding of fibrillation, they do not actually elucidate a mechanism in the electrophysiological sense. The only way a shock can influence the behavior of fibrillating cells is through the induced transmembrane potential. The result could be activation of a cell in the resting or relative refractory period. However one has to keep in mind that fibrillating cells do not behave in the same way as normal cells. Furthermore, the question is not simply what happens to individual cells but how the interaction of these cells is modified.
While the aforementioned studies are valuable to the development of an understanding of fibrillation, they do not actually elucidate a mechanism in the electrophysiological sense. The only way a shock can influence the behavior of fibrillating cells is through the induced transmembrane potential. The result could be activation of a cell in the resting or relative refractory period. However one has to keep in mind that fibrillating cells do not behave in the same way as normal cells. Furthermore, the question is not simply what happens to individual cells but how the interaction of these cells is modified.
24.3.3 One-Dimensional Activation/Defibrillation Model
As noted above, one would like to know what electrophysiological effect is produced by the application of a stimulating current pulse (shock) on a group of fibrillating cardiac cells. This is a difficult problem to model. For one there is no model of the healthy ventricular membrane, let alone a fibrillating membrane that is satisfactory in all respects. Second it is also not clear what structural model is necessary that adequately reflects the electric interconnection of cells as well as the interstitial spaces necessary to reflect changes in ionic concentration (clefts). And finally there is the problem of handling the large three-dimensional structures (matrices) even with fast modern computers. A very much simpler problem was addressed by Plonsey, Barr, and Witkowski, 1991) in which the response of a one-dimensional cardiac strand to a current stimulus was considered. In this it was assumed that the membrane could be considered to be passive and under steady-state conditions. ((For shocks with a typical duration of 3-10 ms the steady-state assumption under subthreshold conditions appears to be valid (Cartee, 1991; Cartee and Plonsey, 1992).) In the aforementioned reference it is assumed that the heart can be considered as consisting of similar parallel fibers running from apex to base and that a uniform applied defibrillating current (also from apex to base) divides equally between such fibers. Consequently, the behavior of the heart can be examined through the behavior of any typical fiber. The response of a single uniform fiber to a current applied at its ends is considered in Section 9.4. Since the length of an equivalent cardiac fiber is perhaps 14 cm and since, for cardiac muscle, = 650 µm (Ideker et al. 1987), then the fiber is 215 in length. It is pointed out in Section 9.4 (see, e.g. Equations 9.11 and 10.12) that beyond around 5λ from the ends ΔVm is essentially zero and the axial current is uniform and divides in inverse proportion to the axial resistances. That is,
In the aforementioned reference it is assumed that the heart can be considered as consisting of similar parallel fibers running from apex to base and that a uniform applied defibrillating current (also from apex to base) divides equally between such fibers. Consequently, the behavior of the heart can be examined through the behavior of any typical fiber. The response of a single uniform fiber to a current applied at its ends is considered in Section 9.4. Since the length of an equivalent cardiac fiber is perhaps 14 cm and since, for cardiac muscle, = 650 µm (Ideker et al. 1987), then the fiber is 215 in length. It is pointed out in Section 9.4 (see, e.g. Equations 9.11 and 10.12) that beyond around 5λ from the ends ΔVm is essentially zero and the axial current is uniform and divides in inverse proportion to the axial resistances. That is,
 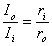 | (24.1) |
| where | Ii | = axial current inside the cell |
| Io | = axial current outside the cell | |
| ri | = axial intracellular resistance per unit length | |
| ro | = axial extracellular resistance per unit length |
 This means that perhaps 95% of the individual cells making up the cardiac fiber are unaffected by the stimulus! But this result depends on the equivalent fiber being uniform and neglects the intercellular junctions. If a single such junction is considered to link the intracellular space of adjoining cells (reflecting the gap-junctional resistance Rj), then each cell behaves identically and as described in Figure 24.4.
This means that perhaps 95% of the individual cells making up the cardiac fiber are unaffected by the stimulus! But this result depends on the equivalent fiber being uniform and neglects the intercellular junctions. If a single such junction is considered to link the intracellular space of adjoining cells (reflecting the gap-junctional resistance Rj), then each cell behaves identically and as described in Figure 24.4.
 In Figure 24.4, since the cell shown is replicated in a chain of around 1,200 such cells making up the total fiber, then voltages and currents must be periodic with a periodicity of one cell. Thus, for example, Ii entering at the left must equal Ii leaving at the right, since they are exactly one cell length apart. Now if the coupling resistances Rj were equal to zero, then the fiber would be uniform and the transmembrane current variation proportional to the second derivative of Vm as given by Equation 9.10. Consequently, it would also be essentially zero beyond 5λ of the ends. The effect of a finite Rj is to drive a small amount of current into and out of each cell (exactly the same must leave and enter since Ii must be periodic), and this movement is associated with a nonzero Vm in each cell. In fact, one can see that Rj causes a discontinuity in Φi just equal to the voltage drop, namely IiRj. This also represents a discontinuity in Vm. The presence of Rj forces some of the intracellular current out of the cell on the right half, but for the expected periodicity to be attained this current must enter the cell in the left half. Consequently both im and concomitantly Vm must be antisymmetric.
In Figure 24.4, since the cell shown is replicated in a chain of around 1,200 such cells making up the total fiber, then voltages and currents must be periodic with a periodicity of one cell. Thus, for example, Ii entering at the left must equal Ii leaving at the right, since they are exactly one cell length apart. Now if the coupling resistances Rj were equal to zero, then the fiber would be uniform and the transmembrane current variation proportional to the second derivative of Vm as given by Equation 9.10. Consequently, it would also be essentially zero beyond 5λ of the ends. The effect of a finite Rj is to drive a small amount of current into and out of each cell (exactly the same must leave and enter since Ii must be periodic), and this movement is associated with a nonzero Vm in each cell. In fact, one can see that Rj causes a discontinuity in Φi just equal to the voltage drop, namely IiRj. This also represents a discontinuity in Vm. The presence of Rj forces some of the intracellular current out of the cell on the right half, but for the expected periodicity to be attained this current must enter the cell in the left half. Consequently both im and concomitantly Vm must be antisymmetric.
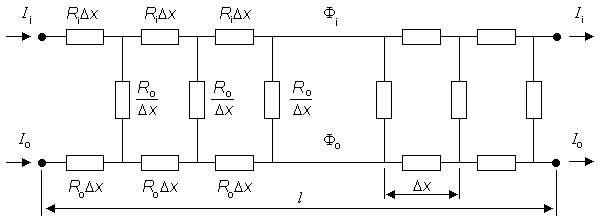
Fig. 24.4 Core-conductor electric network for a single cell that is a component of an equivalent single cardiac fiber. The cell is connected to its neighbors by an intracellular coupling resistance, Rj, at its ends. Steady-state subthreshold conditions are assumed.
 A mathematical description of Vm over the extent of the cell starts with the governing differential Equation 9.4. If we choose the origin at the center of the cell, then the solution to 9.4 should be chosen in terms of sinh(x/λ) to obtain the expected antisymmetry. From Equation 24.1, but including the junctional resistance's contribution to the net intracellular resistance per unit length, we have
A mathematical description of Vm over the extent of the cell starts with the governing differential Equation 9.4. If we choose the origin at the center of the cell, then the solution to 9.4 should be chosen in terms of sinh(x/λ) to obtain the expected antisymmetry. From Equation 24.1, but including the junctional resistance's contribution to the net intracellular resistance per unit length, we have
 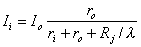 | (24.2) |
| where | Ii | = intracellular axial current inside the cell |
| Io | = extracellular axial current outside the cell | |
| ri | = intracellular axialresistance per unit length | |
| ro | = extracellular axialresistance per unit length | |
| Rj | = coupling resistance between cells | |
| l | = length of the cell |
 Consequently since the discontinuity at the ends of each cell requires that Vm(x = ± l/2) = IiRj, we get
Consequently since the discontinuity at the ends of each cell requires that Vm(x = ± l/2) = IiRj, we get
 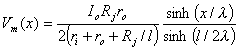 | (24.3) |
Allessie MA, Bonke FIM, Schopman FJG (1976): Circus movement in rabbit atrial muscle as a mechanism of tachycardia. II. Circ. Res. 39: 168-77.
Allessie MA, Bonke FIM, Schopman FJG (1977): Circus movement in rabbit atrial muscle as a mechanism of tachycardia. III The 'leading circle' concept: A new model of circus movement in cardiac tissue without involvement of an anatomical obstacle. Circ. Res. 41: 9-18.
Bourland JD, Mouchawar GA, Nyenhuis JA, Geddes LA, Foster KS, Jones JT, Graber GP (1990): Transchest magnetic (eddy-current) stimulation of the dog heart. Med. & Biol. Eng. & Comput. 28: 196-8.
Cartee L (1991): The cellular response of excitable tissue models to extracellular stimulation. Dept. Biomed. Eng., Duke Univ., Durham, pp. 158. (Ph.D. thesis)
Cartee LA, Plonsey R (1992): Active response of a one-dimensional cardiac model with gap junctions to extracellular stimulation. Med. & Biol. Eng. & Comput. 30:(4) 389-98.
Chen Peng-S, Wolf PD, Ideker RE (1991): Mechanism of cardiac defibrillation: A different point of view. Circulation 84: 913-9.
Greatbatch W, Seligman LJ (1988): Pacemakers. In Encyclopedia of Medical Devices and Instrumentation, ed. JG Webster, pp. 2175-203, John Wiley & Son, New York.
Ideker RE, Chen P-S, Shibata N, Colavita PG, Wharton JM (1987): Current concepts of the mechanisms of ventricular defibrillation. In Nonpharmacological Theory of Tachyarrhythmias, ed. G Breithardt, M Borggrefe, DP Zipes, pp. 449-64, Futura Pub. Co., Mount Kisco, New York.
Irwin DD, Rush S, Evering R, Lepeshkin E, Montgomery DB, Weggel RJ (1970): Stimulation of cardiac muscle by a time-varying magnetic field. IEEE Trans. Magn. Mag-6:(2) 321-2.
Janse MJ, Van Capelle FJL, Morsink H, Kléber AG, Wilms-Schopman FJG, Cardinal R, Naumann d'Alnoncourt C, Durrer D (1980): Flow of 'injury' current and patterns of excitation during early ventricular arrhythmias in acute regional myocardial ischemia in isolated porcine and canine hearts. Circ. Res. 47: 151-65.
Kerber RE (1990): External direct current defibrillation and cardioversion. In Cardiac Electrophysiology, ed. DP Zipes, J Jalife, pp. 954-9, W.B. Saunders, Philadelphia.
Kubota H, Yamaguchi M, Yamamoto I (1993): Development of magnetic defibrillator - Distribution of eddy-currents by stimulating coils. J. Jpn. Biomagn. Bioelectromagn. Soc. 6: 78-81.
Mines GR (1913): On dynamic equilibrium in the heart. J. Physiol. (Lond.) 46: 349-82.
Mouchawar GA, Bourland JD, Nyenhuis JA, Geddes LA, Foster KS, Jones JT, Graber GP (1992): Closed-chest cardiac stimulation with a pulsed magnetic field. Med. & Biol. Eng. & Comput. 30:(2) 162-8.
Plonsey R, Barr RC, Witkowski FX (1991): One-dimensional model of cardiac defibrillation. Med. & Biol. Eng. & Comput. 29:(5) 465-9.
Spach MS, Dolber PC (1985): The relation between discontinuous propagation in anisotropic cardiac muscle and the 'vulnerable period' of reentry. In Cardiac Electrophysiology and Arrhythmias, ed. DP Zipes, J Jalife, pp. 241-52, Grune and Stratton, Orlando.
Witkowski FX, Penkoske PA, Plonsey R (1990): Mechanism of cardiac defibrillation in open-chest dogs with unipolar DC-coupled simultaneous activation and shock potential recordings. Circulation 82:(1) 244-60.
 In Equation 24.3 the factor of 2 takes into account the positive and negative excursion of the expression, whereas the factor sinh(l/2λ) is a constant that is required by the boundary condition. An estimate of the applied current in the equivalent fiber, Io, can be made by starting with the total current applied by the defibrillator. From the model we assume that the fraction associated with the equivalent fiber is the cross-section of the fiber and its associated interstitial space divided by the cross-section of the entire heart. Using typical physiological values, one obtains cellular depolarizations of ±(6-30) mV (Plonsey, Barr, and Witkowski, 1991), which is in a range that could certainly affect a cell's electrophysiological behavior.
In Equation 24.3 the factor of 2 takes into account the positive and negative excursion of the expression, whereas the factor sinh(l/2λ) is a constant that is required by the boundary condition. An estimate of the applied current in the equivalent fiber, Io, can be made by starting with the total current applied by the defibrillator. From the model we assume that the fraction associated with the equivalent fiber is the cross-section of the fiber and its associated interstitial space divided by the cross-section of the entire heart. Using typical physiological values, one obtains cellular depolarizations of ±(6-30) mV (Plonsey, Barr, and Witkowski, 1991), which is in a range that could certainly affect a cell's electrophysiological behavior.
 The above examination of the effect of the intracellular junctional resistance in producing a Vm from a uniform stimulating electric field demonstrates that this effect can arise from any interruption in tissue uniformity. Other histological non-uniformities can also be important in "converting" a uniform applied electric field into an induced transmembrane potential. Recent studies suggest that such a role may be performed by the fiber rotation known to take place in the myocardium.
The above examination of the effect of the intracellular junctional resistance in producing a Vm from a uniform stimulating electric field demonstrates that this effect can arise from any interruption in tissue uniformity. Other histological non-uniformities can also be important in "converting" a uniform applied electric field into an induced transmembrane potential. Recent studies suggest that such a role may be performed by the fiber rotation known to take place in the myocardium.
24.4 DEFIBRILLATOR DEVICES
The high amount of energy that must be delivered is achieved with conventional defibrillators by first charging a large capacitance and then discharging it in a damped RLC circuit. In certain designs the pulse is terminated by short-circuiting the capacitance, resulting in a trapezoidal-like wave. Both the damped sine-wave and the trapezoidal waveform are generally used, and there is little evidence that one is better than the other. (Greatbatch and Seligman, 1988; Kerber, 1990)
 Defibrillators are calibrated by the energy discharged into a 50 Ω load. This measure of defibrillation strength competes with the more recent understanding that defibrillation is achieved by the current-flow field, as discussed above. Strength-duration curves are available for applied energy, charge, and current, based on animal studies in which these quantities are varied. For durations greater than 1 ms the current magnitude required for defibrillation remains about the same (suggesting a chronaxie of perhaps 0.5 ms).
Defibrillators are calibrated by the energy discharged into a 50 Ω load. This measure of defibrillation strength competes with the more recent understanding that defibrillation is achieved by the current-flow field, as discussed above. Strength-duration curves are available for applied energy, charge, and current, based on animal studies in which these quantities are varied. For durations greater than 1 ms the current magnitude required for defibrillation remains about the same (suggesting a chronaxie of perhaps 0.5 ms).
 Transchest defibrillator electrodes have diameters in the range of 8-13 cm. Electrodes manufactured for direct application to the heart (e.g., during a surgical procedure) are smaller (4-8 cm) in diameter. Large-diameter electrodes are used in an attempt to achieve a uniform field within the heart and also to avoid high current densities that could burn the skin. The total dry transchest impedance is found to be 25-150 Ω, while the transcardiac impedance is typically 20-40 Ω. (The transchest impedance depends on the electrode-skin impedance and, with the use of an appropriate gel, will be about 50 Ω). Transchest defibrillation energy is in the range of 200-360 joules. It needs a current of 24 A, 20 ms, and a voltage of 5 kV, monophasic, or 2 kV, biphasic. An inadequate current for defibrillation can result from the selection of a low energy level while being unaware of a high transchest impedance (inadequate skin preparation). Some devices first sense this impedance and then choose the energy level to ensure an adequate current.
Transchest defibrillator electrodes have diameters in the range of 8-13 cm. Electrodes manufactured for direct application to the heart (e.g., during a surgical procedure) are smaller (4-8 cm) in diameter. Large-diameter electrodes are used in an attempt to achieve a uniform field within the heart and also to avoid high current densities that could burn the skin. The total dry transchest impedance is found to be 25-150 Ω, while the transcardiac impedance is typically 20-40 Ω. (The transchest impedance depends on the electrode-skin impedance and, with the use of an appropriate gel, will be about 50 Ω). Transchest defibrillation energy is in the range of 200-360 joules. It needs a current of 24 A, 20 ms, and a voltage of 5 kV, monophasic, or 2 kV, biphasic. An inadequate current for defibrillation can result from the selection of a low energy level while being unaware of a high transchest impedance (inadequate skin preparation). Some devices first sense this impedance and then choose the energy level to ensure an adequate current.
 Totally implanted defibrillators have been increasingly used, as discussed in the earlier section on cardiac pacemakers. Because they connect directly with the heart, a threshold current of 1-2 A can be achieved at lower voltages and energies. Assuming a transcardiac impedance of 20 Ω requires an applied voltage of around 30 V and an energy of perhaps 30 J.
Totally implanted defibrillators have been increasingly used, as discussed in the earlier section on cardiac pacemakers. Because they connect directly with the heart, a threshold current of 1-2 A can be achieved at lower voltages and energies. Assuming a transcardiac impedance of 20 Ω requires an applied voltage of around 30 V and an energy of perhaps 30 J.
 Experimental work is also in progress for developing a cardiac defibrillator which uses a magnetic field to stimulate the cardiac muscle (Bourland et al., 1990; Irwin et al., 1970; Kubota et al., 1993; Mouchawar et al., 1992)..
Experimental work is also in progress for developing a cardiac defibrillator which uses a magnetic field to stimulate the cardiac muscle (Bourland et al., 1990; Irwin et al., 1970; Kubota et al., 1993; Mouchawar et al., 1992)..
REFERENCES



